Complex Step Differentiation
Complex step differentiation is a method for estimating the derivative of a function \(f(x)\) using the equation:
- \(f'(x) \approx \frac{ Im[f(x + ih)] }{h}\)
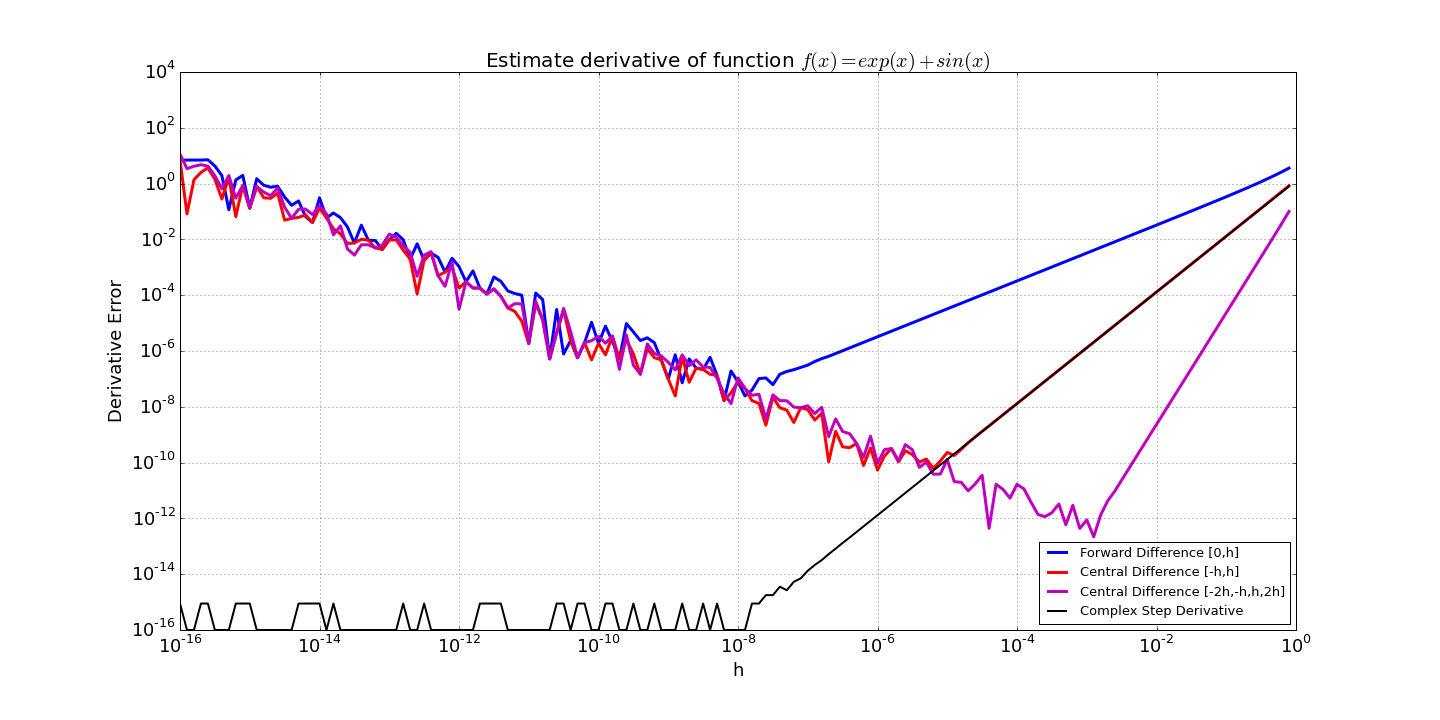
Unlike finite-difference formulas, the complex-step formula does not suffer from roundoff errors due to subtraction, so a very small value of the step size \(h\) can be used, producing a much more accurate derivative. The example shown below is for the function: \(f(x) = e^x + \sin(x)\). The derivative error is compared to three finite-difference formulas:
- \(f'(x) \approx \frac{f(x+h) - f(x)}{h}\) (Two-point forward difference)
- \(f'(x) \approx \frac{f(x+h) - f(x-h)}{2h}\) (Two-point central difference)
- \(f'(x) \approx \frac{f(x-2h) -8 f(x-h) + 8 f(x+h) - f(x+2h) }{12 h}\) (Four-point central difference)
For large values of \(h\), truncation error dominates. The finite-difference error decreases as \(h\) is decreased, until roundoff error begins to dominate (around \(10^{-8}\) for the forward difference, \(10^{-5}\) for the 2-point central difference, and \(10^{-3}\) for the 4-point central difference). The complex-step estimate, however, can produce a derivative estimate to machine precision for any value of \(h < 10^{-8}\).
See also
- J.R.R.A. Martins, I.M. Kroo, J.J. Alonso, "An Automated Method for Sensitivity Analysis using Complex Variables", AIAA-2000-0689.
- complex_step.f90 in the Fortran Astrodynamics Toolkit.