C++ vs Fortran (Part 3)
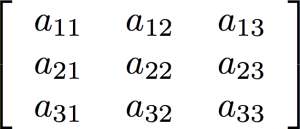
Built-in high-level support for arrays (vectors and matrices) using a very clean syntax is one of the areas where Fortran really shines as a programming language for engineering and scientific simulations. As an example, consider matrix multiplication. Say we have an M x K matrix A, a K x N matrix B, and we want to multiply them to get the M x N matrix AB. Here's the code to do this in Fortran:
AB = matmul(A,B)
Now, here's how to do the same thing in C or C++ (without resorting to library calls) [1]:
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
AB[i][j]=0;
for (int k = 0; k < K; k++) {
AB[i][j] += A[i][k] * B[k][j];
}
}
}
MATMUL is, of course, Fortran's built-in matrix multiplication function. It was added to the language as part of the Fortran 90/95 standards which dramatically upgraded the language's array-handling facilities. Later standards also added additional array features, and Fortran currently contains a wide range of intrinsic array functions:
| Routine | Description |
|---|---|
| ALL | True if all values are true |
| ALLOCATED | Array allocation status |
| ANY | True if any value is true |
| COUNT | Number of true elements in an array |
| CSHIFT | Circular shift |
| DOT_PRODUCT | Dot product of two rank-one arrays |
| EOSHIFT | End-off shift |
| FINDLOC | Location of a specified value |
| IPARITY | Exclusive or of array elements |
| IS_CONTIGUOUS | Test contiguity of an array |
| LBOUND | Lower dimension bounds of an array |
| MATMUL | Matrix multiplication |
| MAXLOC | Location of a maximum value in an array |
| MAXVAL | Maximum value in an array |
| MERGE | Merge under mask |
| MINLOC | Location of a minimum value in an array |
| MINVAL | Minimum value in an array |
| NORM2 | L2 norm of an array |
| PACK | Pack an array into an array of rank one under a mask |
| PARITY | True if number of elements in odd |
| PRODUCT | Product of array elements |
| RESHAPE | Reshape an array |
| SHAPE | Shape of an array or scalar |
| SIZE | Total number of elements in an array |
| SPREAD | Replicates array by adding a dimension |
| SUM | Sum of array elements |
| TRANSPOSE | Transpose of an array of rank two |
| UBOUND | Upper dimension bounds of an array |
| UNPACK | Unpack an array of rank one into an array under a mask |
As an example, here is how to sum all the positive values in a matrix:
b = sum(A, mask=(A>0.0))
In addition to the array-handling functions, we can also use various other language features to make it easier to work with arrays. For example, say we wanted to convert all the negative elements of a matrix to zero:
where (A<0.0) A = 0.0
Or, say we want to compute the dot product of the 1st and 3rd columns of a matrix:
d = dot_product(A(:,1),A(:,3))
Or, replace every element of a matrix with its sin():
A = sin(A)
That last one is an example of an intrinsic ELEMENTAL function, which is one that can operate on scalars or arrays of any rank. The assignment is done for each element of the array (and can potentially be vectored by the compiler). We can create our own ELEMENTAL functions like so:
elemental function cubic(a,b,c) result(d)
real(wp),intent(in) :: a,b,c
real(wp) :: d
d = a + b**2 + c**3
end function cubic
Note that the inputs and output of this function are scalars. However, since it is ELEMENTAL, it can also be used for arrays like so:
real(wp) :: aa,bb,cc,dd
real(wp),dimension(10,10,10) :: a,b,c,d
!...
dd = cubic(aa,bb,cc) ! works on these
d = cubic(a,b,c) ! also works on these
The array-handling features of Fortran make scientific and engineering programming simpler and less error prone, since the code can be closer to the mathematical expressions, as well as making vectorization by the compiler easier [2]. Here is an example from the Fortran Astrodynamics Toolkit, a vector projection function:
pure function vector_projection(a,b) result(c)
implicit none
real(wp),dimension(:),intent(in) :: a
!! the original vector
real(wp),dimension(size(a)),intent(in) :: b
!! the vector to project on to
real(wp),dimension(size(a)) :: c
!! the projection of a onto b
if (all(a==0.0_wp)) then
c = 0.0_wp
else
c = a * dot_product(a,b) / dot_product(a,a)
end if
end function vector_projection
Line 15 is the vector projection formula, written very close to the mathematical notation. The function also works for any size vector. A similar function in C++ would be something like this:
inline std::array<double,3>
vector_projection(const std::array<double,3>& a,
const std::array<double,3>& b)
{
if (a[0]==0.0 & a[1]==0.0 & a[2]==0.0){
std::array<double,3> p = {0.0, 0.0, 0.0};
return p;
}
else{
double aa = a[0]*a[0]+a[1]*a[1]+a[2]*a[2];
double ab = a[0]*b[0]+a[1]*b[1]+a[2]*b[2];
double abaa = ab / aa;
std::array<double,3>
p = {a[0]*abaa,a[1]*abaa,a[2]*abaa};
return p;
}
}
Of course, like anything, there are many other ways to do this in C++ (I'm using C++11 standard library arrays just for fun). Note that the above function only works for vectors with 3 elements. It's left as an exercise for the reader to write one that works for any size vectors like the Fortran one (full disclosure: I mainly just Stack Overflow my way through writing C++ code!) C++'s version of dot_product seems to have a lot more inputs for you to figure out though:
double ab = std::inner_product(a.begin(),a.end(),b.begin(),0.0);
In any event, any sane person using C++ for scientific and engineering work should be using a third-party array library, of which there are many (e.g., Boost, EIGEN, Armadillo, Blitz++), rather than rolling your own like we do at NASA.
References
- Walkthrough: Matrix Multiplication [MSDN]
- M. Metcalf, The Seven Ages of Fortran, Journal of Computer Science and Technology, Vol. 11 No. 1, April 2011.
- My Corner of the World: C++ vs Fortran, September 07, 2011