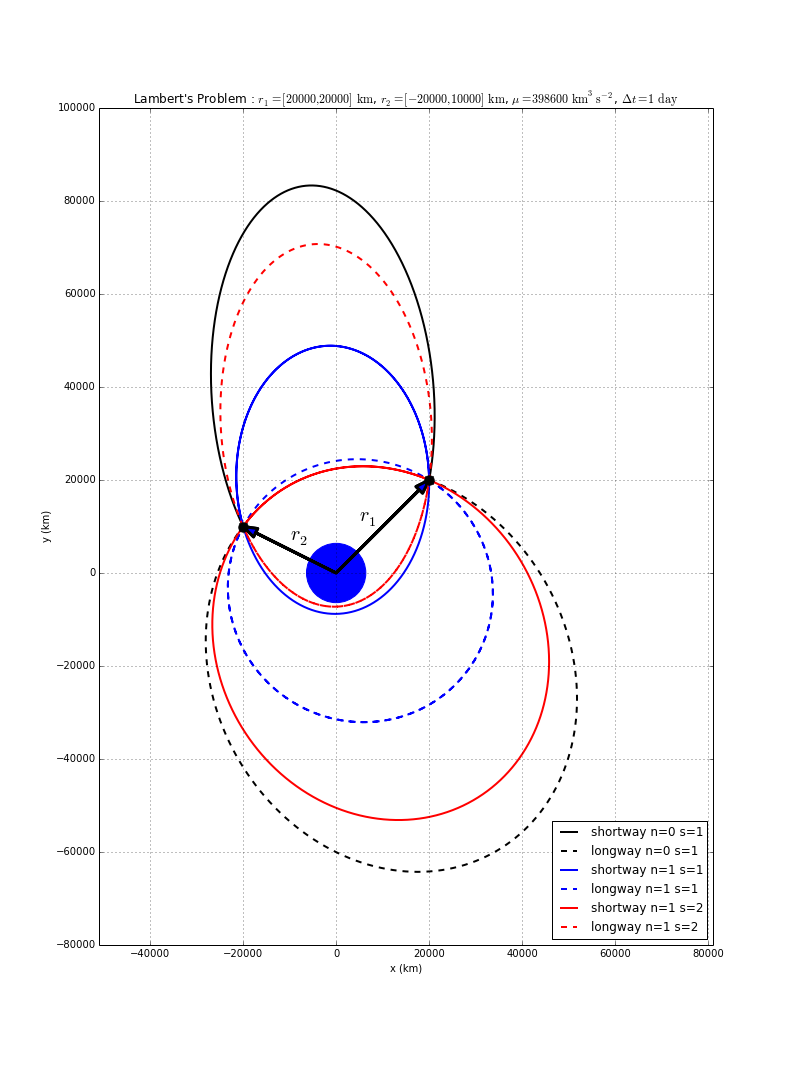
Lambert's Problem
Lambert's problem is to solve for the orbit transfer that connects two position vectors in a given time of flight. It is one of the basic problems of orbital mechanics, and was solved by Swiss mathematician Johann Heinrich Lambert.
A standard Fortran 77 implementation of Lambert's problem was presented by Gooding [1]. A modern update to this implementation is included in the Fortran Astrodynamics Toolkit, which also includes a newer algorithm from Izzo [2].
There can be multiple solutions to Lambert's problem, which are classified by:
- Direction of travel (i.e., a "short" way or "long" way transfer).
- Number of complete revolutions (N=0,1,...). For longer flight times, solutions exist for larger values of N.
- Solution number (S=1 or S=2). The multi-rev cases can have two solutions each.
In the example shown here, there are 6 possible solutions:
References
- R.H, Gooding. "A procedure for the solution of Lambert's orbital boundary-value problem", Celestial Mechanics and Dynamical Astronomy, Vol. 48, No. 2, 1990.
- D. Izzo, "Revisiting Lambert’s problem", Celestial Mechanics and Dynamical Astronomy, Oct. 2014.