Low Lunar Orbit Maintenance
The lunar gravity field is bumpy. Thus a spacecraft in a low lunar orbit for an extended period of time must perform periodic correction maneuvers or the orbit eventually becomes unstable and can crash into the Moon. When the Orion spacecraft was being designed during the late Constellation Program, the requirements of global surface access sortie missions, six-month polar outpost missions, anytime aborts, and autonomous operation of the vehicle while the crew was on the surface, required lots of analysis to figure out how to make the architecture work. And then the program was canceled.
The reference low-lunar orbit maintenance algorithm we used during Constellation was fairly simple. Orion initially inserted into a retrograde circular parking orbit with a 100 km altitude. During orbit propagation, if the altitude was reduced by a specified deadband altitude (say 10 km) the vehicle would perform a periapsis raise maneuver at the next apoapsis to bring the periapsis back up to 100 km. The apoapsis radius was not controlled, and indeed all the other orbital elements were also allowed to float. This would continue until the crew was ready to return (on the Altiar lander ascent stage), at which point Orion would circularize the orbit and perform a plane change to allow Altair to perform an in-plane ascent.
The \(\Delta v\) maneuver to perform at apoapsis of an orbit with a periapsis radius \(r_{pi}\) and apoapsis radius \(r_{ai}\), to target a periapsis radius \(r_{pf}\) can be computed by:
- Initial apoapsis velocity: \(v_{ai} = \sqrt{ 2 \mu \frac{r_{pi}}{r_{ai} (r_{ai}+r_{pi})} }\)
- Final apoapsis velocity: \(v_{af} = \sqrt{ 2 \mu \frac{r_{pf}}{r_{ai} (r_{ai}+r_{pf})} }\)
- Maneuver magnitude: \(\Delta v = v_{af} - v_{ai}\)
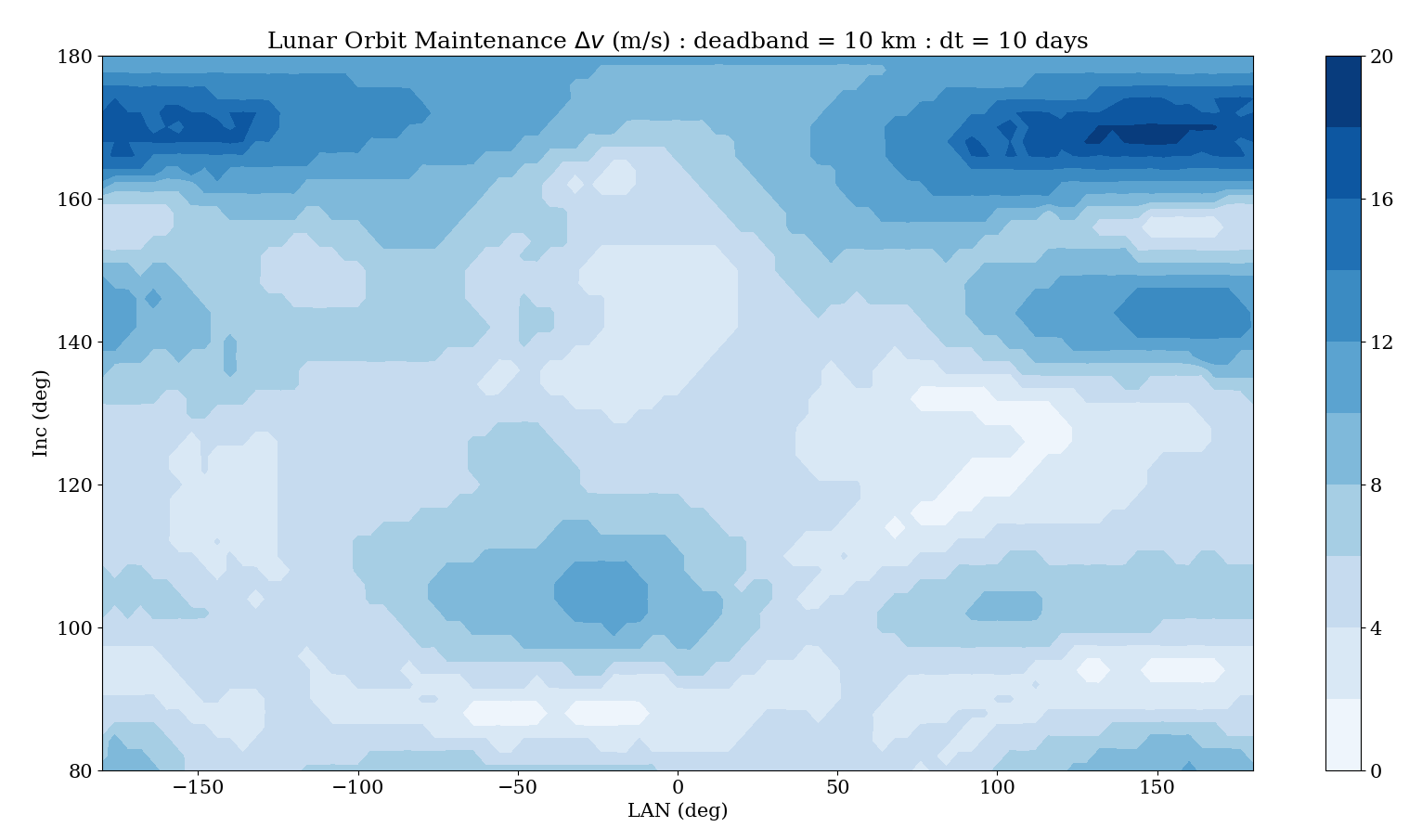
We can implement this method using the Fortran Astrodynamics Toolkit fairly easily. We also need an integrator with an event finding capability (we can use DDEABM, a variable step size variable order Adams method). We propagate from the initial insertion state until the deadband altitude is violated, then propagate to the next apoapsis where the periapsis raise maneuver is performed, then repeat as necessary. The code implementing this scheme can be found on GitHub here. For the force model, we are using a 20 x 20 GRAIL geopotential model of the Moon (not available during Constellation, when we used the Lunar Prospector derived LP150Q model). A contour plot of the results for 100 km retrograde orbits with a 10 km altitude deadband and 10 days of propagation time are shown below. Each maneuver ends up being about 2 m/s for this example, and the bumpiness of the gravity field is evident. Some insertion orbits require no maneuvers, while others require about 18 m/s over the 10 day period.
See also
- J. Williams, S. M. Stewart, D. E. Lee, E. C. Davis, G. E. Condon, J. S. Senent. "The Mission Assessment Post Processor (MAPP): A New Tool for Performance Evaluation of Human Lunar Missions", 20th AAS/AIAA Space Flight Mechanics Meeting, 14-17 February 2010, San Diego, CA.
- F.G. Lemoine, S. Goossens, T.J. Sabaka, et al. GRGM900C: A degree 900 lunar gravity model from GRAIL primary and extended mission data. Geophysical Research Letters. 2014;41(10):3382-3389.
- R. B. Roncoli, Lunar Constants and Models Document, JPL D-32296, Sept 23, 2005.
- M. Beckman, L. Rivers, Stationkeeping for the Lunar Reconnaissance Orbiter (LRO), 20th International Symposium on Space Flight Dynamics, 24-28 Sep. 2007.
