Lagrange Interpolating Polynomials
A simple Fortran implementation of interpolation by Lagrange polynomials is given below. Though named after Joseph-Louis Lagrange, the formula was first discovered by English mathematician Edward Waring.
subroutine lagrange_interpolation(xx,yy,x,y)
!
! Interpolate xx=[x1,x2,...xn]
! yy=[f(x1),f(x2),...,f(xn)]
! Using Lagrange polynomial P(x)
! Returns y = P(x)
!
use,intrinsic :: iso_fortran_env, wp => real64
implicit none
real(wp),dimension(:),intent(in) :: xx
real(wp),dimension(:),intent(in) :: yy
real(wp),intent(in) :: x
real(wp),intent(out) :: y
!local variables:
integer :: j,k,n,m
real(wp) :: p
!check number of points:
n = size(xx)
m = size(yy)
if (n/=m) error stop &
'Error: vectors must be the same size.'
!sum each of the Pj(x) terms:
y = 0.0_wp
do j=1,n
!compute Pj(x):
p = yy(j)
do k=1,n
if (k/=j) p = p * (x-xx(k)) / (xx(j)-xx(k))
end do
y = y + p
end do
end subroutine lagrange_interpolation
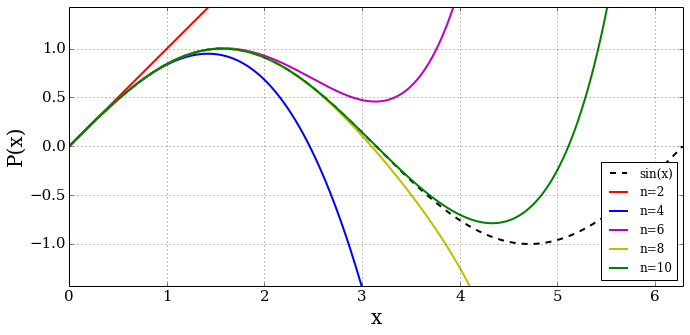
Examples of interpolating polynomials for the \(\sin(x)\) function are shown here for different numbers of points \(x=[0.0, 0.01]\), \(x=[0.0, 0.01, 0.02]\), etc.
References
- Lagrange Interpolating Polynomial [Wolfram Mathworld]
- E. Waring, "Problems Concerning Interpolations", Philosophical Transactions of the Royal Society of London, Vol. 69 (1779), p. 59-67.