Refactoring
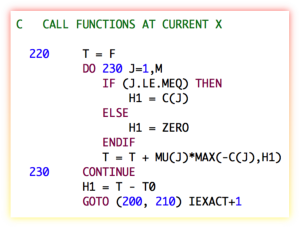
SLSQP [1-2] is a sequential least squares constrained optimization algorithm written by Dieter Kraft in the 1980s. Today, it forms part of the Python pyOpt package for solving nonlinear constrained optimization problems. It was written in FORTRAN 77, and is filled with such ancient horrors like arithmetic IF statements, GOTO statements (even computed and assigned GOTO statements), statement functions, etc. It also assumes the implicit saving of variables in the LINMIN subroutine (which is totally non-standard, but was done by some early compilers), and in some instances assumes that variables are initialized with a zero value (also non-standard, but also done by some compilers). It has an old-fashioned "reverse communication" style interface, with generous use of "WORK" arrays passed around using assumed-size dummy arguments. The pyOpt users don't seem to mind all this, since they are calling it from a Python wrapper, and I guess it works fine (for now).
I don't know if anyone has ever tried to refactor this into modern Fortran with a good object-oriented interface. It seems like it would be a good idea. I've been toying with it for a while. It is always an interesting process to refactor old Fortran code. The fixed-form to free-form conversion can usually be done fairly easily with an automated script, but untangling the spaghetti can be a bit harder. Consider the following code snipet from the subroutine HFTI:
C DETERMINE PSEUDORANK
DO 90 j=1,ldiag
90 IF(ABS(a(j,j)).LE.tau) GOTO 100
k=ldiag
GOTO 110
100 k=j-1
110 kp1=k+1
A modern version that performs the exact same calculation is:
!determine pseudorank:
do j=1,ldiag
if (abs(a(j,j))<=tau) exit
end do
k=j-1
kp1=j
As you can see, no line numbers or GOTO statements are required. The new version even eliminates one assignment and one addition operation. Note that the refactored version depends on the fact that the index of the DO loop, if it completes the loop (i.e., if the exit statement is not triggered), will have a value of ldiag+1. This behavior has been part of the Fortran standard for some time (perhaps it was not when this routine was written?).
There is also a C translation of SLSQP available, which fixes some of the issues in the original code. Their version of the above code snippet is a pretty straightforward translation of the FORTRAN 77 version, except with all the ugliness of C on full display (a[j + j * a_dim1], seriously?):
/* DETERMINE PSEUDORANK */
i__2 = ldiag;
for (j = 1; j <= i__2; ++j) {
/* L90: */
if ((d__1 = a[j + j * a_dim1], fabs(d__1)) <= *tau) {
goto L100;
}
}
k = ldiag;
goto L110;
L100:
k = j - 1;
L110:
kp1 = k + 1;
See Also
- Dieter Kraft, "A Software Package for Sequential Quadratic Programming", DFVLR-FB 88-28, 1988.
- Dieter Kraft, "Algorithm 733: TOMP–Fortran Modules for Optimal Control Calculations," ACM Transactions on Mathematical Software, Vol. 20, No. 3, p. 262-281 (1994).
- John Burkardt, LAWSON Least Squares Routines, 21 October 2008. [Fortran 90 versions of the least squares routines used in SLSQP].