Degenerate Conic

Refactoring (Part 2)

I'm working on a modern Fortran version of the simulated annealing optimization algorithm, using this code as a starting point. There is a Fortran 90 version here, but this seems to be mostly just a straightforward conversion of the original code to free-form source formatting. I have in mind a more thorough modernization and the addition of some new features that I need.

Refactoring old Fortran code is always fun. Consider the following snippet:

C  Check termination criteria.
      QUIT = .FALSE.
      FSTAR(1) = F
      IF ((FOPT - FSTAR(1)) .LE. EPS) QUIT = .TRUE.
      DO 410, I = 1, NEPS
        IF (ABS(F - FSTAR(I)) .GT. EPS) QUIT = .FALSE.
410   CONTINUE

This can be greatly simplified to:

! check termination criteria.
fstar(1) = f
quit = ((fopt-f)<=eps) .and. (all(abs(f-fstar)<=eps)

Note that we are using some of the vector features of modern Fortran to remove the loop. Consider also this function in the original code:

      FUNCTION  EXPREP(RDUM)
C  This function replaces exp to avoid under- and overflows and is
C  designed for IBM 370 type machines. It may be necessary to modify
C  it for other machines. Note that the maximum and minimum values of
C  EXPREP are such that they has no effect on the algorithm.

      DOUBLE PRECISION  RDUM, EXPREP

      IF (RDUM .GT. 174.) THEN
         EXPREP = 3.69D+75
      ELSE IF (RDUM .LT. -180.) THEN
         EXPREP = 0.0
      ELSE
         EXPREP = EXP(RDUM)
      END IF

      RETURN
      END

It is somewhat disturbing that the comments mention IBM 370 machines. This routine is unchanged in the f90 version. However, these numeric values are no longer correct for modern hardware. Using modern Fortran, we can write a totally portable version of this routine like so:

pure function exprep(x) result(f)

use, intrinsic :: ieee_exceptions

implicit none

real(dp), intent(in) :: x
real(dp) :: f

logical,dimension(2) :: flags
type(ieee_flag_type),parameter,dimension(2) :: out_of_range = [ieee_overflow,ieee_underflow]

call ieee_set_halting_mode(out_of_range,.false.)

f = exp(x)

call ieee_get_flag(out_of_range,flags)
if (any(flags)) then
  call ieee_set_flag(out_of_range,.false.)
  if (flags(1)) then
    f = huge(1.0_dp)
  else
    f = 0.0_dp
  end if
end if

end function exprep

This new version is entirely portable and works for any real kind. It contains no magic numbers and uses the intrinsic IEEE exceptions module of modern Fortran to protect against overflow and underflow, and the huge() intrinsic to return the largest real(dp) number.

So, stay tuned...

See also

• S. Kirkpatrick, C. D. Gelatt Jr., M. P. Vecchi, "Optimization by Simulated Annealing", Science 13 May 1983, Vol. 220, Issue 4598, pp. 671-680
• W. L. Goffe, SIMANN: A Global Optimization Algorithm using Simulated Annealing, Studies in Nonlinear Dynamics & Econometrics, De Gruyter, vol. 1(3), pages 1-9, October 1996.
• Original simann.f source code [Netlib]

SLATEC

The SLATEC Common Mathematical Library (CML) is written in FORTRAN 77 and contains over 1400 general purpose mathematical and statistical routines. SLATEC is an acronym for the "Sandia, Los Alamos, Air Force Weapons Laboratory Technical Exchange Committee", an organization formed in 1974 by the computer centers of these organizations. In 1977, it was decided to build a FORTRAN library to provide portable, non-proprietary, mathematical software for member sites' supercomputers. Version 1.0 of the CML was released in April 1982.

An example SLATEC routine is shown below, which computes the inverse hyperbolic cosine:

*DECK ACOSH
    FUNCTION ACOSH (X)
C***BEGIN PROLOGUE ACOSH
C***PURPOSE Compute the arc hyperbolic cosine.
C***LIBRARY SLATEC (FNLIB)
C***CATEGORY C4C
C***TYPE SINGLE PRECISION (ACOSH-S, DACOSH-D, CACOSH-C)
C***KEYWORDS ACOSH, ARC HYPERBOLIC COSINE, ELEMENTARY FUNCTIONS, FNLIB,
C INVERSE HYPERBOLIC COSINE
C***AUTHOR Fullerton, W., (LANL)
C***DESCRIPTION
C
C ACOSH(X) computes the arc hyperbolic cosine of X.
C
C***REFERENCES (NONE)
C***ROUTINES CALLED R1MACH, XERMSG
C***REVISION HISTORY (YYMMDD)
C 770401 DATE WRITTEN
C 890531 Changed all specific intrinsics to generic. (WRB)
C 890531 REVISION DATE from Version 3.2
C 891214 Prologue converted to Version 4.0 format. (BAB)
C 900315 CALLs to XERROR changed to CALLs to XERMSG. (THJ)
C 900326 Removed duplicate information from DESCRIPTION section.
C (WRB)
C***END PROLOGUE ACOSH
    SAVE ALN2,XMAX
    DATA ALN2 / 0.6931471805 5994530942E0/
    DATA XMAX /0./
C***FIRST EXECUTABLE STATEMENT ACOSH
    IF (XMAX.EQ.0.) XMAX = 1.0/SQRT(R1MACH(3))
C
    IF (X .LT. 1.0) CALL XERMSG ('SLATEC', 'ACOSH', 'X LESS THAN 1',
  + 1, 2)
C
    IF (X.LT.XMAX) ACOSH = LOG (X + SQRT(X*X-1.0))
    IF (X.GE.XMAX) ACOSH = ALN2 + LOG(X)
C
    RETURN
    END

Of course, this routine is full of nonsense from the point of view of a modern Fortran programmer (fixed-form source, implicitly typed variables, SAVE and DATA statements, constants computed at run time rather than compile time, hard-coding of the numeric value of ln(2), etc.). And you don't even want to know what's happening in the R1MACH() function. A modern version would look something like this:

pure elemental function acosh(x) result(acoshx)

!! arc hyperbolic cosine

use iso_fortran_env, only: wp => real64

implicit none

real(wp),intent(in) :: x
real(wp) :: acoshx

real(wp),parameter :: aln2 = &
    log(2.0_wp)
real(wp),parameter :: r1mach3 = &
    real(radix(1.0_wp),wp)**(-digits(1.0_wp)) !! largest relative spacing
real(wp),parameter :: xmax = &
    1.0_wp/sqrt(r1mach3)

if ( x<1.0_wp ) then
    error stop 'slatec : acosh : x less than 1'
else
    if ( x<xmax ) then
        acoshx = log(x + sqrt(x*x - 1.0_wp))
    else
        acoshx = aln2 + log(x)
    end if
end if

end function acosh

Of course, the point is moot, since ACOSH() is now an intrinsic function in Fortran 2008, so we don't need either of these anymore. Unfortunately, like many great Fortran codes, SLATEC has been frozen in amber since the early 1990's. It does contain a great many gems, however, and any deficiencies in the original Fortran 77 code can be easily remedied using modern Fortran standards. See also, for example, my own DDEABM project, which is a complete refactoring and upgrade of the Adams-Bashforth-Moulton ODE solver from SLATEC.

The GNU Scientific Library was started in 1996 to be a "modern version of SLATEC". Of course, rather than refactoring into modern Fortran (Fortran 90 had been published several years earlier, but I believe it was some time before a free compiler was available) they decided to start over in C. There's now even a Fortran interface to GSL (so now we can use a Fortran wrapper to call a C function that replaced a Fortran function that worked perfectly well to begin with!) The original SLATEC was a public domain work of the US government, and so can be used without restrictions in free or proprietary applications, but GSL is of course, GPL, so you're out of luck if you are unable to accept the ~~restrictions~~ (I mean freedom) of that license.

Note that John Burkardt has produced a version of SLATEC translated to free-form source. The license for this modified version is unclear. Many of his other codes are LGPL (still more restrictive than the original public domain codes). It's not a full refactoring, either. The codes still contain non-standard extensions and obsolescent and now-unnecessary features such as COMMON blocks. What we really need is a full modern refactoring of SLATEC (and other unmaintained codes like the NIST CMLIB and NSWC, etc.)

References

1. Fong, Kirby W., Jefferson, Thomas H., Suyehiro, Tokihiko, Walton, Lee, "Guide to the SLATEC Common Mathematical Library", July 1993.
2. SLATEC source code at Netlib.

Refactoring

SLSQP [1-2] is a sequential least squares constrained optimization algorithm written by Dieter Kraft in the 1980s. Today, it forms part of the Python pyOpt package for solving nonlinear constrained optimization problems. It was written in FORTRAN 77, and is filled with such ancient horrors like arithmetic IF statements, GOTO statements (even computed and assigned GOTO statements), statement functions, etc. It also assumes the implicit saving of variables in the LINMIN subroutine (which is totally non-standard, but was done by some early compilers), and in some instances assumes that variables are initialized with a zero value (also non-standard, but also done by some compilers). It has an old-fashioned "reverse communication" style interface, with generous use of "WORK" arrays passed around using assumed-size dummy arguments. The pyOpt users don't seem to mind all this, since they are calling it from a Python wrapper, and I guess it works fine (for now).

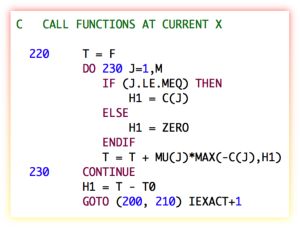
I don't know if anyone has ever tried to refactor this into modern Fortran with a good object-oriented interface. It seems like it would be a good idea. I've been toying with it for a while. It is always an interesting process to refactor old Fortran code. The fixed-form to free-form conversion can usually be done fairly easily with an automated script, but untangling the spaghetti can be a bit harder. Consider the following code snipet from the subroutine HFTI:

C DETERMINE PSEUDORANK
    DO 90 j=1,ldiag
90  IF(ABS(a(j,j)).LE.tau) GOTO 100
    k=ldiag
    GOTO 110
100 k=j-1
110 kp1=k+1

A modern version that performs the exact same calculation is:

!determine pseudorank:
do j=1,ldiag
    if (abs(a(j,j))<=tau) exit
end do
k=j-1
kp1=j

As you can see, no line numbers or GOTO statements are required. The new version even eliminates one assignment and one addition operation. Note that the refactored version depends on the fact that the index of the DO loop, if it completes the loop (i.e., if the exit statement is not triggered), will have a value of ldiag+1. This behavior has been part of the Fortran standard for some time (perhaps it was not when this routine was written?).

There is also a C translation of SLSQP available, which fixes some of the issues in the original code. Their version of the above code snippet is a pretty straightforward translation of the FORTRAN 77 version, except with all the ugliness of C on full display (a[j + j * a_dim1], seriously?):

/* DETERMINE PSEUDORANK */
i__2 = ldiag;
for (j = 1; j <= i__2; ++j) {
    /* L90: */
    if ((d__1 = a[j + j * a_dim1], fabs(d__1)) <= *tau) {
        goto L100;
    }
}
k = ldiag;
goto L110;
L100:
k = j - 1;
L110:
kp1 = k + 1;

See Also

1. Dieter Kraft, "A Software Package for Sequential Quadratic Programming", DFVLR-FB 88-28, 1988.
2. Dieter Kraft, "Algorithm 733: TOMP–Fortran Modules for Optimal Control Calculations," ACM Transactions on Mathematical Software, Vol. 20, No. 3, p. 262-281 (1994).
3. John Burkardt, LAWSON Least Squares Routines, 21 October 2008. [Fortran 90 versions of the least squares routines used in SLSQP].

Pikaia

I've started a new project on Github for a new modern object-oriented version of the Pikaia genetic algorithm code. This is a refactoring and upgrade of the Pikaia code from the High Altitude Observatory. The original code is public domain and was written by Paul Charbonneau & Barry Knapp (version 1.2 was released in 2003). The new code differs from the old code in the following respects:

• The original fixed-form source (FORTRAN 77) was converted to free-form source.
• The code is now object-oriented Fortran 2003/2008. All user interaction is now through a class, which is the only public entity in the module.
• All real variables are now 8 bytes (a.k.a. "double precision"). The precision can also be changed by the user by modifying the wp parameter.
• The random number generator was replaced with calls to the intrinsic Fortran random_number function.
• There are various new options (e.g., a convergence window with a tolerance can be specified as a stopping condition, and the user can specify a subroutine for reporting the best solution at each generation).
• Mapping the variables to be between 0 and 1 now occurs internally, rather than requiring the user to do it.
• Can now include an initial guess in the initial population.

This is another example of how older Fortran codes can be refactored to bring them up to date with modern computing concepts without doing that much work. In my opinion, the object-oriented Fortran 2003 interface is a lot better than the old FORTRAN 77 version. For one, it's easier to follow. Also, data can now easily be passed into the user fitness function by extending the pikaia class and putting the data there. No common blocks necessary!

References

1. Original Pikaia code and documentation [High Altitude Observatory]

Multidimensional B-Spline Interpolation

I just started a new modern Fortran software library called bspline-fortran, which is for multidimensional (multivariate) b-spline interpolation of data defined on a regular grid. It is available on GitHub, and released under a permissive BSD-style license.

It seems impossible to find code for higher than 3D spline interpolation on the internet. Einspline only has 1D-3D, as do the NIST Core Math Library DBSPLIN and DTENSBS routines. Python's SciPy stops at 2D (Bivariate splines). At first glance, the SciPy routine map_coordinates seems to do what I want, but not really since there doesn't seem to be any way to specify the abscissa vectors (x, y, z, etc.). Note: maybe there is a way, but looking at the less-than-great documentation, the minimally-commented C code, and then reading several confusing Stack Overflow posts didn't help me much. Apparently, I'm not the only one confused by this routine.

After much searching, I finally just took the 2D and 3D NIST routines (written in 1982), refactored them significantly so I could better understand what they were doing, and then extended the algorithm into higher dimensions (which is actually quite easy to do for b-splines). The original FORTRAN 77 code was somewhat hard to follow, since it was stuffing matrices into a giant WORK vector, which required a lot of obscure bookkeeping of indices. For example, I replaced this bit of code:

    IZM1 = IZ - 1  
    KCOLY = LEFTY - KY + 1  
    DO 60 K=1,KZ  
      I = (K-1)*KY + 1  
      J = IZM1 + K  
      WORK(J) = DBVALU(TY(KCOLY),WORK(I),KY,KY,IDY,YVAL,INBV1,WORK(IW))  
60  CONTINUE  

with this:

kcoly = lefty - ky + 1  
do k=1,kz  
    temp2(k) = dbvalu(ty(kcoly:),temp1(:,k),ky,ky,idy,yval,inbv1,work)  
end do  

which makes it a lot easier to deal with and add the extra dimensions as necessary.

The new library contains routines for 2D, 3D, 4D, 5D, and 6D interpolation. It seems like someone else may find them useful, I don't know why they don't seem to be available anywhere else. Eventually, I'll add object-oriented wrappers for the core routines, to make them easier to use.

Fixed to Free Form Fortran Conversion

Old style fixed-form Fortran code (commonly called FORTRAN 77 style) was replaced by free-form style in 1991 with the introduction of the Fortran 90 standard. In spite of this, fixed-form code can still be found in legacy projects, and there are some people who still write it for whatever reason (possibly unaware that a better format exists). There are also a large number of high-quality legacy fixed-form code libraries from back in the day that still work great. All modern Fortran compilers accept both fixed and free-form code, but there is very little reason for new fixed-form code to be written today. Also, it is often convenient to convert old-style code to free-format if it is going to be maintained or upgraded by a programmer in the present day. The following list provides links to several free tools to convert fixed-form code to free-form code (there are also several commercially-available solutions):

• convert (Michael Metcalf)
• to_f90 (Alan Miller)
• f2f (Colby Lemon)
• Camfort (Dominic Orchard)

See also

1. Source Form Just Wants to be Free
2. Modernizing Old Fortran