Topological Sorting
Topological sorting can be used to determine the order in which a collection of interdependent tasks must be performed. For example, when building a complex modern Fortran application, there can be many modules with complex interdependencies (via use association). A Fortran building system (like FoBiS, Foray, or SCons) will perform a topological sort to determine the correct compilation order. In graph theory, the collection of tasks are vertices of a directed graph. If there are no circular dependencies, then it is a directed acyclic graph (DAG).
An example modern Fortran implementation of a topological sorting algorithm is given here. The only public class is dag, which is used to define the graph and perform the sort. The toposort method performs a "depth-first" traversal of the graph using the recursive subroutine dfs. Each vertex is only visited once, and so the algorithm runs in linear time. The routine also triggers an error message for circular dependencies.
module toposort_module
!! Topological sorting, using a recursive
!! depth-first method. The vertices are
!! integer values from (1, 2, ..., nvertices)
implicit none
private
type :: vertex
!! a vertex of a directed acyclic graph (DAG)
integer,dimension(:),allocatable :: edges
integer :: ivertex = 0 !vertex number
logical :: checking = .false.
logical :: marked = .false.
contains
procedure :: set_edges
end type vertex
type,public :: dag
!! a directed acyclic graph (DAG)
type(vertex),dimension(:),allocatable :: vertices
contains
procedure :: set_vertices => dag_set_vertices
procedure :: set_edges => dag_set_edges
procedure :: toposort => dag_toposort
end type dag
contains
subroutine set_edges(me,edges)
!! specify the edge indices for this vertex
implicit none
class(vertex),intent(inout) :: me
integer,dimension(:),intent(in) :: edges
allocate(me%edges(size(edges)))
me%edges = edges
end subroutine set_edges
subroutine dag_set_vertices(me,nvertices)
!! set the number of vertices in the dag
implicit none
class(dag),intent(inout) :: me
integer,intent(in) :: nvertices !! number of vertices
integer :: i
allocate(me%vertices(nvertices))
me%vertices%ivertex = [(i,i=1,nvertices)]
end subroutine dag_set_vertices
subroutine dag_set_edges(me,ivertex,edges)
!! set the edges for a vertex in a dag
implicit none
class(dag),intent(inout) :: me
integer,intent(in) :: ivertex !! vertex number
integer,dimension(:),intent(in) :: edges
call me%vertices(ivertex)%set_edges(edges)
end subroutine dag_set_edges
subroutine dag_toposort(me,order)
!! main toposort routine
implicit none
class(dag),intent(inout) :: me
integer,dimension(:),allocatable,intent(out) :: order
integer :: i,n,iorder
n = size(me%vertices)
allocate(order(n))
iorder = 0 ! index in order array
do i=1,n
if (.not. me%vertices(i)%marked) &
call dfs(me%vertices(i))
end do
contains
recursive subroutine dfs(v)
!! depth-first graph traversal
type(vertex),intent(inout) :: v
integer :: j
if (v%checking) then
error stop 'Error: circular dependency.'
else
if (.not. v%marked) then
v%checking = .true.
if (allocated(v%edges)) then
do j=1,size(v%edges)
call dfs(me%vertices(v%edges(j)))
end do
end if
v%checking = .false.
v%marked = .true.
iorder = iorder + 1
order(iorder) = v%ivertex
end if
end if
end subroutine dfs
end subroutine dag_toposort
end module toposort_module
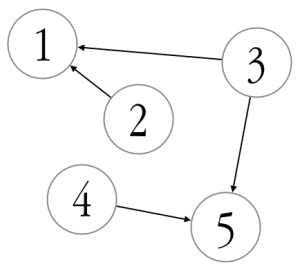
An example use of this module is given below. Here, we define a graph with five vertices: task 2 depends on 1, task 3 depends on both 1 and 5, and task 4 depends on 5.
program main
use toposort_module
implicit none
type(dag) :: d
integer,dimension(:),allocatable :: order
call d%set_vertices(5)
call d%set_edges(2,[1]) ! 2 depends on 1
call d%set_edges(3,[5,1]) ! 3 depends on 5 and 1
call d%set_edges(4,[5]) ! 4 depends on 5
call d%toposort(order)
write(*,*) order
end program main
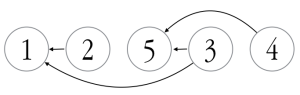
The result is:
Which is the evaluation order. As far as I can find, the above code is the only modern Fortran topological sorting implementation available on the internet. There is a FORTRAN 77 subroutine here, and a Fortran 90-ish one here (however, neither of them check for circular dependencies).
See also
- Topological Sorting [Everything Under The Sun], June 26, 2013.
- Topological sorting [Wikipedia]
- tsort -- UNIX command for performing topological sorting. [Note that this gives the result in the reverse order from the code listed above.]