Direct and Inverse

There are two standard problems in geodesy:
- Direct geodetic problem -- Given a point on the Earth (latitude and longitude) and the direction (azimuth) and distance from that point to a second point, determine the latitude and longitude of that second point.
- Inverse geodetic problem -- Given two points on the Earth, determine the azimuth and distance between them.
Assuming the Earth is an oblate spheroid, both of these can be solved using the iterative algorithms by Thaddeus Vincenty [1]. Modern Fortran versions of Vincenty's algorithms can be found in the geodesy module of the Fortran Astrodynamics Toolkit [2].
The direct algorithm was listed in an earlier post. If we assume a WGS84 Earth ellipsoid (a=6378.137 km, f=1/298.257223563), an example direct calculation is:
$$
\begin{array}{rcll}
\phi_1 &= & 29.97^{\circ} & \mathrm{(Latitude ~of ~ first ~ point)}\\
\lambda_1 &= & -95.35^{\circ} & \mathrm{(Longitude ~of ~ first ~point)} \\
Az &= & 20^{\circ} & \mathrm{(Azimuth)}\\
s &= & 50~\mathrm{km} & \mathrm{(Distance)}
\end{array}
$$
The latitude and longitude of the second point is:
$$
\begin{array}{rcl}
\phi_2 &= & 30.393716^{\circ} \\
\lambda_2 &= & -95.172057^{\circ} \\
\end{array}
$$
The more complicated inverse algorithm is listed here (based on the USNGS code from [1]):
subroutine inverse(a, rf, b1, l1, b2, l2, faz, baz, s, it, sig, lam, kind)
use, intrinsic :: iso_fortran_env, wp => real64
implicit none
real(wp), intent(in) :: a !! Equatorial semimajor axis
real(wp), intent(in) :: rf !! reciprocal flattening (1/f)
real(wp), intent(in) :: b1 !! latitude of point 1 (rad, positive north)
real(wp), intent(in) :: l1 !! longitude of point 1 (rad, positive east)
real(wp), intent(in) :: b2 !! latitude of point 2 (rad, positive north)
real(wp), intent(in) :: l2 !! longitude of point 2 (rad, positive east)
real(wp), intent(out) :: faz !! Forward azimuth (rad, clockwise from north)
real(wp), intent(out) :: baz !! Back azimuth (rad, clockwise from north)
real(wp), intent(out) :: s !! Ellipsoidal distance
integer, intent(out) :: it !! iteration count
real(wp), intent(out) :: sig !! spherical distance on auxiliary sphere
real(wp), intent(out) :: lam !! longitude difference on auxiliary sphere
integer, intent(out) :: kind !! solution flag: kind=1, long-line; kind=2, antipodal
real(wp) :: beta1, beta2, biga, bigb, bige, bigf, boa, &
c, cosal2, coslam, cossig, costm, costm2, &
cosu1, cosu2, d, dsig, ep2, l, prev, sinal, &
sinlam, sinsig, sinu1, sinu2, tem1, tem2, &
temp, test, z
real(wp), parameter :: pi = acos(-1.0_wp)
real(wp), parameter :: two_pi = 2.0_wp*pi
real(wp), parameter :: tol = 1.0e-14_wp !! convergence tolerance
real(wp), parameter :: eps = 1.0e-15_wp !! tolerance for zero
boa = 1.0_wp - 1.0_wp/rf
beta1 = atan(boa*tan(b1))
sinu1 = sin(beta1)
cosu1 = cos(beta1)
beta2 = atan(boa*tan(b2))
sinu2 = sin(beta2)
cosu2 = cos(beta2)
l = l2 - l1
if (l > pi) l = l - two_pi
if (l < -pi) l = l + two_pi
prev = l
test = l
it = 0
kind = 1
lam = l
longline: do ! long-line loop (kind=1)
sinlam = sin(lam)
coslam = cos(lam)
temp = cosu1*sinu2 - sinu1*cosu2*coslam
sinsig = sqrt((cosu2*sinlam)**2 + temp**2)
cossig = sinu1*sinu2 + cosu1*cosu2*coslam
sig = atan2(sinsig, cossig)
if (abs(sinsig) < eps) then
sinal = cosu1*cosu2*sinlam/sign(eps, sinsig)
else
sinal = cosu1*cosu2*sinlam/sinsig
end if
cosal2 = -sinal**2 + 1.0_wp
if (abs(cosal2) < eps) then
costm = -2.0_wp*(sinu1*sinu2/sign(eps, &
cosal2)) + cossig
else
costm = -2.0_wp*(sinu1*sinu2/cosal2) + &
cossig
end if
costm2 = costm*costm
c = ((-3.0_wp*cosal2 + 4.0_wp)/rf + 4.0_wp)* &
cosal2/rf/16.0_wp
antipodal: do ! antipodal loop (kind=2)
it = it + 1
d = (((2.0_wp*costm2 - 1.0_wp)*cossig*c + &
costm)*sinsig*c + sig)*(1.0_wp - c)/rf
if (kind == 1) then
lam = l + d*sinal
if (abs(lam - test) >= tol) then
if (abs(lam) > pi) then
kind = 2
lam = pi
if (l < 0.0_wp) lam = -lam
sinal = 0.0_wp
cosal2 = 1.0_wp
test = 2.0_wp
prev = test
sig = pi - abs(atan(sinu1/cosu1) + &
atan(sinu2/cosu2))
sinsig = sin(sig)
cossig = cos(sig)
c = ((-3.0_wp*cosal2 + 4.0_wp)/rf + &
4.0_wp)*cosal2/rf/16.0_wp
if (abs(sinal - prev) < tol) exit longline
if (abs(cosal2) < eps) then
costm = -2.0_wp*(sinu1*sinu2/ &
sign(eps, cosal2)) + cossig
else
costm = -2.0_wp*(sinu1*sinu2/cosal2) + &
cossig
end if
costm2 = costm*costm
cycle antipodal
end if
if (((lam - test)*(test - prev)) < 0.0_wp .and. it > 5) &
lam = (2.0_wp*lam + 3.0_wp*test + prev)/6.0_wp
prev = test
test = lam
cycle longline
end if
else
sinal = (lam - l)/d
if (((sinal - test)*(test - prev)) < 0.0_wp .and. it > 5) &
sinal = (2.0_wp*sinal + 3.0_wp*test + prev)/6.0_wp
prev = test
test = sinal
cosal2 = -sinal**2 + 1.0_wp
sinlam = sinal*sinsig/(cosu1*cosu2)
coslam = -sqrt(abs(-sinlam**2 + 1.0_wp))
lam = atan2(sinlam, coslam)
temp = cosu1*sinu2 - sinu1*cosu2*coslam
sinsig = sqrt((cosu2*sinlam)**2 + temp**2)
cossig = sinu1*sinu2 + cosu1*cosu2*coslam
sig = atan2(sinsig, cossig)
c = ((-3.0_wp*cosal2 + 4.0_wp)/rf + 4.0_wp)* &
cosal2/rf/16.0_wp
if (abs(sinal - prev) >= tol) then
if (abs(cosal2) < eps) then
costm = -2.0_wp*(sinu1*sinu2/ &
sign(eps, cosal2)) + cossig
else
costm = -2.0_wp*(sinu1*sinu2/cosal2) + &
cossig
end if
costm2 = costm*costm
cycle antipodal
end if
end if
exit longline
end do antipodal
end do longline
if (kind == 2) then ! antipodal
faz = sinal/cosu1
baz = sqrt(-faz**2 + 1.0_wp)
if (temp < 0.0_wp) baz = -baz
faz = atan2(faz, baz)
tem1 = -sinal
tem2 = sinu1*sinsig - cosu1*cossig*baz
baz = atan2(tem1, tem2)
else ! long-line
tem1 = cosu2*sinlam
tem2 = cosu1*sinu2 - sinu1*cosu2*coslam
faz = atan2(tem1, tem2)
tem1 = -cosu1*sinlam
tem2 = sinu1*cosu2 - cosu1*sinu2*coslam
baz = atan2(tem1, tem2)
end if
if (faz < 0.0_wp) faz = faz + two_pi
if (baz < 0.0_wp) baz = baz + two_pi
ep2 = 1.0_wp/(boa*boa) - 1.0_wp
bige = sqrt(1.0_wp + ep2*cosal2)
bigf = (bige - 1.0_wp)/(bige + 1.0_wp)
biga = (1.0_wp + bigf*bigf/4.0_wp)/(1.0_wp - bigf)
bigb = bigf*(1.0_wp - 0.375_wp*bigf*bigf)
z = bigb/6.0_wp*costm*(-3.0_wp + 4.0_wp* &
sinsig**2)*(-3.0_wp + 4.0_wp*costm2)
dsig = bigb*sinsig*(costm + bigb/4.0_wp* &
(cossig*(-1.0_wp + 2.0_wp*costm2) - z))
s = (boa*a)*biga*(sig - dsig)
end subroutine inverse
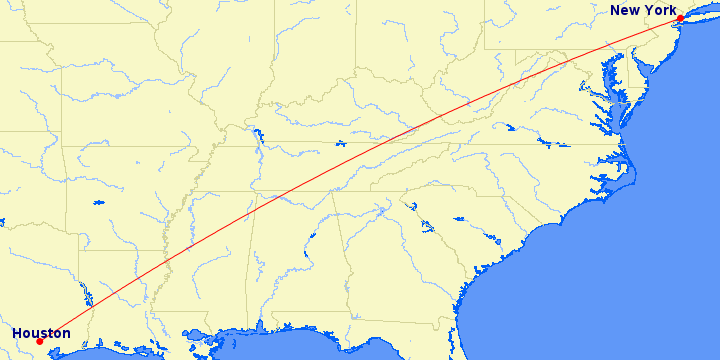
For the same ellipsoid, an example inverse calculation is:
$$
\begin{array}{rcll}
\phi_1 &= & 29.97^{\circ} & \mathrm{(Latitude ~of ~ first ~ point)}\\
\lambda_1 &= & -95.35^{\circ} & \mathrm{(Longitude ~of ~ first ~point)} \\
\phi_2 &= & 40.77^{\circ} & \mathrm{(Latitude ~of ~ second ~ point)}\\
\lambda_2 &= & -73.98^{\circ} & \mathrm{(Longitude ~of ~ second ~point)}
\end{array}
$$
The azimuth and distance from the first to the second point is:
$$
\begin{array}{rcl}
Az &= & 52.400056^{\circ} & \mathrm{(Azimuth)}\\
s &= & 2272.497~\mathrm{km} & \mathrm{(Distance)}
\end{array}
$$
References
- T. Vincenty, "Direct and Inverse Solutions of Geodesics on the Ellipsoid with Application of Nested Equations". Survey Review XXII. 176, April 1975. [sourcecode from the U.S. National Geodetic Survey].
- geodesy_module from the Fortran Astrodynamics Toolkit.