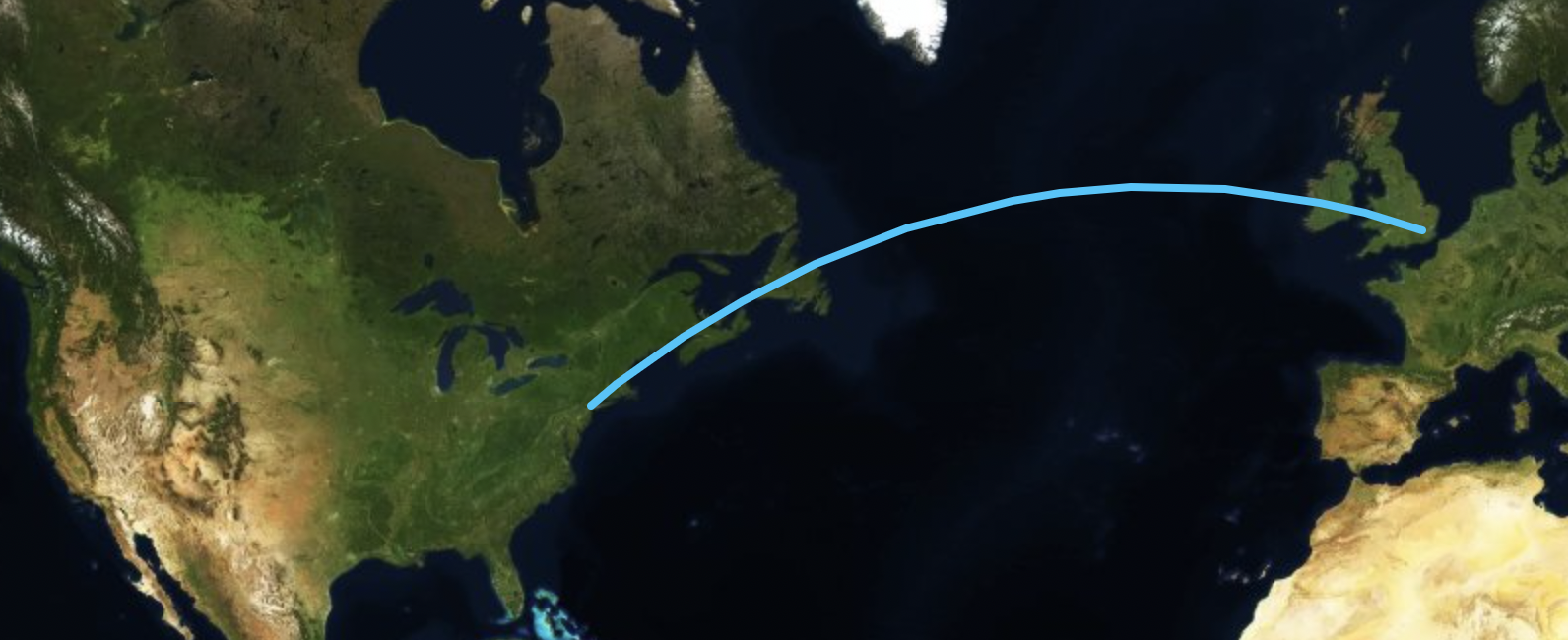
If we assume that the Earth is a sphere of radius \(r\), the shortest distance between two sites (\([\phi_1,\lambda_1]\) and \([\phi_2,\lambda_2]\)) on the surface is the great-circle distance, which can be computed in several ways:
Law of Cosines equation:
$$
d = r \arccos\bigl(\sin\phi_1\cdot\sin\phi_2+\cos\phi_1\cdot\cos\phi_2\cdot\cos(\Delta\lambda)\bigr)
$$
This equation, while mathematically correct, is not usually recommended for use, since it is ill-conditioned for sites that are very close to each other.
Using the haversine equation:
$$
d = 2 r \arcsin \sqrt{\sin^2\left(\frac{\Delta\phi}{2}\right)+\cos{\phi_1}\cdot\cos{\phi_2}\cdot\sin^2\left(\frac{\Delta\lambda}{2}\right)}
$$
The haversine one is better, but can be ill-conditioned for near antipodal points.
Using the Vincenty equation:
$$
d = r \arctan \frac{\sqrt{\left(\cos\phi_2\cdot\sin(\Delta\lambda)\right)^2+\left(\cos\phi_1\cdot\sin\phi_2-\sin\phi_1\cdot\cos\phi_2\cdot\cos(\Delta\lambda)\right)^2}}{\sin\phi_1\cdot\sin\phi_2+\cos\phi_1\cdot\cos\phi_2\cdot\cos(\Delta\lambda)}
$$
This one is accurate for any two points on a sphere.
Code
Fortran implementations of these algorithms are given here:
Law of Cosines:
pure function gcdist(r,lat1,long1,lat2,long2) &
result(d)
implicit none
real(wp) :: d !! great circle distance from 1 to 2 [km]
real(wp),intent(in) :: r !! radius of the body [km]
real(wp),intent(in) :: long1 !! longitude of first site [rad]
real(wp),intent(in) :: lat1 !! latitude of the first site [rad]
real(wp),intent(in) :: long2 !! longitude of the second site [rad]
real(wp),intent(in) :: lat2 !! latitude of the second site [rad]
real(wp) :: clat1,clat2,slat1,slat2,dlon,cdlon
clat1 = cos(lat1)
clat2 = cos(lat2)
slat1 = sin(lat1)
slat2 = sin(lat2)
dlon = long1-long2
cdlon = cos(dlon)
d = r * acos(slat1*slat2+clat1*clat2*cdlon)
end function gcdist
Haversine:
pure function gcdist_haversine(r,lat1,long1,lat2,long2) &
result(d)
implicit none
real(wp) :: d !! great circle distance from 1 to 2 [km]
real(wp),intent(in) :: r !! radius of the body [km]
real(wp),intent(in) :: long1 !! longitude of first site [rad]
real(wp),intent(in) :: lat1 !! latitude of the first site [rad]
real(wp),intent(in) :: long2 !! longitude of the second site [rad]
real(wp),intent(in) :: lat2 !! latitude of the second site [rad]
real(wp) :: dlat,clat1,clat2,dlon,a
dlat = lat1-lat2
clat1 = cos(lat1)
clat2 = cos(lat2)
dlon = long1-long2
a = sin(dlat/2.0_wp)**2 + clat1*clat2*sin(dlon/2.0_wp)**2
d = r * 2.0_wp * asin(min(1.0_wp,sqrt(a)))
end function gcdist_haversine
Vincenty:
pure function gcdist_vincenty(r,lat1,long1,lat2,long2) &
result(d)
implicit none
real(wp) :: d !! great circle distance from 1 to 2 [km]
real(wp),intent(in) :: r !! radius of the body [km]
real(wp),intent(in) :: long1 !! longitude of first site [rad]
real(wp),intent(in) :: lat1 !! latitude of the first site [rad]
real(wp),intent(in) :: long2 !! longitude of the second site [rad]
real(wp),intent(in) :: lat2 !! latitude of the second site [rad]
real(wp) :: c1,s1,c2,s2,dlon,clon,slon
c1 = cos(lat1)
s1 = sin(lat1)
c2 = cos(lat2)
s2 = sin(lat2)
dlon = long1-long2
clon = cos(dlon)
slon = sin(dlon)
d = r*atan2(sqrt((c2*slon)**2+(c1*s2-s1*c2*clon)**2), &
(s1*s2+c1*c2*clon))
end function gcdist_vincenty
Test cases
Using a radius of the Earth of 6,378,137 meters, here are a few test cases (using double precision (real64) arithmetic):
Close points
The distance between the following very close points \(([\phi_1,\lambda_1], [\phi_2,\lambda_2]) =([0, 0.000001], [0.0, 0.0])\) (radians) is:
| Algorithm |
Procedure |
Result (meters) |
| Law of Cosines |
gcdist |
6.3784205037462689 |
| Haversine |
gcdist_haversine |
6.3781369999999997 |
| Vincenty |
gcdist_vincenty |
6.3781369999999997 |
Houston to New York
The distance between the following two points \(([\phi_1,\lambda_1], [\phi_2,\lambda_2]) =([29.97, -95.35], [40.77, -73.98])\) (deg) is:
| Algorithm |
Procedure |
Result (meters) |
| Law of Cosines |
gcdist |
2272779.3057236285 |
| Haversine |
gcdist_haversine |
2272779.3057236294 |
| Vincenty |
gcdist_vincenty |
2272779.3057236290 |
Antipodal points
The distance between the following two antipodal points \(([\phi_1,\lambda_1], [\phi_2,\lambda_2]) = ([0, 0], [0.0, \pi/2])\) (radians) is:
| Algorithm |
Procedure |
Result (meters) |
| Law of Cosines |
gcdist |
20037508.342789244 |
| Haversine |
gcdist_haversine |
20037508.342789244 |
| Vincenty |
gcdist_vincenty |
20037508.342789244 |
Nearly antipodal points
The distance between the following two nearly antipodal points \(([\phi_1,\lambda_1], [\phi_2,\lambda_2]) = ([10^{-8}, 10^{-8}], [0.0, \pi/2])\) (radians) is:
| Algorithm |
Procedure |
Result (meters) |
| Law of Cosines |
gcdist |
20037508.342789244 |
| Haversine |
gcdist_haversine |
20037508.342789244 |
| Vincenty |
gcdist_vincenty |
20037508.252588764 |
Other methods
For a more accurate result, using an oblate-spheroid model of the Earth, the Vincenty inverse geodetic algorithm can be used (the equation above is just a special case of the more general algorithm when the ellipsoidal major and minor axes are equal). For the Houston to New York case, the difference between the spherical and oblate-spheroid equations is 282 meters.
See also

*Thaddeus Vincenty (1920--2002) Image source: [IAG Newsletter](http://www.gfy.ku.dk/~iag/newslett/news7606.htm)*
There are two standard problems in geodesy:
- Direct geodetic problem -- Given a point on the Earth (latitude and longitude) and the direction (azimuth) and distance from that point to a second point, determine the latitude and longitude of that second point.
- Inverse geodetic problem -- Given two points on the Earth, determine the azimuth and distance between them.
Assuming the Earth is an oblate spheroid, both of these can be solved using the iterative algorithms by Thaddeus Vincenty [1]. Modern Fortran versions of Vincenty's algorithms can be found in the geodesy module of the Fortran Astrodynamics Toolkit [2].
The direct algorithm was listed in an earlier post. If we assume a WGS84 Earth ellipsoid (a=6378.137 km, f=1/298.257223563), an example direct calculation is:
$$
\begin{array}{rcll}
\phi_1 &= & 29.97^{\circ} & \mathrm{(Latitude ~of ~ first ~ point)}\\
\lambda_1 &= & -95.35^{\circ} & \mathrm{(Longitude ~of ~ first ~point)} \\
Az &= & 20^{\circ} & \mathrm{(Azimuth)}\\
s &= & 50~\mathrm{km} & \mathrm{(Distance)}
\end{array}
$$
The latitude and longitude of the second point is:
$$
\begin{array}{rcl}
\phi_2 &= & 30.393716^{\circ} \\
\lambda_2 &= & -95.172057^{\circ} \\
\end{array}
$$
The more complicated inverse algorithm is listed here (based on the USNGS code from [1]):
subroutine inverse(a, rf, b1, l1, b2, l2, faz, baz, s, it, sig, lam, kind)
use, intrinsic :: iso_fortran_env, wp => real64
implicit none
real(wp), intent(in) :: a !! Equatorial semimajor axis
real(wp), intent(in) :: rf !! reciprocal flattening (1/f)
real(wp), intent(in) :: b1 !! latitude of point 1 (rad, positive north)
real(wp), intent(in) :: l1 !! longitude of point 1 (rad, positive east)
real(wp), intent(in) :: b2 !! latitude of point 2 (rad, positive north)
real(wp), intent(in) :: l2 !! longitude of point 2 (rad, positive east)
real(wp), intent(out) :: faz !! Forward azimuth (rad, clockwise from north)
real(wp), intent(out) :: baz !! Back azimuth (rad, clockwise from north)
real(wp), intent(out) :: s !! Ellipsoidal distance
integer, intent(out) :: it !! iteration count
real(wp), intent(out) :: sig !! spherical distance on auxiliary sphere
real(wp), intent(out) :: lam !! longitude difference on auxiliary sphere
integer, intent(out) :: kind !! solution flag: kind=1, long-line; kind=2, antipodal
real(wp) :: beta1, beta2, biga, bigb, bige, bigf, boa, &
c, cosal2, coslam, cossig, costm, costm2, &
cosu1, cosu2, d, dsig, ep2, l, prev, sinal, &
sinlam, sinsig, sinu1, sinu2, tem1, tem2, &
temp, test, z
real(wp), parameter :: pi = acos(-1.0_wp)
real(wp), parameter :: two_pi = 2.0_wp*pi
real(wp), parameter :: tol = 1.0e-14_wp !! convergence tolerance
real(wp), parameter :: eps = 1.0e-15_wp !! tolerance for zero
boa = 1.0_wp - 1.0_wp/rf
beta1 = atan(boa*tan(b1))
sinu1 = sin(beta1)
cosu1 = cos(beta1)
beta2 = atan(boa*tan(b2))
sinu2 = sin(beta2)
cosu2 = cos(beta2)
l = l2 - l1
if (l > pi) l = l - two_pi
if (l < -pi) l = l + two_pi
prev = l
test = l
it = 0
kind = 1
lam = l
longline: do ! long-line loop (kind=1)
sinlam = sin(lam)
coslam = cos(lam)
temp = cosu1*sinu2 - sinu1*cosu2*coslam
sinsig = sqrt((cosu2*sinlam)**2 + temp**2)
cossig = sinu1*sinu2 + cosu1*cosu2*coslam
sig = atan2(sinsig, cossig)
if (abs(sinsig) < eps) then
sinal = cosu1*cosu2*sinlam/sign(eps, sinsig)
else
sinal = cosu1*cosu2*sinlam/sinsig
end if
cosal2 = -sinal**2 + 1.0_wp
if (abs(cosal2) < eps) then
costm = -2.0_wp*(sinu1*sinu2/sign(eps, &
cosal2)) + cossig
else
costm = -2.0_wp*(sinu1*sinu2/cosal2) + &
cossig
end if
costm2 = costm*costm
c = ((-3.0_wp*cosal2 + 4.0_wp)/rf + 4.0_wp)* &
cosal2/rf/16.0_wp
antipodal: do ! antipodal loop (kind=2)
it = it + 1
d = (((2.0_wp*costm2 - 1.0_wp)*cossig*c + &
costm)*sinsig*c + sig)*(1.0_wp - c)/rf
if (kind == 1) then
lam = l + d*sinal
if (abs(lam - test) >= tol) then
if (abs(lam) > pi) then
kind = 2
lam = pi
if (l < 0.0_wp) lam = -lam
sinal = 0.0_wp
cosal2 = 1.0_wp
test = 2.0_wp
prev = test
sig = pi - abs(atan(sinu1/cosu1) + &
atan(sinu2/cosu2))
sinsig = sin(sig)
cossig = cos(sig)
c = ((-3.0_wp*cosal2 + 4.0_wp)/rf + &
4.0_wp)*cosal2/rf/16.0_wp
if (abs(sinal - prev) < tol) exit longline
if (abs(cosal2) < eps) then
costm = -2.0_wp*(sinu1*sinu2/ &
sign(eps, cosal2)) + cossig
else
costm = -2.0_wp*(sinu1*sinu2/cosal2) + &
cossig
end if
costm2 = costm*costm
cycle antipodal
end if
if (((lam - test)*(test - prev)) < 0.0_wp .and. it > 5) &
lam = (2.0_wp*lam + 3.0_wp*test + prev)/6.0_wp
prev = test
test = lam
cycle longline
end if
else
sinal = (lam - l)/d
if (((sinal - test)*(test - prev)) < 0.0_wp .and. it > 5) &
sinal = (2.0_wp*sinal + 3.0_wp*test + prev)/6.0_wp
prev = test
test = sinal
cosal2 = -sinal**2 + 1.0_wp
sinlam = sinal*sinsig/(cosu1*cosu2)
coslam = -sqrt(abs(-sinlam**2 + 1.0_wp))
lam = atan2(sinlam, coslam)
temp = cosu1*sinu2 - sinu1*cosu2*coslam
sinsig = sqrt((cosu2*sinlam)**2 + temp**2)
cossig = sinu1*sinu2 + cosu1*cosu2*coslam
sig = atan2(sinsig, cossig)
c = ((-3.0_wp*cosal2 + 4.0_wp)/rf + 4.0_wp)* &
cosal2/rf/16.0_wp
if (abs(sinal - prev) >= tol) then
if (abs(cosal2) < eps) then
costm = -2.0_wp*(sinu1*sinu2/ &
sign(eps, cosal2)) + cossig
else
costm = -2.0_wp*(sinu1*sinu2/cosal2) + &
cossig
end if
costm2 = costm*costm
cycle antipodal
end if
end if
exit longline
end do antipodal
end do longline
if (kind == 2) then ! antipodal
faz = sinal/cosu1
baz = sqrt(-faz**2 + 1.0_wp)
if (temp < 0.0_wp) baz = -baz
faz = atan2(faz, baz)
tem1 = -sinal
tem2 = sinu1*sinsig - cosu1*cossig*baz
baz = atan2(tem1, tem2)
else ! long-line
tem1 = cosu2*sinlam
tem2 = cosu1*sinu2 - sinu1*cosu2*coslam
faz = atan2(tem1, tem2)
tem1 = -cosu1*sinlam
tem2 = sinu1*cosu2 - cosu1*sinu2*coslam
baz = atan2(tem1, tem2)
end if
if (faz < 0.0_wp) faz = faz + two_pi
if (baz < 0.0_wp) baz = baz + two_pi
ep2 = 1.0_wp/(boa*boa) - 1.0_wp
bige = sqrt(1.0_wp + ep2*cosal2)
bigf = (bige - 1.0_wp)/(bige + 1.0_wp)
biga = (1.0_wp + bigf*bigf/4.0_wp)/(1.0_wp - bigf)
bigb = bigf*(1.0_wp - 0.375_wp*bigf*bigf)
z = bigb/6.0_wp*costm*(-3.0_wp + 4.0_wp* &
sinsig**2)*(-3.0_wp + 4.0_wp*costm2)
dsig = bigb*sinsig*(costm + bigb/4.0_wp* &
(cossig*(-1.0_wp + 2.0_wp*costm2) - z))
s = (boa*a)*biga*(sig - dsig)
end subroutine inverse
For the same ellipsoid, an example inverse calculation is:
$$
\begin{array}{rcll}
\phi_1 &= & 29.97^{\circ} & \mathrm{(Latitude ~of ~ first ~ point)}\\
\lambda_1 &= & -95.35^{\circ} & \mathrm{(Longitude ~of ~ first ~point)} \\
\phi_2 &= & 40.77^{\circ} & \mathrm{(Latitude ~of ~ second ~ point)}\\
\lambda_2 &= & -73.98^{\circ} & \mathrm{(Longitude ~of ~ second ~point)}
\end{array}
$$
The azimuth and distance from the first to the second point is:
$$
\begin{array}{rcl}
Az &= & 52.400056^{\circ} & \mathrm{(Azimuth)}\\
s &= & 2272.497~\mathrm{km} & \mathrm{(Distance)}
\end{array}
$$
References

The IAU Working Group on Cartographic Coordinates and Rotational Elements (WGCCRE) is the keeper of official models that describe the cartographic coordinates and rotational elements of planetary bodies (such as the Earth, satellites, minor planets, and comets). Periodically, they release a report containing the coefficients to compute body orientations, based on the latest data available. These coefficients allow one to compute the rotation matrix from the ICRF frame to a body-fixed frame (for example, IAU Earth) by giving the direction of the pole vector and the prime meridian location as functions of time. An example Fortran module illustrating this for the IAU Earth frame is given below. The coefficients are taken from the 2009 IAU report [Reference 1]. Note that the IAU models are also available in SPICE (as "IAU_EARTH", "IAU_MOON", etc.). For Earth, the IAU model is not suitable for use in applications that require the highest possible accuracy (for that a more complex model would be necessary), but is quite acceptable for many applications.
module iau_orientation_module
use, intrinsic :: iso_fortran_env, only: wp => real64
implicit none
private
!constants:
real(wp),parameter :: zero = 0.0_wp
real(wp),parameter :: one = 1.0_wp
real(wp),parameter :: pi = acos(-one)
real(wp),parameter :: pi2 = pi/2.0_wp
real(wp),parameter :: deg2rad = pi/180.0_wp
real(wp),parameter :: sec2day = one/86400.0_wp
real(wp),parameter :: sec2century = one/3155760000.0_wp
public :: icrf_to_iau_earth
contains
!Rotation matrix from ICRF to IAU_EARTH
pure function icrf_to_iau_earth(et) result(rotmat)
implicit none
real(wp),intent(in) :: et !ephemeris time [sec from J2000]
real(wp),dimension(3,3) :: rotmat !rotation matrix
real(wp) :: w,dec,ra,d,t
real(wp),dimension(3,3) :: tmp
d = et * sec2day !days from J2000
t = et * sec2century !Julian centuries from J2000
ra = ( - 0.641_wp * t ) * deg2rad
dec = ( 90.0_wp - 0.557_wp * t ) * deg2rad
w = ( 190.147_wp + 360.9856235_wp * d ) * deg2rad
!it is a 3-1-3 rotation:
tmp = matmul( rotmat_x(pi2-dec), rotmat_z(pi2+ra) )
rotmat = matmul( rotmat_z(w), tmp )
end function icrf_to_iau_earth
!The 3x3 rotation matrix for a rotation about the x-axis.
pure function rotmat_x(angle) result(rotmat)
implicit none
real(wp),dimension(3,3) :: rotmat !rotation matrix
real(wp),intent(in) :: angle !angle [rad]
real(wp) :: c,s
c = cos(angle)
s = sin(angle)
rotmat = reshape([one, zero, zero, &
zero, c, -s, &
zero, s, c],[3,3])
end function rotmat_x
!The 3x3 rotation matrix for a rotation about the z-axis.
pure function rotmat_z(angle) result(rotmat)
implicit none
real(wp),dimension(3,3) :: rotmat !rotation matrix
real(wp),intent(in) :: angle !angle [rad]
real(wp) :: c,s
c = cos(angle)
s = sin(angle)
rotmat = reshape([ c, -s, zero, &
s, c, zero, &
zero, zero, one ],[3,3])
end function rotmat_z
end module iau_orientation_module
References
- B. A. Archinal, et al., "Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2009", Celest Mech Dyn Astr (2011) 109:101-135.
- J. Williams, Fortran Astrodynamics Toolkit - iau_orientation_module [GitHub]
The gravitational potential of a non-homogeneous celestial body at radius \(r\), latitude \(\phi\) , and longitude \(\lambda\) can be represented in spherical coordinates as:
$$
U = \frac{\mu}{r} [ 1 + \sum\limits_{n=2}^{n_{max}} \sum\limits_{m=0}^{n} \left( \frac{r_e}{r} \right)^n P_{n,m}(\sin \phi) ( C_{n,m} \cos m\lambda + S_{n,m} \sin m\lambda ) ]
$$
Where \(r_e\) is the radius of the body, \(\mu\) is the gravitational parameter of the body, \(C_{n,m}\) and \(S_{n,m}\) are spherical harmonic coefficients, \(P_{n,m}\) are Associated Legendre Functions, and \(n_{max}\) is the desired degree and order of the approximation. The acceleration of a spacecraft at this location is the gradient of this potential. However, if the conventional representation of the potential given above is used, it will result in singularities at the poles \((\phi = \pm 90^{\circ})\), since the longitude becomes undefined at these points. (Also, evaluation on a computer would be relatively slow due to the number of sine and cosine terms).
A geopotential formulation that eliminates the polar singularity was devised by Samuel Pines in the early 1970s [1]. Over the years, various implementations and refinements of this algorithm and other similar algorithms have been published [2-7], mostly at the Johnson Space Center. The Fortran 77 code in Mueller [2] and Lear [4-5] is easily translated into modern Fortran. The Pines algorithm code from Spencer [3] appears to contain a few bugs, so translation is more of a challenge. A modern Fortran version (with bugs fixed) is presented below:
subroutine gravpot(r,nmax,re,mu,c,s,acc)
use, intrinsic :: iso_fortran_env, only: wp => real64
implicit none
real(wp),dimension(3),intent(in) :: r !position vector
integer,intent(in) :: nmax !degree/order
real(wp),intent(in) :: re !body radius
real(wp),intent(in) :: mu !grav constant
real(wp),dimension(nmax,0:nmax),intent(in) :: c !coefficients
real(wp),dimension(nmax,0:nmax),intent(in) :: s !
real(wp),dimension(3),intent(out) :: acc !grav acceleration
!local variables:
real(wp),dimension(nmax+1) :: creal, cimag, rho
real(wp),dimension(nmax+1,nmax+1) :: a,d,e,f
integer :: nax0,i,j,k,l,n,m
real(wp) :: rinv,ess,t,u,r0,rhozero,a1,a2,a3,a4,fac1,fac2,fac3,fac4
real(wp) :: ci1,si1
real(wp),parameter :: zero = 0.0_wp
real(wp),parameter :: one = 1.0_wp
!JW : not done in original paper,
! but seems to be necessary
! (probably assumed the compiler
! did it automatically)
a = zero
d = zero
e = zero
f = zero
!get the direction cosines ess, t and u:
nax0 = nmax + 1
rinv = one/norm2(r)
ess = r(1) * rinv
t = r(2) * rinv
u = r(3) * rinv
!generate the functions creal, cimag, a, d, e, f and rho:
r0 = re*rinv
rhozero = mu*rinv !JW: typo in original paper
rho(1) = r0*rhozero
creal(1) = ess
cimag(1) = t
d(1,1) = zero
e(1,1) = zero
f(1,1) = zero
a(1,1) = one
do i=2,nax0
if (i/=nax0) then !JW : to prevent access
ci1 = c(i,1) ! to c,s outside bounds
si1 = s(i,1)
else
ci1 = zero
si1 = zero
end if
rho(i) = r0*rho(i-1)
creal(i) = ess*creal(i-1) - t*cimag(i-1)
cimag(i) = ess*cimag(i-1) + t*creal(i-1)
d(i,1) = ess*ci1 + t*si1
e(i,1) = ci1
f(i,1) = si1
a(i,i) = (2*i-1)*a(i-1,i-1)
a(i,i-1) = u*a(i,i)
do k=2,i
if (i/=nax0) then
d(i,k) = c(i,k)*creal(k) + s(i,k)*cimag(k)
e(i,k) = c(i,k)*creal(k-1) + s(i,k)*cimag(k-1)
f(i,k) = s(i,k)*creal(k-1) - c(i,k)*cimag(k-1)
end if
!JW : typo here in original paper
! (should be GOTO 1, not GOTO 10)
if (i/=2) then
L = i-2
do j=1,L
a(i,i-j-1) = (u*a(i,i-j)-a(i-1,i-j))/(j+1)
end do
end if
end do
end do
!compute auxiliary quantities a1, a2, a3, a4
a1 = zero
a2 = zero
a3 = zero
a4 = rhozero*rinv
do n=2,nmax
fac1 = zero
fac2 = zero
fac3 = a(n,1) *c(n,0)
fac4 = a(n+1,1)*c(n,0)
do m=1,n
fac1 = fac1 + m*a(n,m) *e(n,m)
fac2 = fac2 + m*a(n,m) *f(n,m)
fac3 = fac3 + a(n,m+1) *d(n,m)
fac4 = fac4 + a(n+1,m+1)*d(n,m)
end do
a1 = a1 + rinv*rho(n)*fac1
a2 = a2 + rinv*rho(n)*fac2
a3 = a3 + rinv*rho(n)*fac3
a4 = a4 + rinv*rho(n)*fac4
end do
!gravitational acceleration vector:
acc(1) = a1 - ess*a4
acc(2) = a2 - t*a4
acc(3) = a3 - u*a4
end subroutine gravpot
References
- S. Pines. "Uniform Representation of the Gravitational Potential and its Derivatives", AIAA Journal, Vol. 11, No. 11, (1973), pp. 1508-1511.
- A. C. Mueller, "A Fast Recursive Algorithm for Calculating the Forces due to the Geopotential (Program: GEOPOT)", JSC Internal Note 75-FM-42, June 9, 1975.
- J. L. Spencer, "Pines Nonsingular Gravitational Potential Derivation, Description and Implementation", NASA Contractor Report 147478, February 9, 1976.
- W. M. Lear, "The Gravitational Acceleration Equations", JSC Internal Note 86-FM-15, April 1986.
- W. M. Lear, "The Programs TRAJ1 and TRAJ2", JSC Internal Note 87-FM-4, April 1987.
- R. G. Gottlieb, "Fast Gravity, Gravity Partials, Normalized Gravity, Gravity Gradient Torque and Magnetic Field: Derivation, Code and Data", NASA Contractor Report 188243, February, 1993.
- R. A. Eckman, A. J. Brown, and D. R. Adamo, "Normalization of Gravitational Acceleration Models", JSC-CN-23097, January 24, 2011.
The "direct" geodetic problem is: given the latitude and longitude of one point and the azimuth and distance to a second point, determine the latitude and longitude of that second point. The solution can be obtained using the algorithm by Polish American geodesist Thaddeus Vincenty [1]. A modern Fortran implementation is given below:
subroutine direct(a,f,glat1,glon1,glat2,glon2,faz,baz,s)
use, intrinsic :: iso_fortran_env, wp => real64
implicit none
real(wp),intent(in) :: a !semimajor axis of ellipsoid [m]
real(wp),intent(in) :: f !flattening of ellipsoid [-]
real(wp),intent(in) :: glat1 !latitude of 1 [rad]
real(wp),intent(in) :: glon1 !longitude of 1 [rad]
real(wp),intent(in) :: faz !forward azimuth 1->2 [rad]
real(wp),intent(in) :: s !distance from 1->2 [m]
real(wp),intent(out) :: glat2 !latitude of 2 [rad]
real(wp),intent(out) :: glon2 !longitude of 2 [rad]
real(wp),intent(out) :: baz !back azimuth 2->1 [rad]
real(wp) :: r,tu,sf,cf,cu,su,sa,csa,c2a,x,c,d,y,sy,cy,cz,e
real(wp),parameter :: pi = acos(-1.0_wp)
real(wp),parameter :: eps = 0.5e-13_wp
r = 1.0_wp-f
tu = r*sin(glat1)/cos(glat1)
sf = sin(faz)
cf = cos(faz)
baz = 0.0_wp
if (cf/=0.0_wp) baz = atan2(tu,cf)*2.0_wp
cu = 1.0_wp/sqrt(tu*tu+1.0_wp)
su = tu*cu
sa = cu*sf
c2a = -sa*sa+1.0_wp
x = sqrt((1.0_wp/r/r-1.0_wp)*c2a+1.0_wp)+1.0_wp
x = (x-2.0_wp)/x
c = 1.0_wp-x
c = (x*x/4.0_wp+1.0_wp)/c
d = (0.375_wp*x*x-1.0_wp)*x
tu = s/r/a/c
y = tu
do
sy = sin(y)
cy = cos(y)
cz = cos(baz+y)
e = cz*cz*2.0_wp-1.0_wp
c = y
x = e*cy
y = e+e-1.0_wp
y = (((sy*sy*4.0_wp-3.0_wp)*y*cz*d/6.0_wp+x)*d/4.0_wp-cz)*sy*d+tu
if (abs(y-c)<=eps) exit
end do
baz = cu*cy*cf-su*sy
c = r*sqrt(sa*sa+baz*baz)
d = su*cy+cu*sy*cf
glat2 = atan2(d,c)
c = cu*cy-su*sy*cf
x = atan2(sy*sf,c)
c = ((-3.0_wp*c2a+4.0_wp)*f+4.0_wp)*c2a*f/16.0_wp
d = ((e*cy*c+cz)*sy*c+y)*sa
glon2 = glon1+x-(1.0_wp-c)*d*f
baz = atan2(sa,baz)+pi
end subroutine direct
References
- T. Vincenty, "Direct and Inverse Solutions of Geodesics on the Ellipsoid with Application of Nested Equations", Survey Review XXII. 176, April 1975. [sourcecode from the U.S. National Geodetic Survey].
For many years, I have used the closed-form solution from Heikkinen [1] for converting Cartesian coordinates to geodetic latitude and altitude. I've never actually seen the original reference (which is in German). I coded up the algorithm from the table given in [2], and have used it ever since, in school and also at work. At one point I compared it with various other closed-form algorithms, and never found one that was faster and still had the same level of accuracy. However, I recently happened to stumble upon Olson's method [3], which seems to be better.
A Fortran implementation of Olson's algorithm is:
pure subroutine olson(rvec, a, b, h, lon, lat)
use, intrinsic :: iso_fortran_env, wp=>real64 !double precision
implicit none
real(wp),dimension(3),intent(in) :: rvec !position vector [km]
real(wp),intent(in) :: a ! geoid semimajor axis [km]
real(wp),intent(in) :: b ! geoid semiminor axis [km]
real(wp),intent(out) :: h ! geodetic altitude [km]
real(wp),intent(out) :: lon ! longitude [rad]
real(wp),intent(out) :: lat ! geodetic latitude [rad]
real(wp) :: f,x,y,z,e2,a1,a2,a3,a4,a5,a6,w,zp,&
w2,r2,r,s2,c2,u,v,s,ss,c,g,rg,rf,m,p,z2
x = rvec(1)
y = rvec(2)
z = rvec(3)
f = (a-b)/a
e2 = f * (2.0_wp - f)
a1 = a * e2
a2 = a1 * a1
a3 = a1 * e2 / 2.0_wp
a4 = 2.5_wp * a2
a5 = a1 + a3
a6 = 1.0_wp - e2
zp = abs(z)
w2 = x*x + y*y
w = sqrt(w2)
z2 = z * z
r2 = z2 + w2
r = sqrt(r2)
if (r < 100.0_wp) then
lat = 0.0_wp
lon = 0.0_wp
h = -1.0e7_wp
else
s2 = z2 / r2
c2 = w2 / r2
u = a2 / r
v = a3 - a4 / r
if (c2 > 0.3_wp) then
s = (zp / r) * (1.0_wp + c2 * (a1 + u + s2 * v) / r)
lat = asin(s)
ss = s * s
c = sqrt(1.0_wp - ss)
else
c = (w / r) * (1.0_wp - s2 * (a5 - u - c2 * v) / r)
lat = acos(c)
ss = 1.0_wp - c * c
s = sqrt(ss)
end if
g = 1.0_wp - e2 * ss
rg = a / sqrt(g)
rf = a6 * rg
u = w - rg * c
v = zp - rf * s
f = c * u + s * v
m = c * v - s * u
p = m / (rf / g + f)
lat = lat + p
if (z < 0.0_wp) lat = -lat
h = f + m * p / 2.0_wp
lon = atan2( y, x )
end if
end subroutine olson
For comparison, Heikkinen's algorithm is:
pure subroutine heikkinen(rvec, a, b, h, lon, lat)
use, intrinsic :: iso_fortran_env, wp=>real64 !double precision
implicit none
real(wp),dimension(3),intent(in) :: rvec !position vector [km]
real(wp),intent(in) :: a ! geoid semimajor axis [km]
real(wp),intent(in) :: b ! geoid semiminor axis [km]
real(wp),intent(out) :: h ! geodetic altitude [km]
real(wp),intent(out) :: lon ! longitude [rad]
real(wp),intent(out) :: lat ! geodetic latitude [rad]
real(wp) :: f,e_2,ep,r,e2,ff,g,c,s,pp,q,r0,u,v,z0,x,y,z,z2,r2,tmp,a2,b2
x = rvec(1)
y = rvec(2)
z = rvec(3)
a2 = a*a
b2 = b*b
f = (a-b)/a
e_2 = (2.0_wp*f-f*f)
ep = sqrt(a2/b2 - 1.0_wp)
z2 = z*z
r = sqrt(x**2 + y**2)
r2 = r*r
e2 = a2 - b2
ff = 54.0_wp * b2 * z2
g = r2 + (1.0_wp - e_2)*z2 - e_2*e2
c = e_2**2 * ff * r2 / g**3
s = (1.0_wp + c + sqrt(c**2 + 2.0_wp*c))**(1.0_wp/3.0_wp)
pp = ff / ( 3.0_wp*(s + 1.0_wp/s + 1.0_wp)**2 * g**2 )
q = sqrt( 1.0_wp + 2.0_wp*e_2**2 * pp )
r0 = -pp*e_2*r/(1.0_wp+q) + &
sqrt( max(0.0_wp, 1.0_wp/2.0_wp * a2 * (1.0_wp + 1.0_wp/q) - &
( pp*(1.0_wp-e_2)*z2 )/(q*(1.0_wp+q)) - &
1.0_wp/2.0_wp * pp * r2) )
u = sqrt( (r - e_2*r0)**2 + z2 )
v = sqrt( (r - e_2*r0)**2 + (1.0_wp - e_2)*z2 )
z0 = b**2 * z / (a*v)
h = u*(1.0_wp - b2/(a*v) )
lat = atan2( (z + ep**2*z0), r )
lon = atan2( y, x )
end subroutine heikkinen
Olson's is about 1.5 times faster on my 2.53 GHz i5 laptop, when both are compiled using gfortran with -O2 optimization (Olson: 3,743,212 cases/sec, Heikkinen: 2,499,670 cases/sec). The level of accuracy is about the same for each method.
References
- M. Heikkinen, "Geschlossene formeln zur berechnung raumlicher geodatischer koordinaten aus rechtwinkligen Koordinaten". Z. Ermess., 107 (1982), 207-211 (in German).
- E. D. Kaplan, "Understanding GPS: Principles and Applications", Artech House, 1996.
- D. K. Olson, "Converting Earth-Centered, Earth-Fixed Coordinates to Geodetic Coordinates," IEEE Transactions on Aerospace and Electronic Systems, 32 (1996) 473-476.




