Distant Retrograde Orbits

A "distant-retrograde orbit" (DRO) is a periodic orbit in the circular restricted three-body problem (CR3BP) that, in the rotating frame, looks like a large quasi-elliptical retrograde orbit around the secondary body. Moon-centered DRO's in the Earth-Moon system were considered as a possible destination for depositing a captured asteroid for NASA's proposed Asteroid Redirect Mission, since they can remain stable for long periods of time (decades or even centuries).
DROs can be computed using components from the Fortran Astrodynamics Toolkit. All we need is:
- A numerical integrator (we will use an 8th order Runge-Kutta method from Shanks [4]).
- The equations of motion for the circular restricted three-body problem (CR3BP).
- A nonlinear equation solver (we will use HYBRD1 from MINPACK).
We will use the canonical normalized CR3BP reference frame where the distance between the primary and secondary body is normalized to one. The initial state is placed on the x-axis, at a specified distance from the Moon. The y-velocity \(v_y\) is allowed to vary, and \(v_x=0\). The problem can be solved with two optimization variables:
- The time of flight for one orbit period (i.e., the duration between two consecutive x-axis crossings on the \(x>1\) side)
- The initial y-velocity component
and two constraints:
- \(y=0\) at the final time
- \(v_x=0\) at the final time (i.e., a perpendicular crossing of the x-axis)
The problem can be simplified to one variable and one constraint by using an integrator with an event-finding capability so that the integration proceeds until the x-axis crossing occurs (eliminating the time of flight and the \(y=0\) constraint from the optimization problem). That is how we will proceed here, since the Runge-Kutta module we are using does include an event location capability.
The code for computing a single Earth-Moon DRO is shown here:
program dro_test
use fortran_astrodynamics_toolkit
implicit none
real(wp), parameter :: mu_earth = 398600.436233_wp
!! km^3/s^2
real(wp), parameter :: mu_moon = 4902.800076_wp
!! km^3/s^2
integer, parameter :: n = 6
!! number of state variables
real(wp), parameter :: t0 = 0.0_wp
!! initial time (normalized)
real(wp), parameter :: tmax = 1000.0_wp
!! max final time (normalized)
real(wp), parameter :: dt = 0.001_wp
!! time step (normalized)
real(wp), parameter :: xtol = 1.0e-4_wp
!! tolerance for hybrd1
integer, parameter :: maxfev = 1000
!! max number of function evaluations for hybrd1
real(wp), dimension(n), parameter :: x0 = &
[1.2_wp, &
0.0_wp, &
0.0_wp, &
0.0_wp, &
-0.7_wp, &
0.0_wp]
!! initial guess for DRO state (normalized)
real(wp), dimension(1) :: vy0
!! initial y velocity (xvec for hybrd1)
real(wp), dimension(1) :: vxf
!! final x velocity (fvec for hybrd1)
real(wp) :: mu
!! CRTPB parameter
type(rk8_10_class) :: prop
!! integrator
integer :: info
!! hybrd1 status flag
! compute the CRTBP parameter & Jacobi constant:
mu = compute_crtpb_parameter(mu_earth, mu_moon)
! initialize integrator:
call prop%initialize(n, func, g=x_axis_crossing)
! now, solve for DRO:
vy0 = x0(5) ! initial guess
call hybrd1(dro_fcn, 1, vy0, vxf, tol=xtol, info=info)
! solution:
write (*, *) ' info=', info
write (*, *) ' vy0=', vy0
write (*, *) ' vxf=', vxf
contains
!**************************************
subroutine dro_fcn(n, xvec, fvec, iflag)
!! DRO function for hybrd1
implicit none
integer, intent(in) :: n !! `n=1` in this case
real(wp), dimension(n), intent(in) :: xvec !! `vy0`
real(wp), dimension(n), intent(out) :: fvec !! `vxf`
integer, intent(inout) :: iflag !! not used here
real(wp) :: gf, t0, tf_actual
real(wp), dimension(6) :: x, xf
real(wp), parameter :: tol = 1.0e-8_wp
!! event finding tolerance
t0 = zero ! epoch doesn't matter for crtbp
x = x0 ! initial guess state
x(5) = xvec(1) ! vy0 (only optimization variable)
!integrate to the next x-axis crossing:
call prop%integrate_to_event(t0, x, dt, tmax, tol, tf_actual, xf, gf)
!want x-velocity at the x-axis crossing to be zero:
fvec = xf(4)
end subroutine dro_fcn
!**************************************
subroutine func(me, t, x, xdot)
!! CRTBP derivative function
implicit none
class(rk_class), intent(inout) :: me
real(wp), intent(in) :: t
real(wp), dimension(me%n), intent(in) :: x
real(wp), dimension(me%n), intent(out) :: xdot
call crtbp_derivs(mu, x, xdot)
end subroutine func
!**************************************
subroutine x_axis_crossing(me, t, x, g)
!! x-axis crossing event function
implicit none
class(rk_class), intent(inout) :: me
real(wp), intent(in) :: t
real(wp), dimension(me%n), intent(in) :: x
real(wp), intent(out) :: g
g = x(2) ! y = 0 at x-axis crossing
end subroutine x_axis_crossing
end program dro_test
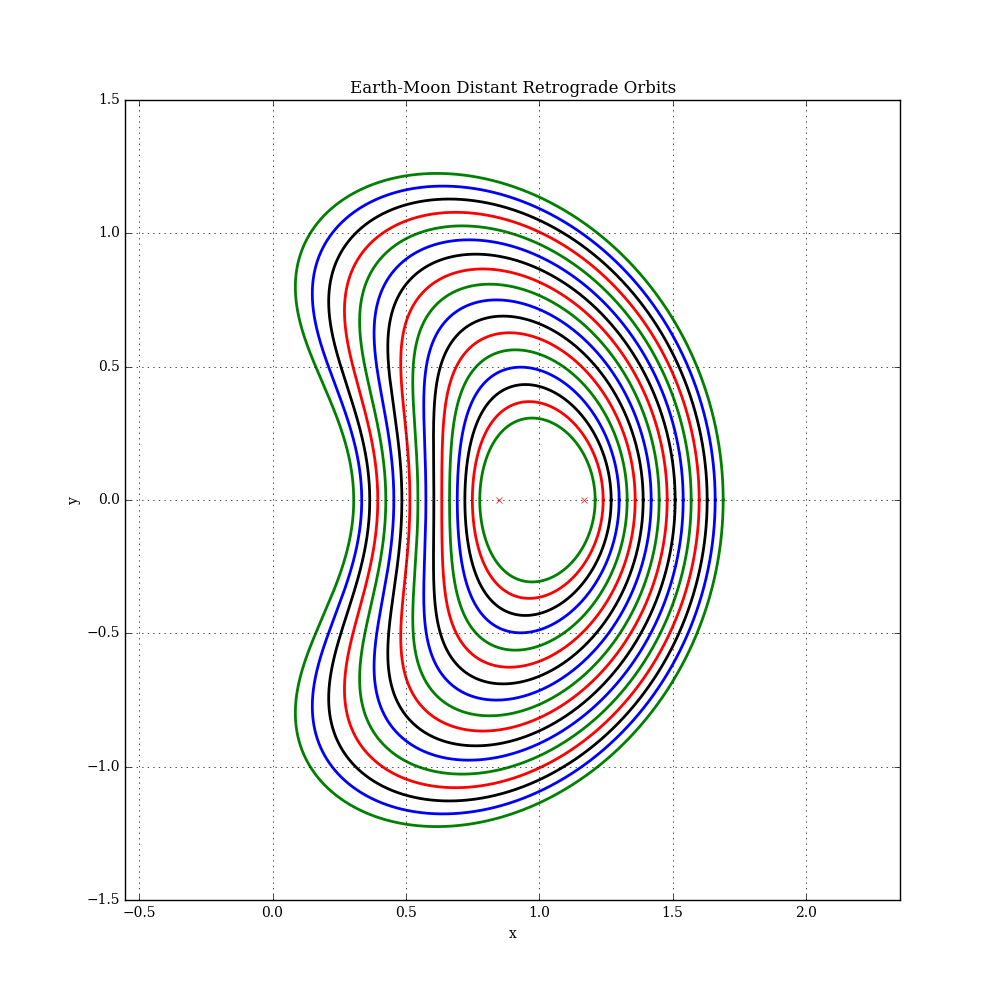
Trajectory plots for some example solutions are shown below (each with a different x component). The L1 and L2 libration points are also shown. In this plot, the Earth is at the origin and the Moon is at [x=1,y=0]. See this example for more details.
References
- The Restricted Three-Body Problem - MIT OpenCourseWare, S. Widnall 16.07 Dynamics Fall 2008, Version 1.0.
- C. A. Ocampo, G. W. Rosborough, "Transfer trajectories for distant retrograde orbiters of the Earth", AIAA Spaceflight Mechanics Meeting, Pasadena, CA, Feb. 22-24, 1993.
- Asteroid Redirect Mission and Human Space Flight, June 19, 2013.
- E. B. Shanks, "Higher Order Approximations of Runge-Kutta Type", NASA Technical Note, NASA TN D-2920, Sept. 1965.
- Henon, M., "Numerical Exploration of the Restricted Problem. V. Hill's Case: Periodic Orbits and Their Stability," Astronomy and Astrophys. Vol 1, 223-238, 1969.