Modified Equinoctial Elements
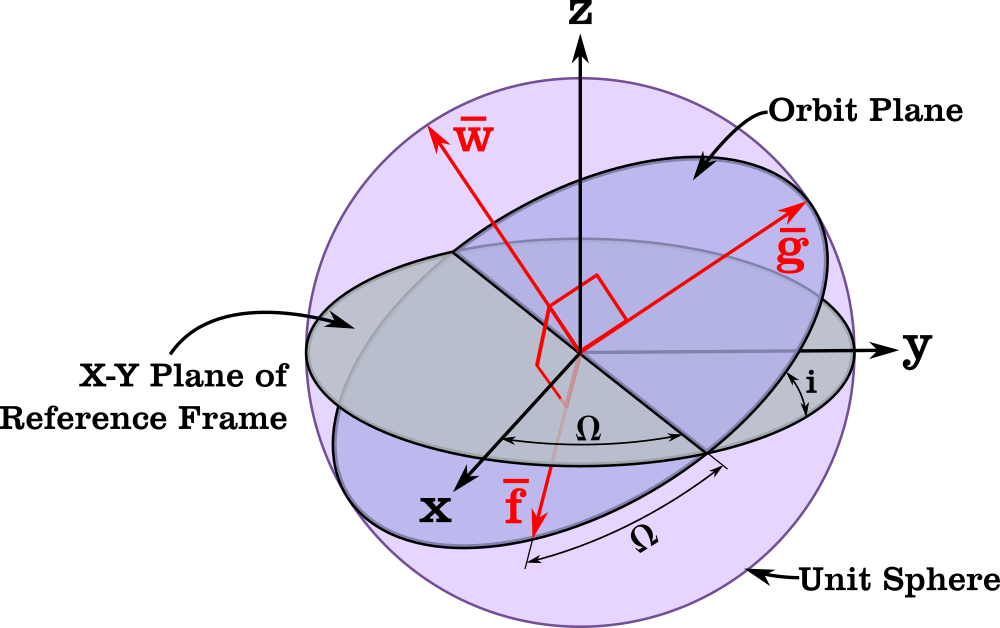
Last time, I mentioned an alternative orbital element set different from the classical elements. Modified equinoctial elements \((p,f,g,h,k,L)\) are another alternative that are applicable to all orbits and have nonsingular equations of motion (except for a singularity at \(i = \pi\)). They are defined as [1]:
- \(p = a (1 - e^2)\)
- \(f = e \cos (\omega + \Omega)\)
- \(g = e \sin (\omega + \Omega)\)
- \(h = \tan (i/2) \cos \Omega\)
- \(k = \tan (i/2) \sin \Omega\)
- \(L = \Omega + \omega + \nu\)
Where \(a\) is the semimajor axis, \(p\) is the semi-latus rectum, \(i\) is the inclination, \(e\) is the eccentricity, \(\omega\) is the argument of periapsis, \(\Omega\) is the right ascension of the ascending node, \(L\) is the true longitude, and \(\nu\) is the true anomaly. \((f,g)\) are the x and y components of the eccentricity vector in the orbital frame, and \((h,k)\) are the x and y components of the node vector in the orbital frame.
The conversion from Cartesian state (position and velocity) to modified equinoctial elements is given in this Fortran subroutine:
subroutine cartesian_to_equinoctial(mu,rv,evec)
use iso_fortran_env, only: wp => real64
implicit none
real(wp),intent(in) :: mu !! central body gravitational parameter (km^3/s^2)
real(wp),dimension(6),intent(in) :: rv !! Cartesian state vector
real(wp),dimension(6),intent(out) :: evec !! Modified equinoctial element vector: [p,f,g,h,k,L]
real(wp),dimension(3) :: r,v,hvec,hhat,ecc,fhat,ghat,rhat,vhat
real(wp) :: hmag,rmag,p,f,g,h,k,L,kk,hh,s2,tkh,rdv
r = rv(1:3)
v = rv(4:6)
rdv = dot_product(r,v)
rhat = unit(r)
rmag = norm2(r)
hvec = cross(r,v)
hmag = norm2(hvec)
hhat = unit(hvec)
vhat = (rmag*v - rdv*rhat)/hmag
p = hmag*hmag / mu
k = hhat(1)/(1.0_wp + hhat(3))
h = -hhat(2)/(1.0_wp + hhat(3))
kk = k*k
hh = h*h
s2 = 1.0_wp+hh+kk
tkh = 2.0_wp*k*h
ecc = cross(v,hvec)/mu - rhat
fhat(1) = 1.0_wp-kk+hh
fhat(2) = tkh
fhat(3) = -2.0_wp*k
ghat(1) = tkh
ghat(2) = 1.0_wp+kk-hh
ghat(3) = 2.0_wp*h
fhat = fhat/s2
ghat = ghat/s2
f = dot_product(ecc,fhat)
g = dot_product(ecc,ghat)
L = atan2(rhat(2)-vhat(1),rhat(1)+vhat(2))
evec = [p,f,g,h,k,L]
end subroutine cartesian_to_equinoctial
Where cross is a cross product function and unit is a unit vector function (\(\mathbf{u} = \mathbf{v} / |\mathbf{v}|\)).
The inverse routine (modified equinoctial to Cartesian) is:
subroutine equinoctial_to_cartesian(mu,evec,rv)
use iso_fortran_env, only: wp => real64
implicit none
real(wp),intent(in) :: mu !! central body gravitational parameter (km^3/s^2)
real(wp),dimension(6),intent(in) :: evec !! Modified equinoctial element vector : [p,f,g,h,k,L]
real(wp),dimension(6),intent(out) :: rv !! Cartesian state vector
real(wp) :: p,f,g,h,k,L,s2,r,w,cL,sL,smp,hh,kk,tkh
real(wp) :: x,y,xdot,ydot
real(wp),dimension(3) :: fhat,ghat
p = evec(1)
f = evec(2)
g = evec(3)
h = evec(4)
k = evec(5)
L = evec(6)
kk = k*k
hh = h*h
tkh = 2.0_wp*k*h
s2 = 1.0_wp + hh + kk
cL = cos(L)
sL = sin(L)
w = 1.0_wp + f*cL + g*sL
r = p/w
smp = sqrt(mu/p)
fhat(1) = 1.0_wp-kk+hh
fhat(2) = tkh
fhat(3) = -2.0_wp*k
ghat(1) = tkh
ghat(2) = 1.0_wp+kk-hh
ghat(3) = 2.0_wp*h
fhat = fhat/s2
ghat = ghat/s2
x = r*cL
y = r*sL
xdot = -smp * (g + sL)
ydot = smp * (f + cL)
rv(1:3) = x*fhat + y*ghat
rv(4:6) = xdot*fhat + ydot*ghat
end subroutine equinoctial_to_cartesian
The equations of motion are:
subroutine modified_equinoctial_derivs(mu,evec,scn,evecd)
use iso_fortran_env, only: wp => real64
implicit none
real(wp),intent(in) :: mu !! central body gravitational parameter (km^3/s^2)
real(wp),dimension(6),intent(in) :: evec !! modified equinoctial element vector : [p,f,g,h,k,L]
real(wp),dimension(3),intent(in) :: scn !! Perturbation (in the RSW frame) (km/sec^2)
real(wp),dimension(6),intent(out) :: evecd !! derivative of `evec`
real(wp) :: p,f,g,h,k,L,c,s,n,sqrtpm,sl,cl,s2no2w,s2,w
p = evec(1)
f = evec(2)
g = evec(3)
h = evec(4)
k = evec(5)
L = evec(6)
s = scn(1)
c = scn(2)
n = scn(3)
sqrtpm = sqrt(p/mu)
sl = sin(L)
cl = cos(L)
s2 = 1.0_wp + h*h + k*k
w = 1.0_wp + f*cl + g*sl
s2no2w = s2*n / (2.0_wp*w)
evecd(1) = (2.0_wp*p*c/w) * sqrtpm
evecd(2) = sqrtpm * ( s*sl + ((w+1.0_wp)*cl+f)*c/w - g*n*(h*sl-k*cl)/w )
evecd(3) = sqrtpm * (-s*cl + ((w+1.0_wp)*sl+g)*c/w + f*n*(h*sl-k*cl)/w )
evecd(4) = sqrtpm * s2no2w * cl
evecd(5) = sqrtpm * s2no2w * sl
evecd(6) = sqrt(mu*p)*(w/p)**2 + sqrtpm * ((h*sl-k*cl)*n)/w
end subroutine modified_equinoctial_derivs
The 3-element scn vector contains the components of the perturbing acceleration (e.g. from a thrusting engine, other celestial bodies, etc.) in the directions perpendicular to the radius vector, in the "along track" direction, and the direction of the angular momentum vector.
Integration using modified equinoctial elements will generally be more efficient than a Cowell type integration of the Cartesian state elements. You only have to worry about the one singularity (note that there is also an alternate retrograde formulation where the singularity is moved to \(i = 0\)).
See also
- Gooding Universal Elements [degenerateconic.com]
- modified_equinoctial_module in Fortran Astrodynamics Toolkit
References
- M. J. H. Walker, B. Ireland, Joyce Owens, "A Set of Modified Equinoctial Orbit Elements" Celestial Mechanics, Volume 36, Issue 4, p 409-419. (1985)
- Walker, M. J. H, "Erratum - a Set of Modified Equinoctial Orbit Elements" Celestial Mechanics, Volume 38, Issue 4, p 391-392. (1986)
- Broucke, R. A. & Cefola, P. J., "On the Equinoctial Orbit Elements" Celestial Mechanics, Volume 5, Issue 3, p 303-310. (1972)
- D. A. Danielson, C. P. Sagovac, B. Neta, L. W. Early, "Semianalytic Satellite Theory", Naval Postgraduate School Department of Mathematics, 1995
- P. J. Cefola, "Equinoctial orbit elements - Application to artificial satellite orbits", Astrodynamics Conference, 11-12 September 1972.