Numerical Differentiation

I present the initial release of a new modern Fortran library for computing Jacobian matrices using numerical differentiation. It is called NumDiff and is available on GitHub. The Jacobian is the matrix of partial derivatives of a set of \(m\) functions with respect to \(n\) variables:
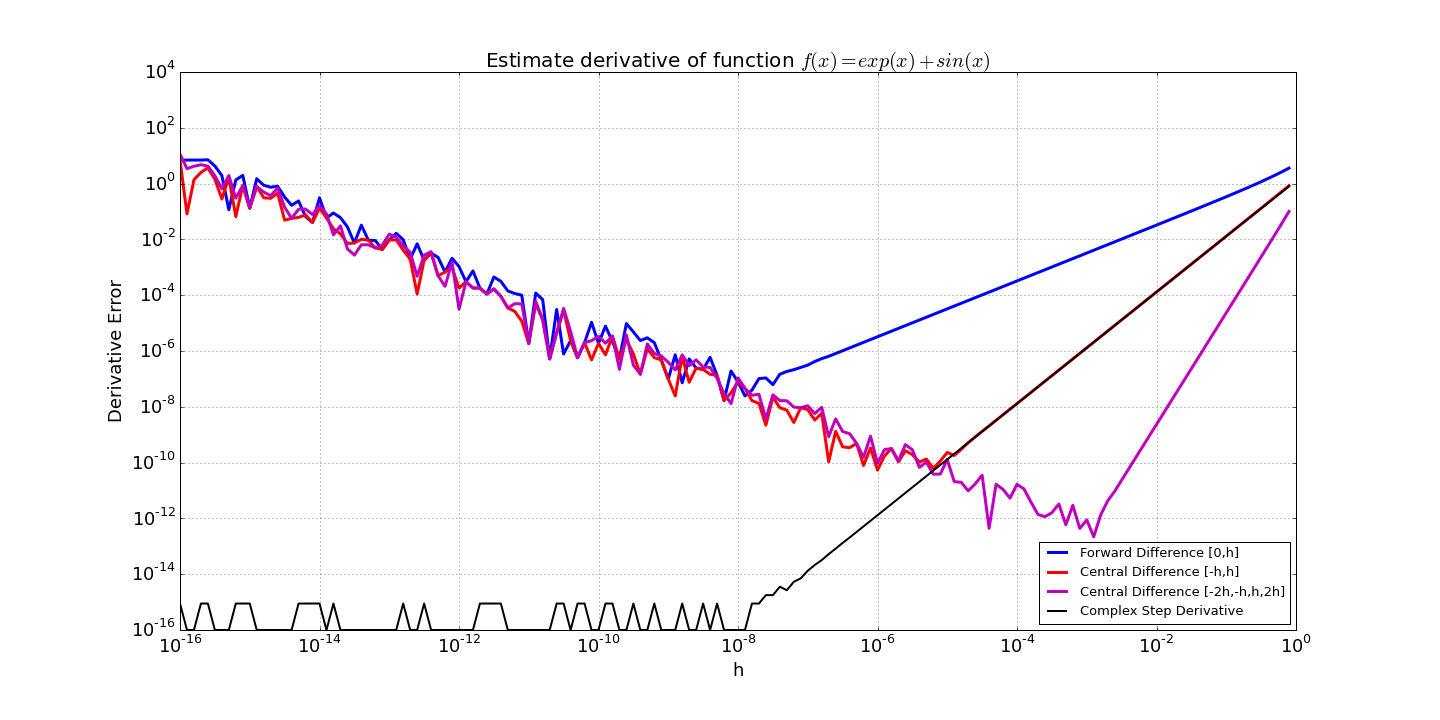
Typically, each variable \(x_i\) is perturbed by a value \(h_i\) using forward, backward, or central differences to compute the Jacobian one column at a time (\(\partial \mathbf{f} / \partial x_i\)). Higher-order methods are also possible [1]. The following finite difference formulas are currently available in the library:
- Two points:
- \((f(x+h)-f(x)) / h\)
- \((f(x)-f(x-h)) / h\)
- Three points:
- \((f(x+h)-f(x-h)) / (2h)\)
- \((-3f(x)+4f(x+h)-f(x+2h)) / (2h)\)
- \((f(x-2h)-4f(x-h)+3f(x)) / (2h)\)
- Four points:
- \((-2f(x-h)-3f(x)+6f(x+h)-f(x+2h)) / (6h)\)
- \((f(x-2h)-6f(x-h)+3f(x)+2f(x+h)) / (6h)\)
- \((-11f(x)+18f(x+h)-9f(x+2h)+2f(x+3h)) / (6h)\)
- \((-2f(x-3h)+9f(x-2h)-18f(x-h)+11f(x)) / (6h)\)
- Five points:
- \((f(x-2h)-8f(x-h)+8f(x+h)-f(x+2h)) / (12h)\)
- \((-3f(x-h)-10f(x)+18f(x+h)-6f(x+2h)+f(x+3h)) / (12h)\)
- \((-f(x-3h)+6f(x-2h)-18f(x-h)+10f(x)+3f(x+h)) / (12h)\)
- \((-25f(x)+48f(x+h)-36f(x+2h)+16f(x+3h)-3f(x+4h)) / (12h)\)
- \((3f(x-4h)-16f(x-3h)+36f(x-2h)-48f(x-h)+25f(x)) / (12h)\)
The basic features of NumDiff are listed here:
- A variety of finite difference methods are available (and it is easy to add new ones).
- If you want, you can specify a different finite difference method to use to compute each column of the Jacobian.
- You can also specify the number of points of the methods, and a suitable one of that order will be selected on-the-fly so as not to violate the variable bounds.
- I also included an alternate method using Neville's process which computes each element of the Jacobian individually [2]. It takes a very large number of function evaluations but produces the most accurate answer.
- A hash table based caching system is implemented to cache function evaluations to avoid unnecessary function calls if they are not necessary.
- It supports very large sparse systems by compactly storing and computing the Jacobian matrix using the sparsity pattern. Optimization codes such as SNOPT and Ipopt can use this form.
- It can also return the dense (\(m \times n\)) matrix representation of the Jacobian if that sort of thing is your bag (for example, the older SLSQP requires this form).
- It can also return the \(J*v\) product, where \(J\) is the full (\(m \times n\)) Jacobian matrix and v is an (\(n \times 1\)) input vector. This is used for Krylov type algorithms.
- The sparsity pattern can be supplied by the user or computed by the library.
- The sparsity pattern can also be partitioned so as compute multiple columns of the Jacobian simultaneously so as to reduce the number of function calls [3].
- It is written in object-oriented Fortran 2008. All user interaction is through a NumDiff class.
- It is open source with a BSD-3 license.
I haven't yet really tried to fine-tune the code, so I make no claim that it is the most optimal it could be. I'm using various modern Fortran vector and matrix intrinsic routines such as PACK, COUNT, etc. Likely there is room for efficiency improvements. I'd also like to add some parallelization, either using OpenMP or Coarray Fortran. OpenMP seems to have some issues with some modern Fortran constructs so that might be tricky. I keep meaning to do something real with coarrays, so this could be my chance.
So, there you go internet. If anybody else finds it useful, let me know.
References
- G. Engeln-Müllges, F. Uhlig, Numerical Algorithms with Fortran, Springer-Verlag Berlin Heidelberg, 1996.
- J. Oliver, "An algorithm for numerical differentiation of a function of one real variable", Journal of Computational and Applied Mathematics 6 (2) (1980) 145–160. [A Fortran 77 implementation of this algorithm by David Kahaner was formerly available from NIST, but the link seems to be dead. My modern Fortran version is available here.]
- T. F. Coleman, B. S. Garbow, J. J. Moré, "Algorithm 618: FORTRAN subroutines for estimating sparse Jacobian Matrices", ACM Transactions on Mathematical Software (TOMS), Volume 10 Issue 3, Sept. 1984.