Jan 27, 2018
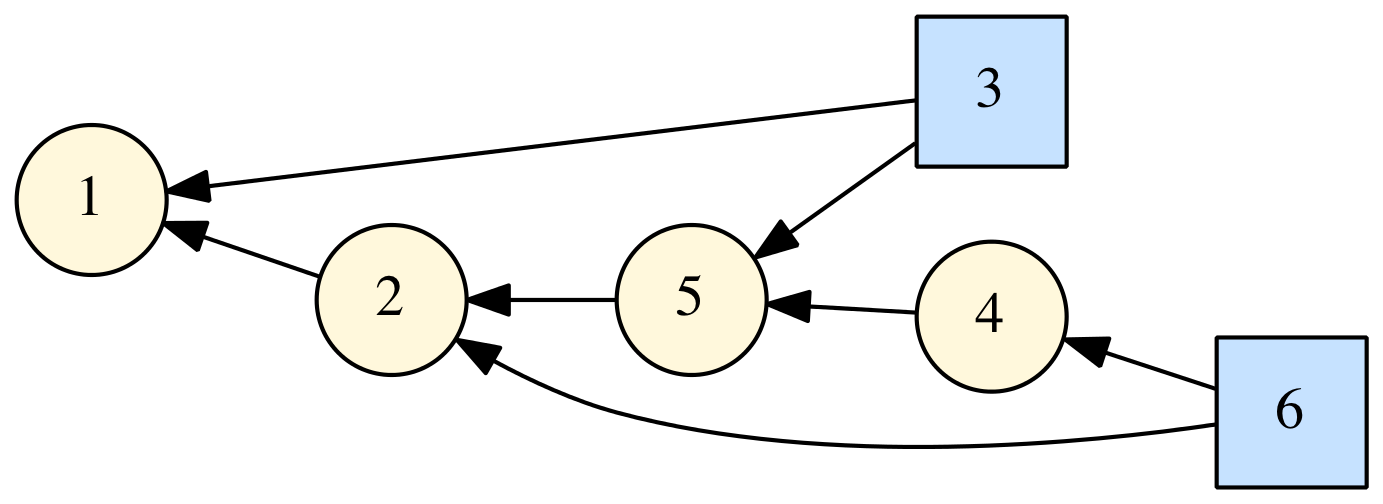
I released a new open source project on GitHub: DAGLIB, a modern Fortran library for manipulation of directed acyclic graphs (DAGs). This is based on some code I showed in a previous post. Right now, it's very basic, but you can use it to define DAGs, generate the topologically sorted order, and generate a "dot" file that can be used by GraphViz to visualize the DAG (such as the one shown at right).
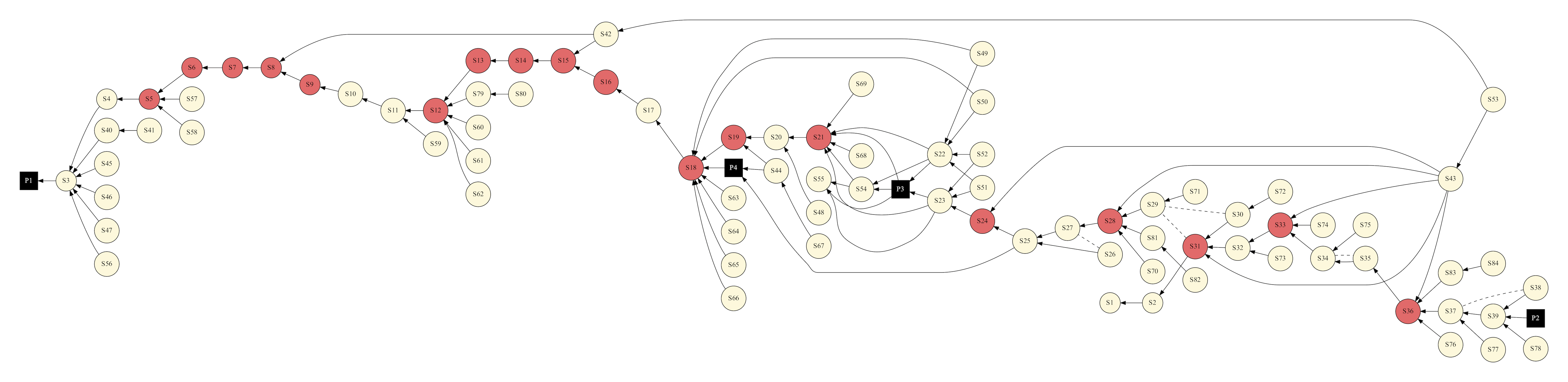
In my recent AIAA paper I showed the following DAG representing how we have designed the upcoming Orion EM-1 mission:

*During Exploration Mission-1, Orion will venture thousands of miles beyond the moon during an approximately three week mission. [NASA]*
In this case, the DAG represents the dependencies among different mission attributes (which represent maneuvers, coast phases, constraints, other algorithms, etc). To simulate the entire end-to-end mission, each element must be evaluated in the correct order such that all the dependencies are met. In this same paper, we also discuss other algorithms and their implementation in modern Fortran which may be familiar to readers of this blog.
See also
- J. Williams, R. D. Falck, and I. B. Beekman. "Application of Modern Fortran to Spacecraft Trajectory Design and Optimization", 2018 Space Flight Mechanics Meeting, AIAA SciTech Forum, (AIAA 2018-1451)
- (Modern?) Fortran directed graphs library [comp.lang.fortran] May 6, 2016
- JSON-Fortran GraphViz Example (how to generate a directed graph from a JSON structure), Apr 22, 2017
- The Ins and Outs of NASA’s First Launch of SLS and Orion, NASA, Nov. 27, 2015
Mar 05, 2017
I just released some updates to my two most popular Fortran libraries on GitHub: JSON-Fortran and bspline-fortran. Coincidently, both are now at v5.2.0. Details of the updates are:
JSON-Fortran

There are several new features in this release. The biggest update is that now the code can parse JSON files that include comments (it just ignores them). You can even specify the character that identifies a comment. For example, if using # as a comment character, the following file can now be parsed just fine:
{
"t": 0.12345, # this is the time
"x": 123.7173 # this is the state
}
Technically, comments are not part of the JSON standard. Douglas Crockford, the creator of JSON, had his reasons [1] for not including them, which I admit I don't understand (something about parsing directives and interoperability?) I mainly use JSON for configuration files, where it is nice to have comments. Crockford's suggestion for this use case is to pipe your commented JSON files through something called JSMin before parsing, a solution which seems somewhat ridiculous for Fortran users. So, never fear, now we can have comments in our JSON files and continue not using JavaScript for anything.
Another big change is the addition of support for the RFC 6901 "JSON Pointer" path specification [2]. This can be used to retrieve data from a JSON structure using its path. Formerly, JSON-Fortran used a simple path specification syntax, which broke down if the keys contained special characters such as ( or ). The new way works for all keys.
Bspline-Fortran
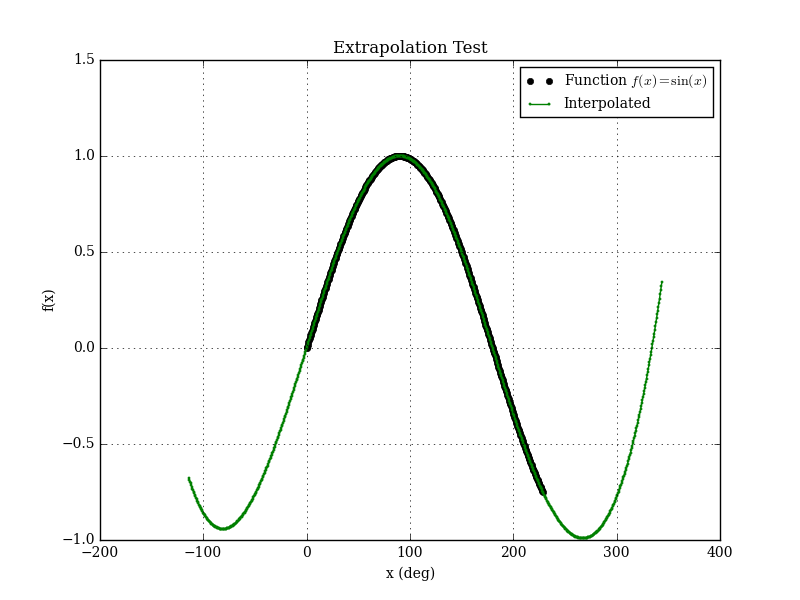
A minor update to Bspline-Fortran is the addition of an extrapolation mode. Formerly, if an interpolation was requested outside the bounds of the data, an error was returned. Now, the user has the option of enabling extrapolation.
See also
- D. Crockford, "Comments in JSON", Apr 30, 2012 [Google Plus]
- JavaScript Object Notation (JSON) Pointer, RFC 6901, April 2013 [IETF]
Feb 12, 2017

The lowly CSV (comma-separated values) file never gets any respect. Sure, it isn't really standardized, but it is a very useful text file format for columns of data, and is frequently encountered in science/engineering fields. Of course, there is no good modern Fortran library for reading and writing CSV files (see [1-2] for some older Fortran 90 code for writing only). Searching the internet (e.g., [3-4]) you will find various ad hoc suggestions for handling these files. It's amazing how little Fortran users expect their language to support non-numerical algorithms. No Fortran programmer would ever suggest that someone roll their own matrix inverse routine, but they don't see anything wrong with having to write their own data file parser (if you told a Python user they had to write their own CSV parser, you'd be laughed out of the place).
So, I created fortran-csv-module (now available on GitHub), a modern Fortran library for reading and writing CSV files. Everything is handled by an object-oriented csv_file class. Here is an example for writing a file:
program csv_write_test
use csv_module
use iso_fortran_env, only: wp => real64
implicit none
type(csv_file) :: f
logical :: status_ok
! open the file
call f%open('test.csv',n_cols=4,status_ok=status_ok)
! add header
call f%add(['x','y','z','t'])
call f%next_row()
! add some data:
call f%add([1.0_wp,2.0_wp,3.0_wp],real_fmt='(F5.3)')
call f%add(.true.)
call f%next_row()
call f%add([4.0_wp,5.0_wp,6.0_wp],real_fmt='(F5.3)')
call f%add(.false.)
call f%next_row()
! finished
call f%close(status_ok)
end program csv_write_test
Which produces the following file:
x,y,z,t 1.000,2.000,3.000,T 4.000,5.000,6.000,F
Real, integer, logical, or character data can be added as scalars, vectors, and matrices.
When reading a CSV file, the data is stored internally in the class as allocatable character strings, which can be retrieved as real, integer, logical or character vectors as necessary. For example, to get the x, y, z, and t vectors from the previously-generated file:
program csv_read_test
use csv_module
use iso_fortran_env, only: wp => real64
implicit none
type(csv_file) :: f
character(len=30),dimension(:),allocatable :: header
real(wp),dimension(:),allocatable :: x,y,z
logical,dimension(:),allocatable :: t
logical :: status_ok
integer,dimension(:),allocatable :: itypes
! read the file
call f%read('test.csv',header_row=1,status_ok=status_ok)
! get the header and type info
call f%get_header(header,status_ok)
call f%variable_types(itypes,status_ok)
! get some data
call f%get(1,x,status_ok)
call f%get(2,y,status_ok)
call f%get(3,z,status_ok)
call f%get(4,t,status_ok)
! destroy the file
call f%destroy()
end program csv_read_test
Various options are user-selectable for specifying the format (e.g., changing the quote or delimiter characters). You can choose to enclose strings (or all fields) in quotes or not. The library works pretty well, and there are probably additional improvements that could be made. For one thing, it doesn't properly handle the case of a string that contains the delimiter character (I'll eventually fix this). If anybody has any other improvements, fork it and send me a pull request. The license is BSD, so you can use it for whatever you want.
See also
- J. Burkardt, CSV_IO -- Read and Write Comma Separated Values (CSV) Files. [note: it doesn't actually contain any CSV reading capability]
- A. Markus, FLIBS -- Includes a csv_file module for writing CSV files.
- How to read a general csv file [Intel Fortran Forum]
- Read data from a .csv file in fortran [Stack Overflow]
Dec 12, 2016
In an earlier post, I mentioned that we needed an object-oriented modern Fortran library for multidimensional linear interpolation. Well, here it is. I call it finterp, and it is available on GitHub. It can be used for 1D-6D interpolation/extrapolation of data on a regular grid (i.e., not scattered). It has a similar object-oriented interface as my bspline-fortran library, with initialize, evaluate, and destroy methods like so:
type(linear_interp_3d) :: interp
call interp%initialize(xvec,yvec,zvec,fmat,iflag)
call interp%evaluate(x,y,z,f)
call interp%destroy()
For example, the low-level 3D interpolation evaluate routine is:
pure subroutine interp_3d(me,x,y,z,fxyz)
implicit none
class(linear_interp_3d),intent(inout) :: me
real(wp),intent(in) :: x
real(wp),intent(in) :: y
real(wp),intent(in) :: z
real(wp),intent(out) :: fxyz !! Interpolated ( f(x,y,z) )
integer,dimension(2) :: ix, iy, iz
real(wp) :: p1, p2, p3
real(wp) :: q1, q2, q3
integer :: mflag
real(wp) :: fx11, fx21, fx12, fx22, fxy1, fxy2
call dintrv(me%x,x,me%ilox,ix(1),ix(2),mflag)
call dintrv(me%y,y,me%iloy,iy(1),iy(2),mflag)
call dintrv(me%z,z,me%iloz,iz(1),iz(2),mflag)
q1 = (x-me%x(ix(1)))/(me%x(ix(2))-me%x(ix(1)))
q2 = (y-me%y(iy(1)))/(me%y(iy(2))-me%y(iy(1)))
q3 = (z-me%z(iz(1)))/(me%z(iz(2))-me%z(iz(1)))
p1 = one-q1
p2 = one-q2
p3 = one-q3
fx11 = p1*me%f(ix(1),iy(1),iz(1)) + q1*me%f(ix(2),iy(1),iz(1))
fx21 = p1*me%f(ix(1),iy(2),iz(1)) + q1*me%f(ix(2),iy(2),iz(1))
fx12 = p1*me%f(ix(1),iy(1),iz(2)) + q1*me%f(ix(2),iy(1),iz(2))
fx22 = p1*me%f(ix(1),iy(2),iz(2)) + q1*me%f(ix(2),iy(2),iz(2))
fxy1 = p2*( fx11 ) + q2*( fx21 )
fxy2 = p2*( fx12 ) + q2*( fx22 )
fxyz = p3*( fxy1 ) + q3*( fxy2 )
end subroutine interp_3d
The finterp library is released under a permissive BSD-3 license. As far as I can tell, it is unique among publicly-available Fortran codes in providing linear interpolation for up to 6D data sets. There used to be a Fortran 77 library called REGRIDPACK for regridding 1D-4D data sets (it had the option to use linear or cubic interpolation independently for each dimension). Written by John C. Adams at the National Center for Atmospheric Research in 1999, it used to be hosted at the UCAR website, but the link is now dead. You can still find it on the internet though, as part of other projects (for example here, where it is being used via a Python wrapper). But the licensing is unclear to me.
The dearth of easy-to-find, easy-to-use, high-quality open source modern Fortran libraries is a big problem for the long-term future of the language. Fortran users don't seem to be as interested in promoting their language as users of some of the newer programming languages are. There is a group of us working to change this, but we've got a long way to go. For example, Julia, a programming language only four years old, already has a ton of libraries, some of which are just wrappers to Fortran 77 code that no one's ever bothered to modernize. They even have a yearly conference. An in depth article about this state of affairs is a post for another day.
References
Dec 04, 2016

I present the initial release of a new modern Fortran library for computing Jacobian matrices using numerical differentiation. It is called NumDiff and is available on GitHub. The Jacobian is the matrix of partial derivatives of a set of \(m\) functions with respect to \(n\) variables:
$$
\mathbf{J}(\mathbf{x}) = \frac{d \mathbf{f}}{d \mathbf{x}} = \left[
\begin{array}{ c c c }
\frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\
\vdots & \ddots & \vdots \\
\frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \\
\end{array}
\right]
$$
Typically, each variable \(x_i\) is perturbed by a value \(h_i\) using forward, backward, or central differences to compute the Jacobian one column at a time (\(\partial \mathbf{f} / \partial x_i\)). Higher-order methods are also possible [1]. The following finite difference formulas are currently available in the library:
- Two points:
- \((f(x+h)-f(x)) / h\)
- \((f(x)-f(x-h)) / h\)
- Three points:
- \((f(x+h)-f(x-h)) / (2h)\)
- \((-3f(x)+4f(x+h)-f(x+2h)) / (2h)\)
- \((f(x-2h)-4f(x-h)+3f(x)) / (2h)\)
- Four points:
- \((-2f(x-h)-3f(x)+6f(x+h)-f(x+2h)) / (6h)\)
- \((f(x-2h)-6f(x-h)+3f(x)+2f(x+h)) / (6h)\)
- \((-11f(x)+18f(x+h)-9f(x+2h)+2f(x+3h)) / (6h)\)
- \((-2f(x-3h)+9f(x-2h)-18f(x-h)+11f(x)) / (6h)\)
- Five points:
- \((f(x-2h)-8f(x-h)+8f(x+h)-f(x+2h)) / (12h)\)
- \((-3f(x-h)-10f(x)+18f(x+h)-6f(x+2h)+f(x+3h)) / (12h)\)
- \((-f(x-3h)+6f(x-2h)-18f(x-h)+10f(x)+3f(x+h)) / (12h)\)
- \((-25f(x)+48f(x+h)-36f(x+2h)+16f(x+3h)-3f(x+4h)) / (12h)\)
- \((3f(x-4h)-16f(x-3h)+36f(x-2h)-48f(x-h)+25f(x)) / (12h)\)
The basic features of NumDiff are listed here:
- A variety of finite difference methods are available (and it is easy to add new ones).
- If you want, you can specify a different finite difference method to use to compute each column of the Jacobian.
- You can also specify the number of points of the methods, and a suitable one of that order will be selected on-the-fly so as not to violate the variable bounds.
- I also included an alternate method using Neville's process which computes each element of the Jacobian individually [2]. It takes a very large number of function evaluations but produces the most accurate answer.
- A hash table based caching system is implemented to cache function evaluations to avoid unnecessary function calls if they are not necessary.
- It supports very large sparse systems by compactly storing and computing the Jacobian matrix using the sparsity pattern. Optimization codes such as SNOPT and Ipopt can use this form.
- It can also return the dense (\(m \times n\)) matrix representation of the Jacobian if that sort of thing is your bag (for example, the older SLSQP requires this form).
- It can also return the \(J*v\) product, where \(J\) is the full (\(m \times n\)) Jacobian matrix and v is an (\(n \times 1\)) input vector. This is used for Krylov type algorithms.
- The sparsity pattern can be supplied by the user or computed by the library.
- The sparsity pattern can also be partitioned so as compute multiple columns of the Jacobian simultaneously so as to reduce the number of function calls [3].
- It is written in object-oriented Fortran 2008. All user interaction is through a NumDiff class.
- It is open source with a BSD-3 license.
I haven't yet really tried to fine-tune the code, so I make no claim that it is the most optimal it could be. I'm using various modern Fortran vector and matrix intrinsic routines such as PACK, COUNT, etc. Likely there is room for efficiency improvements. I'd also like to add some parallelization, either using OpenMP or Coarray Fortran. OpenMP seems to have some issues with some modern Fortran constructs so that might be tricky. I keep meaning to do something real with coarrays, so this could be my chance.
So, there you go internet. If anybody else finds it useful, let me know.
References
- G. Engeln-Müllges, F. Uhlig, Numerical Algorithms with Fortran, Springer-Verlag Berlin Heidelberg, 1996.
- J. Oliver, "An algorithm for numerical differentiation of a function of one real variable", Journal of Computational and Applied Mathematics 6 (2) (1980) 145–160. [A Fortran 77 implementation of this algorithm by David Kahaner was formerly available from NIST, but the link seems to be dead. My modern Fortran version is available here.]
- T. F. Coleman, B. S. Garbow, J. J. Moré, "Algorithm 618: FORTRAN subroutines for estimating sparse Jacobian Matrices", ACM Transactions on Mathematical Software (TOMS), Volume 10 Issue 3, Sept. 1984.
May 30, 2016
Sorting is one of the fundamental problems in computer science, so of course Fortran does not include any intrinsic sorting routine (we've got Bessel functions, though!) String sorting is a special case of this problem which includes various choices to consider, for example:
- Natural or ASCII sorting
- Case sensitive (e.g., 'A'<'a') or case insensitive (e.g., 'A'=='a')
"Natural" sorting (also called "alphanumeric sorting" means to take into account numeric values in the string, rather than just comparing the ASCII value of each of the characters. This can produce an order that looks more natural to a human for strings that contain numbers. For example, in a "natural" sort, the string "case2.txt" will come before "case100.txt", since the number 2 comes before the number 100. For example, natural sorting is the method used to sort file names in the MacOS X Finder (see image at right). While, interestingly, an ls -l from a Terminal merely does a basic ASCII sort.
For string sorting routines written in modern Fortran, check out my GitHub project stringsort. This library contains routines for both natural and ASCII string sorting. Natural sorting is achieved by breaking up each string into chunks. A chunk consists of a non-numeric character or a contiguous block of integer characters. A case insensitive search is done by simply converting each character to lowercase before comparing them. I make no claim that the routines are particularly optimized. One limitation is that contiguous integer characters are stored as an integer(INT32) value, which has a maximum value of 2147483647. Although note that it is easy to change the code to use integer(INT64) variables to increase this range up to 9223372036854775807 if necessary. Eliminating integer size restrictions entirely is left as an exercise for the reader.
Consider the following test case:
character(len=*),dimension(6) :: &
str = [ 'z1.txt ', &
'z102.txt', &
'Z101.txt', &
'z100.txt', &
'z10.txt ', &
'Z11.txt ' ]
This list can be sorted (at least) four different ways:
Case Insensitive
ASCII
z1.txt
z10.txt
z100.txt
Z101.txt
z102.txt
Z11.txt
natural
z1.txt
z10.txt
Z11.txt
z100.txt
Z101.txt
z102.txt
Case Sensitive
ASCII
Z101.txt
Z11.txt
z1.txt
z10.txt
z100.txt
z102.txt
natural
Z11.txt
Z101.txt
z1.txt
z10.txt
z100.txt
z102.txt
Each of these can be done using stringsort with the following subroutine calls:
call lexical_sort_recursive(str,case_sensitive=.false.)
call lexical_sort_natural_recursive(str,case_sensitive=.false.)
call lexical_sort_recursive(str,case_sensitive=.true.)
call lexical_sort_natural_recursive(str,case_sensitive=.true.)

*Original Quicksort algorithm by Tony Hoare, 1961 (Communications of the ACM)*
The routines use the quicksort algorithm, which was originally created for sorting strings (specifically words in Russian sentences so they could be looked up in a Russian-English dictionary). The algorithm is easily implemented in modern Fortran using recursion (non-recursive versions were also available before recursion was added to the language in Fortran 90). Quicksort was named one of the top 10 algorithms of the 20th century by the ACM (Fortran was also on the list).
See also
May 12, 2016

GitHub announced yesterday that all of their paid plans now include unlimited private repositories. They've also simplified their pricing scheme, so now there is only one paid plan for individuals for \$7 per month. This now includes unlimited private repositories, and these can include collaborators.
All of my open source projects are hosted on GitHub. It's been a great way to share and collaborate on code. Now it looks like it's even better for working on stuff that you might not want to share.
Be sure to also check out the Fortran F/OSS programmers group.
May 09, 2016

JSON-Fortran 5.0 is out. This release finally brings thread-safety to the library. Note that it does break backward compatibility with previous versions, but hopefully it isn't too much trouble to modify your code to be compatible with the new release. I've provided a short guide describing what you need to do.
JSON-Fortran is a Fortran 2008 JSON API, based on an earlier project called FSON (which was written in Fortran 95). FSON was not thread-safe, and so neither was JSON-Fortran at first. This was mainly due to the use of various global settings, and global variables used during parsing and for keeping track of errors.
In the transition from FSON to JSON-Fortran, I added a high-level json_file class that is used to do a lot of common operations (e.g. open a JSON file and read data from it). However, building a JSON structure from scratch is done using lower-level json_value pointers. In the 5.0 release, there is a new factory class called json_core that is now the interface for manipulating json_value variables. Thus, each instance of this class can exist independently of any others (each with potentially different settings), and so provides thread-safe operation and error handling. The json_file class simply contains an instance of json_core, which contains all the variables and settings that were formerly global to the entire module.
A very simple example of the pre-5.0 usage would be:
program test
use json_module
implicit none
type(json_file) :: json
integer :: ival
character(len=:),allocatable :: cval
logical :: found
call json_initialize()
call json%load_file(filename='myfile.json')
call json%print_file() !print to the console
call json%get('var.i',ival,found)
call json%get('var.c',cval,found)
call json%destroy()
end program test
For 5.0, all you have to do is change:
to
and you're done. All global variables have been eliminated and the only entities that are user-accessible are three public types and their methods.
There are also a ton of other new features in JSON-Fortran 5.0, including new APIs, such as:
json_core%validate() -- test the validity of a JSON structure (i.e., a json_value linked list).json_core%is_child_of() -- test if one json_value is a child of another.json_core%swap() -- swap two json_value elements in a JSON structure (this may be useful for sorting purposes).json_core%rename() -- rename a json_value variable in a JSON structure.
And new settings (set during the call to initialize()) such as:
- Trailing spaces can now be significant for name comparisons.
- Name comparisons can now be case sensitive or case insensitive.
- Can enable strict type checking to avoid automatic conversion of numeric data (say, integer to double) when getting data from a JSON structure.
- Can set the number of spaces for indenting when writing JSON data to a file.
See also
Jan 12, 2016
SLSQP [1-2] is a sequential quadratic programming (SQP) optimization algorithm written by Dieter Kraft in the 1980s. It can be used to solve nonlinear programming problems that minimize a scalar function:
$$
f(\mathbf{x})
$$
subject to general equality and inequality constraints:
$$
\begin{array}{rl} g_j(\mathbf{x}) = \mathbf{0} & j = 1, \dots ,m_e \\
g_j(\mathbf{x}) \ge \mathbf{0} & j = m_e+1, \dots ,m \end{array}
$$
and to lower and upper bounds on the variables:
$$
\begin{array}{rl} l_i \le x_i \le u_i & i = 1, \dots ,n \end{array}
$$
SLSQP was written in Fortran 77, and is included in PyOpt (called using Python wrappers) and NLopt (as an f2c translation of the original source). It is also included as one of the solvers in two of NASA's trajectory optimization tools (OTIS and Copernicus).
The code is pretty old school and includes numerous obsolescent Fortran features such as arithmetic IF statements, computed and assigned GOTO statements, statement functions, etc. It also includes some non-standard assumptions (implicit saving of variables and initialization to zero).
So, the time is ripe for refactoring SLSQP. Which is what I've done. The refactored version includes some new features and bug fixes, including:
- It is now thread safe. The original version was not thread safe due to the use of saved variables in one of the subroutines.
- It should now be 100% standard compliant (Fortran 2008).
- It now has an easy-to-use object-oriented interface. The
slsqp_class is used for all interactions with the solver. Methods include initialize(), optimize(), and destroy().
- It includes updated versions of some of the third-party routines used in the original code (BLAS, LINPACK, and NNLS).
- It has been translated into free-form source. For this, I used the sample online version of the SPAG Fortran Code Restructuring tool to perform some of the translation, which seemed to work really well. The rest I did manually. Fixed-form source (FORTRAN 77 style) is terrible and needs to die. There's no reason to be using it 25 years after the introduction of free-form source (yes, I'm talking to you Claus 😀).
- The documentation strings in the code have been converted to FORD format, allowing for nicely formatted documentation to be auto-generated (which includes MathJax formatted equations to replace the ASCII ones in the original code). It also generates ultra-slick call graphs like the one below.
- A couple of bug fixes noted elsewhere have been applied (see here and here).
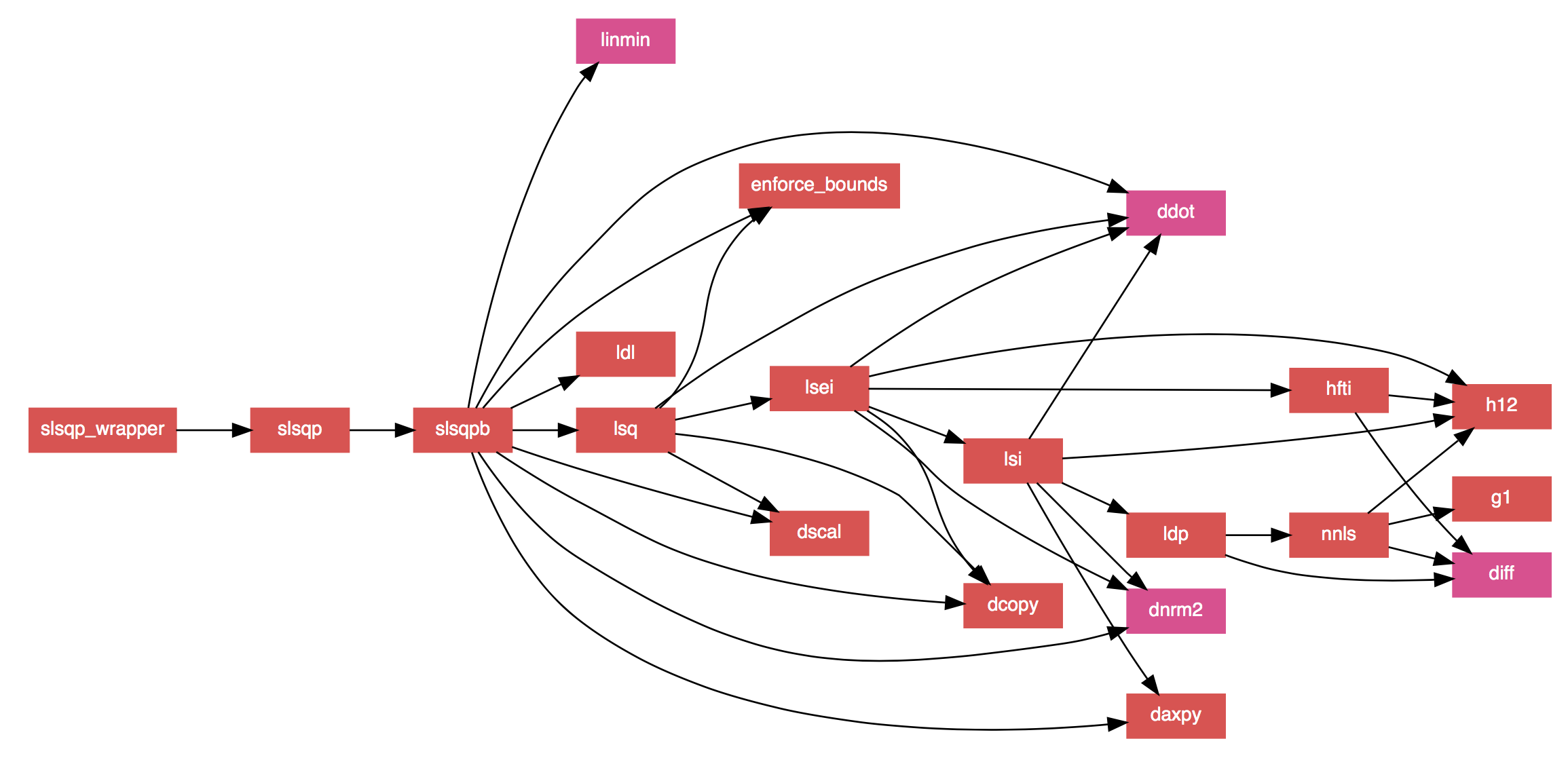
*SLSQP call graph generated by FORD.*
The original code used a "reverse communication" interface, which was one of the workarounds used in old Fortran code to make up for the fact that there wasn't really a good way to pass arbitrary data into a library routine. So, the routine returns after called, requests data, and then is called again. For now, I've kept the reverse communication interface in the core routines (the user never interacts with them directly, however). Eventually, I may do away with this, since I don't think it's particularly useful anymore.
The new code is on GitHub, and is released under a BSD license. There are various additional improvements that could be made, so I'll continue to tinker with it, but for now it seems to work fine. If anyone else finds the new version useful, I'd be interested to hear about it.
See Also
- Dieter Kraft, "A Software Package for Sequential Quadratic Programming", DFVLR-FB 88-28, 1988.
- Dieter Kraft, "Algorithm 733: TOMP–Fortran Modules for Optimal Control Calculations," ACM Transactions on Mathematical Software, Vol. 20, No. 3, p. 262-281 (1994).
Nov 06, 2015
My bspline-fortran multidimensional interpolation library is now at version 4.0. The documentation can be found here. Since I first mentioned it here, I've made many updates to this library, including:
- Added object-oriented wrappers to the core routines. The user now has the choice to use the older subroutine interface or the new object-oriented interface.
- Added a set of 1D routines (suggested by a user on GitHub). The library now works for 1D-6D data sets.
- Everything is now thread-safe for your multithreaded pleasure.
The new object-oriented interface makes it pretty easy to use from modern Fortran. The classes have only three methods (initialize, evaluate, and destroy). For example, a 3D case would look like this:
type(bspline_3d) :: s
call s%initialize(x,y,z,fcn,kx,ky,kz,iflag)
call s%evaluate(xval,yval,zval,idx,idy,idz,f,iflag)
call s%destroy()
The core routines of bspline-fortran were written in the early 1980s. Good Fortran code can live on for decades after it is written. While this is great, it also means that there is a lot of old Fortran code out there that is written in a coding style that no modern programmer should accept. This can be OK for well documented library routines that the user never needs to change (see, for example SPICE or LAPACK). However, refactoring old code using modern concepts can provide many advantages, as is demonstrated in this case.
See also
- DBSPLIN and DTENSBS from the NIST Core Math Library.
- Carl de Boor, A Practical Guide to Splines, Springer-Verlag, New York, 1978.












