Gooding Universal Elements
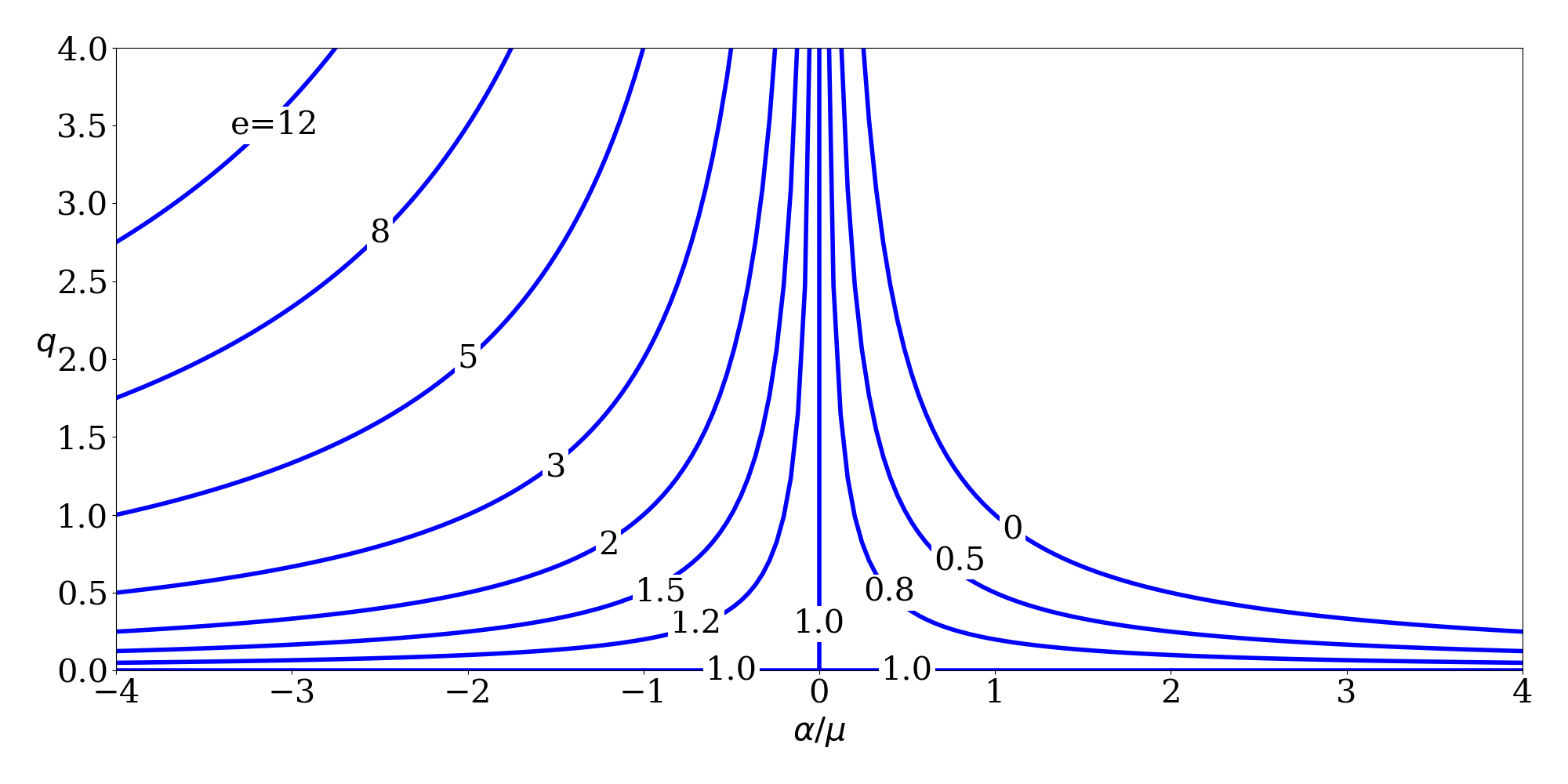
There are various different 6-element sets that can be used to represent the state (position and velocity) of a spacecraft. The classical Keplerian element set (\(a\), \(e\), \(i\), \(\Omega\), \(\omega\), \(\nu\)) is perhaps the most common, but not the only one. The Gooding universal element set [1] is:
- \(\alpha\) : twice the negative energy per unit mass (\(2 \mu / r - v^2\) or \(\mu/a\))
- \(q\) : periapsis radius magnitude (a.k.a. \(r_p\))
- \(i\) : inclination
- \(\Omega\) : right ascension of the ascending node
- \(\omega\) : argument of periapsis
- \(\tau\) : time since last periapsis passage
The nice thing about this set is that it is always defined, even for parabolas and rectilinear orbits (which other orbital element sets tend to ignore). A table from [1] shows the relationship between \(\alpha\) and \(q\) for the different types of conics:
| \(\alpha > 0\) | \(\alpha = 0\) | \(\alpha < 0\) | |
|---|---|---|---|
| \(q > 0\) | general ellipse | general parabola | general hyperbola |
| \(q = 0\) | rectilinear ellipse | rectilinear parabola | rectilinear hyperbola |
One advantage of this formulation is for trajectory optimization purposes, since if \(\alpha\) is an optimization variable, the orbit can transition from an ellipse to a hyperbola while iterating without encountering any singularities (which is not true if semimajor axis and eccentricity are being used, since \(a \rightarrow \infty\) for a parabola and then becomes negative for a hyperbola).
Gooding's original paper from 1988 includes Fortran 77 code for the transformations to and from position and velocity, coded with great care to avoid loss of accuracy due to numerical issues. Two other papers [2-3] also include some components of the algorithm. Modernized versions of these routines can be found in the Fortran Astrodynamics Toolkit. For example, a modernized version of ekepl1 (from [2]) for solving Kepler's equation:
pure function ekepl1(em, e)
!! Solve kepler's equation, `em = ekepl - e*sin(ekepl)`,
!! with legendre-based starter and halley iterator
implicit none
real(wp) :: ekepl1
real(wp),intent(in) :: em
real(wp),intent(in) :: e
real(wp) :: c,s,psi,xi,eta,fd,fdd,f
real(wp),parameter :: testsq = 1.0e-8_wp
c = e*cos(em)
s = e*sin(em)
psi = s/sqrt(1.0_wp - c - c + e*e)
do
xi = cos(psi)
eta = sin(psi)
fd = (1.0_wp - c*xi) + s*eta
fdd = c*eta + s*xi
f = psi - fdd
psi = psi - f*fd/(fd*fd - 0.5_wp*f*fdd)
if (f*f < testsq) exit
end do
ekepl1 = em + psi
end function ekepl1
The Gooding universal element set can be found in NASA's Copernicus tool, and is being used in the design and optimization of the Artemis I trajectory.
See also
- Lambert's Problem [degenerateconic.com]
- gooding_module in Fortran Astrodynamics Toolkit
References
- R. H. Gooding, "On universal elements, and conversion procedures to and from position and velocity" Celestial Mechanics 44 (1988), 283-298.
- A. W. Odell, R. H. Gooding, "Procedures for solving Kepler's equation" Celestial Mechanics 38 (1986), 307-334.
- R. H. Gooding, A. W. Odell. "The hyperbolic Kepler equation (and the elliptic equation revisited)" Celestial Mechanics 44 (1988), 267-282.
- J, Williams, J. S. Senent, and D. E. Lee, "Recent improvements to the copernicus trajectory design and optimization system", Advances in the Astronautical Sciences 143, January 2012 (AAS 12-236)
- G. Hintz, "Survey of Orbit Element Sets", Journal of Guidance Control and Dynamics, 31(3):785-790, May 2008