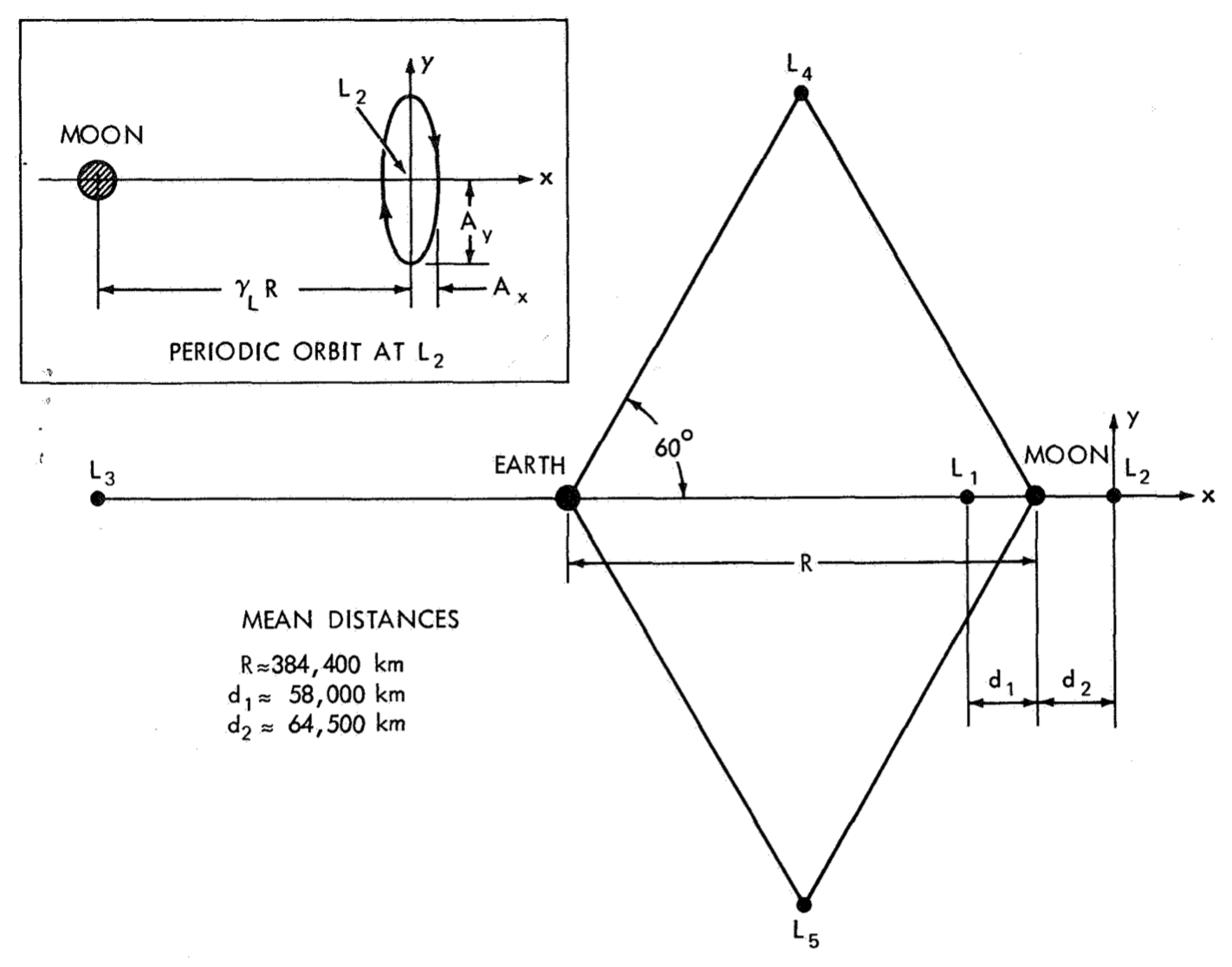
Circular Restricted Three-Body Problem
The Circular Restricted Three-Body Problem (CR3BP) is a continuing source of delight for astrodynamicists. If you think that, after 200 years, everything that could ever be written about this subject has already been written, you would be wrong. The basic premise is to describe the motion of a spacecraft in the vicinity of two celestial bodies that are in circular orbits about their common barycenter. The "restricted" part means that the spacecraft does not affect the motion of the other two bodies (i.e., its mass is negligible).
The normalized equations of motion for the CR3BP are very simple (see the Fortran Astrodynamics Toolkit):
subroutine crtbp_derivs(mu,x,dx)
implicit none
real(wp),intent(in) :: mu
!! CRTBP parameter
real(wp),dimension(6),intent(in) :: x
!! normalized state [r,v]
real(wp),dimension(6),intent(out) :: dx
!! normalized state derivative [rdot,vdot]
real(wp),dimension(3) :: r1,r2,rb1,rb2,r,v,g
real(wp) :: r13,r23,omm,c1,c2
r = x(1:3) ! position
v = x(4:6) ! velocity
omm = one - mu
rb1 = [-mu,zero,zero] ! location of body 1
rb2 = [omm,zero,zero] ! location of body 2
r1 = r - rb1 ! body1 -> sc vector
r2 = r - rb2 ! body2 -> sc vector
r13 = norm2(r1)**3
r23 = norm2(r2)**3
c1 = omm/r13
c2 = mu/r23
!normalized gravity from both bodies:
g(1) = -c1*(r(1) + mu) - c2*(r(1)-one+mu)
g(2) = -c1*r(2) - c2*r(2)
g(3) = -c1*r(3) - c2*r(3)
! derivative of x:
dx(1:3) = v ! rdot
dx(4) = two*v(2) + r(1) + g(1) ! vdot
dx(5) = -two*v(1) + r(2) + g(2) !
dx(6) = g(3) !
end subroutine crtbp_derivs
There are many types of interesting periodic orbits that exist in this system. I've mentioned Distant Retrograde Orbits (DROs) here before. Probably the most well-known CR3BP periodic orbits are called "halo orbits". Halo orbits can be computed in a similar manner as DROs (see previous post). For halos, we can get a good initial guess using an analytic approximation, and then use this guess to target the real thing. See the halo orbit module in the Fortran Astrodynamics Toolkit for an example of this approach. We can also use a continuation type method to generate families of orbits (say, for the L2 libration point, we have a range of halo orbits from near-planars that "orbit" L2, to near-rectilinears with close approaches to the secondary body). In a realistic force model (with the real ephemeris of the Earth, Moon, and Sun), the orbits generated using CR3BP assumptions are not periodic, but we can use the CR3BP solution as an initial guess in a multiple-shooting type approach with a numerical nonlinear equation solver to generate quasi-periodic multi-rev solutions. See the references below for details.
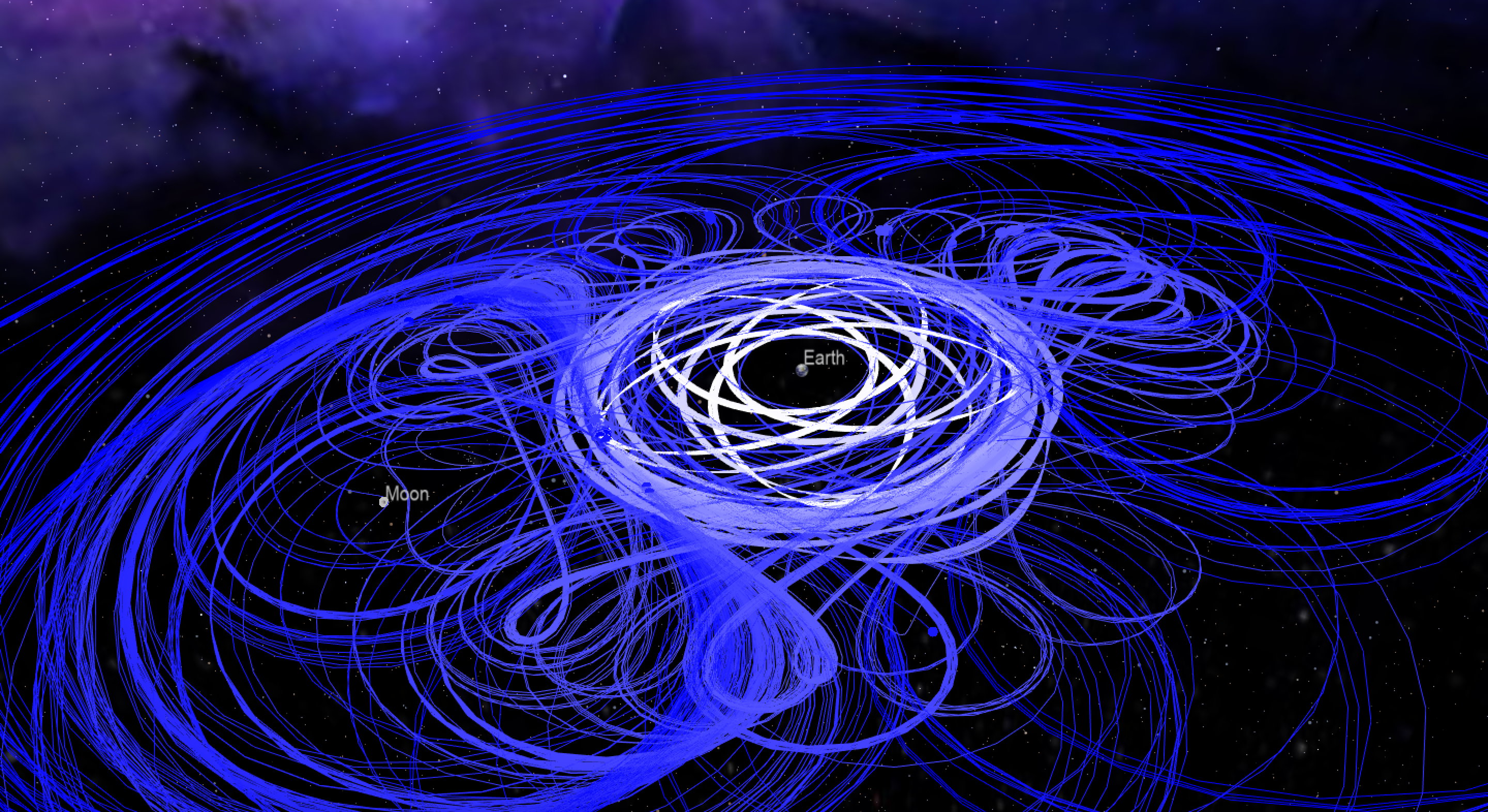
I generated the following image of a bunch of planar periodic CR3BP orbits using a program incorporating the Fortran Astrodynamics Toolkit and OpenFrames (an interface to the open source OpenSceneGraph library that can be used to visualize spacecraft trajectories). The initial states for the various orbits were taken from this database. Eventually, I will make this program open source when it is finished. There's also an online CR3BP propagator here.
See also
- M. Henon, "Numerical Exploration of the Restricted Problem. V. Hill’s Case: Periodic Orbits and Their Stability," Astronomy and Astrophys. Vol 1, 223-238, 1969.
- R. W. Farquhar, "The Utilization of Halo Orbits in Advanced Lunar Operation", NASA TN-D-6365, July 1971.
- D. L. Richardson, "Analytic Construction of Periodic Orbits About the Collinear Points", Celestial Mechanics 22 (1980)
- R. Mathur, C. A. Ocampo, "An Architecture for Incorporating Interactive Visualizations Into Scientific Simulations", 57th International Astronautical Congress, Valencia, Spain. IAC-06-D1.P.1.6.
- R. L. Restrepo, R. P. Russell, "A Database of Planar Axi-Symmetric Periodic Orbits for the Solar System," Paper AAS 17-694, AAS/AIAA Astrodynamics Specialist Conference, Stevenson, WA, Aug 2017.
- J. Williams, D. E. Lee, R. J. Whitley, K. A. Bokelmann, D. C. Davis, and C. F. Berry. "Targeting cislunar near rectilinear halo orbits for human space exploration", AAS 17-267
- Nabla Zero Labs, The Circular Restricted Three Body Problem.
- D. Davis, Near Rectilinear Halo Orbits Explained and Visualized, a.i. solutions, Jul 28, 2017 [YouTube]