Just in case you find yourself needing to do some multidimensional data interpolation with modern Fortran:
- I just published a modernized version of REGRIDPACK, a library for "regriding" 1D-4D data sets using linear and spline interpolation. The original version of this library (which used to be called TLCPACK) was formerly available from the UCAR website, but it is now nowhere to be seen. It was a well-written library, and had the nice feature of being able to specify linear or spline interpolation independently for each dimension. My refactoring is simply an update of the old code to modern standards.
- I also recently added nearest neighbor interpolation to my Finterp library. So, now you can perform linear and nearest neighbor interpolation/extrapolation on 1D-6D data sets.
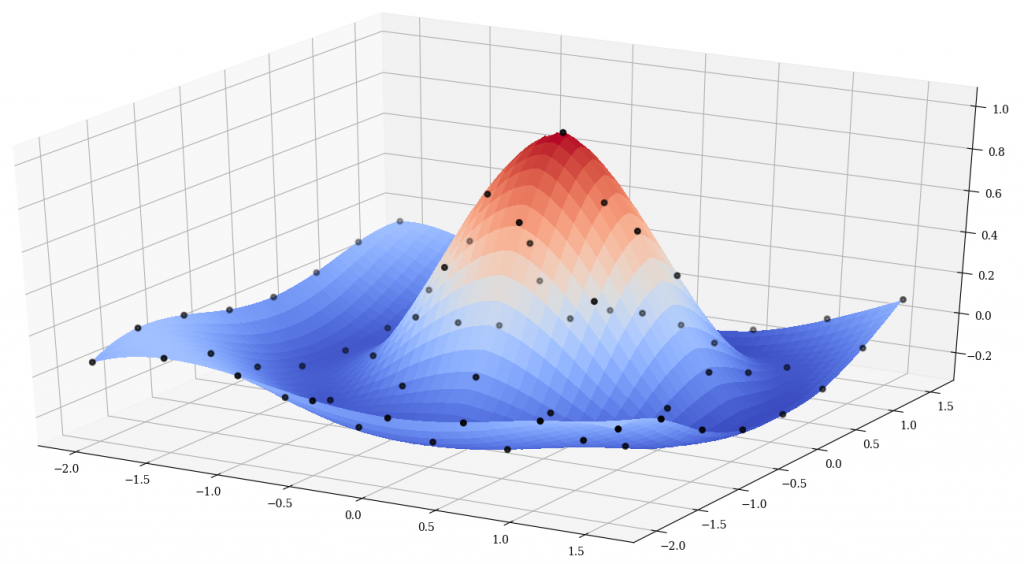
- My Bspline-Fortran library can also be used for interpolation/extrapolation of 1D-6D data sets using B-splines. This library is being used by several people for CFD work, it seems.
There are precious few modern Fortran libraries for other types of interpolation. Here are a couple:
- FOLLIA -- Fortran Library for Lagrange Interpolation
- curvefit -- A library for fitting functions to sets of data.
There are also any number of old school FORTRAN 77 codes out there that haven't been updated in decades, but still work fine for what they do, including:
- PCHIP -- Piecewise Cubic Hermite Interpolation Package from SLATEC.
- PPPACK -- Piecewise polynomial interpolation code from from A Practical Guide to Splines by C. de Boor.
- FITPACK -- a collection of FORTRAN programs for curve and surface fitting with splines and tensor product splines.
See also
My bspline-fortran multidimensional interpolation library is now at version 4.0. The documentation can be found here. Since I first mentioned it here, I've made many updates to this library, including:
- Added object-oriented wrappers to the core routines. The user now has the choice to use the older subroutine interface or the new object-oriented interface.
- Added a set of 1D routines (suggested by a user on GitHub). The library now works for 1D-6D data sets.
- Everything is now thread-safe for your multithreaded pleasure.
The new object-oriented interface makes it pretty easy to use from modern Fortran. The classes have only three methods (initialize, evaluate, and destroy). For example, a 3D case would look like this:
type(bspline_3d) :: s
call s%initialize(x,y,z,fcn,kx,ky,kz,iflag)
call s%evaluate(xval,yval,zval,idx,idy,idz,f,iflag)
call s%destroy()
The core routines of bspline-fortran were written in the early 1980s. Good Fortran code can live on for decades after it is written. While this is great, it also means that there is a lot of old Fortran code out there that is written in a coding style that no modern programmer should accept. This can be OK for well documented library routines that the user never needs to change (see, for example SPICE or LAPACK). However, refactoring old code using modern concepts can provide many advantages, as is demonstrated in this case.
See also
- DBSPLIN and DTENSBS from the NIST Core Math Library.
- Carl de Boor, A Practical Guide to Splines, Springer-Verlag, New York, 1978.
I just started a new modern Fortran software library called bspline-fortran, which is for multidimensional (multivariate) b-spline interpolation of data defined on a regular grid. It is available on GitHub, and released under a permissive BSD-style license.
It seems impossible to find code for higher than 3D spline interpolation on the internet. Einspline only has 1D-3D, as do the NIST Core Math Library DBSPLIN and DTENSBS routines. Python's SciPy stops at 2D (Bivariate splines). At first glance, the SciPy routine map_coordinates seems to do what I want, but not really since there doesn't seem to be any way to specify the abscissa vectors (x, y, z, etc.). Note: maybe there is a way, but looking at the less-than-great documentation, the minimally-commented C code, and then reading several confusing Stack Overflow posts didn't help me much. Apparently, I'm not the only one confused by this routine.
After much searching, I finally just took the 2D and 3D NIST routines (written in 1982), refactored them significantly so I could better understand what they were doing, and then extended the algorithm into higher dimensions (which is actually quite easy to do for b-splines). The original FORTRAN 77 code was somewhat hard to follow, since it was stuffing matrices into a giant WORK vector, which required a lot of obscure bookkeeping of indices. For example, I replaced this bit of code:
IZM1 = IZ - 1
KCOLY = LEFTY - KY + 1
DO 60 K=1,KZ
I = (K-1)*KY + 1
J = IZM1 + K
WORK(J) = DBVALU(TY(KCOLY),WORK(I),KY,KY,IDY,YVAL,INBV1,WORK(IW))
60 CONTINUE
with this:
kcoly = lefty - ky + 1
do k=1,kz
temp2(k) = dbvalu(ty(kcoly:),temp1(:,k),ky,ky,idy,yval,inbv1,work)
end do
which makes it a lot easier to deal with and add the extra dimensions as necessary.
The new library contains routines for 2D, 3D, 4D, 5D, and 6D interpolation. It seems like someone else may find them useful, I don't know why they don't seem to be available anywhere else. Eventually, I'll add object-oriented wrappers for the core routines, to make them easier to use.

