The International Astronomical Union (IAU) has published a new report with their latest recommendations for the cartographic coordinates and rotational elements of planetary bodies. The new guidelines, equations, and coefficients have been updated based on the latest data (including from interplanetary missions such as MESSENGER, Dawn, Rosetta, and Stardust-NExT).
One difference from the previous reports is that the low-fidelity Earth and Moon frames have been removed "in order to avoid confusion", since high-accuracy Earth and Moon frames are available. I mentioned the IAU_EARTH and IAU_MOON frames in a previous post. They are available in SPICE and the Fortran Astrodynamics Toolkit. I think it's unfortunate that they were removed. It's true that these are not ultra-precise frames (see, for example, this tutorial from JPL). However, low-to-medium fidelity frames are still very useful for many applications, including spacecraft trajectory optimization. A frame that is good enough, is very fast to compute, is continuous and differentiable for all time, and can be implemented in a few lines of code is often preferable to having to deal with thousands of lines of SOFA or SPICE code, leap second confusion, binary kernel files, etc. that are required to get the high-accuracy frames to work.
See also
- New Coordinate Systems for Solar System Bodies, IAU Announcement ann18010, Feb 27, 2018.
- B. A. Archinal, et. al., "Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2015", Celestial Mechanics and Dynamical Astronomy, Vol 130, Number 3, Feb 23, 2018.
- "High Accuracy" Orientation and Body-fixed Frames for the Moon and Earth, NAIF/JPL, January 2018.

The IAU Standards of Fundamental Astronomy (SOFA) library implements standard models used in fundamental astronomy. Version 14 ( 2018-01-30) has just been released. According to the release notes, this update includes the following:
- Change in the copyright status of the iau_DAT routine. This is to provide for a user-supplied mechanism for updating the number of leap seconds. SOFA doesn't provide any such mechanism, but they are now allowing you to replace or modify this routine to provide your own without having to rename the routine (all other SOFA routines cannot be modified without renaming them).
- Implementation of two new categories of routines:
- Three new routines for the horizon/equatorial plane coordinates.
- iau_AE2HD — (azimuth, altitude) to (hour angle, declination)
- iau_HD2AE — (hour angle, declination) to (azimuth, altitude)
- iau_HD2PA — parallactic angle
- Six new routines dealing with gnomonic (tangent plane) projections.
- iau_TPORS — solve for tangent point, spherical
- iau_TPORV — solve for tangent point, vector
- iau_TPSTS — project tangent plane to celestial, spherical
- iau_TPSTV — project tangent plane to celestial, vector
- iau_TPXES — project celestial to tangent plane, spherical
- iau_TPXEV — project celestial to tangent plane, vector
- The Astrometry Tools Cookbook, the test program and other supporting files have also been updated.
- Other minor documentation/typographical corrections to various files.
IAU SOFA has a Fortran 77 and a C version. While this is a great resource, I do wonder why the IAU insists on using a source format for the Fortran version that was rendered obsolete 30 years ago? There's no reason for this. This is new code that is regularly kept up to date, so why not modernize it for those of us living in the 21st century?
Consider this SOFA routine:
SUBROUTINE iau_TR ( R, RT )
IMPLICIT NONE
DOUBLE PRECISION R(3,3), RT(3,3)
DOUBLE PRECISION WM(3,3)
INTEGER I, J
DO 2 I=1,3
DO 1 J=1,3
WM(I,J) = R(J,I)
1 CONTINUE
2 CONTINUE
CALL iau_CR ( WM, RT )
END SUBROUTINE iau_TR
All this is doing is transposing a 3x3 matrix. Well, since the late 1990s, to do that in Fortran all you need is:
The original routine is just awful: all caps, line numbers, CONTINUE statements, and 100% unnecessary. Unfortunately, it's code like this that gives Fortran a bad name (reinforcing the perception that Fortran is an arcane and obsolete programming language). Anyone who is compiling this code is probably using a compiler that is at least Fortran 95 compatible. Who on earth is using straight up Fortran 77 compilers at this point? So why restrict such a useful library to a programming style that is so totally out of date? I think it is even probably affecting the efficiency of the code, since the example above required using a temporary array and a function call to do what can now be done with a (presumably much more efficient) intrinsic routine. It wouldn't even be that hard to convert this code to modern Fortran style. It's just low-level math routines, it doesn't have to be object-oriented or anything fancy like that. A while back, I wrote a little Python script to merge all the SOFA files into a single Fortran module (another innovation from the 1990s) so they can take advantage of the automatic interface checking that modules provide. There are also any number of tools out that could be used to automate the fixed to free-form conversion.
See also

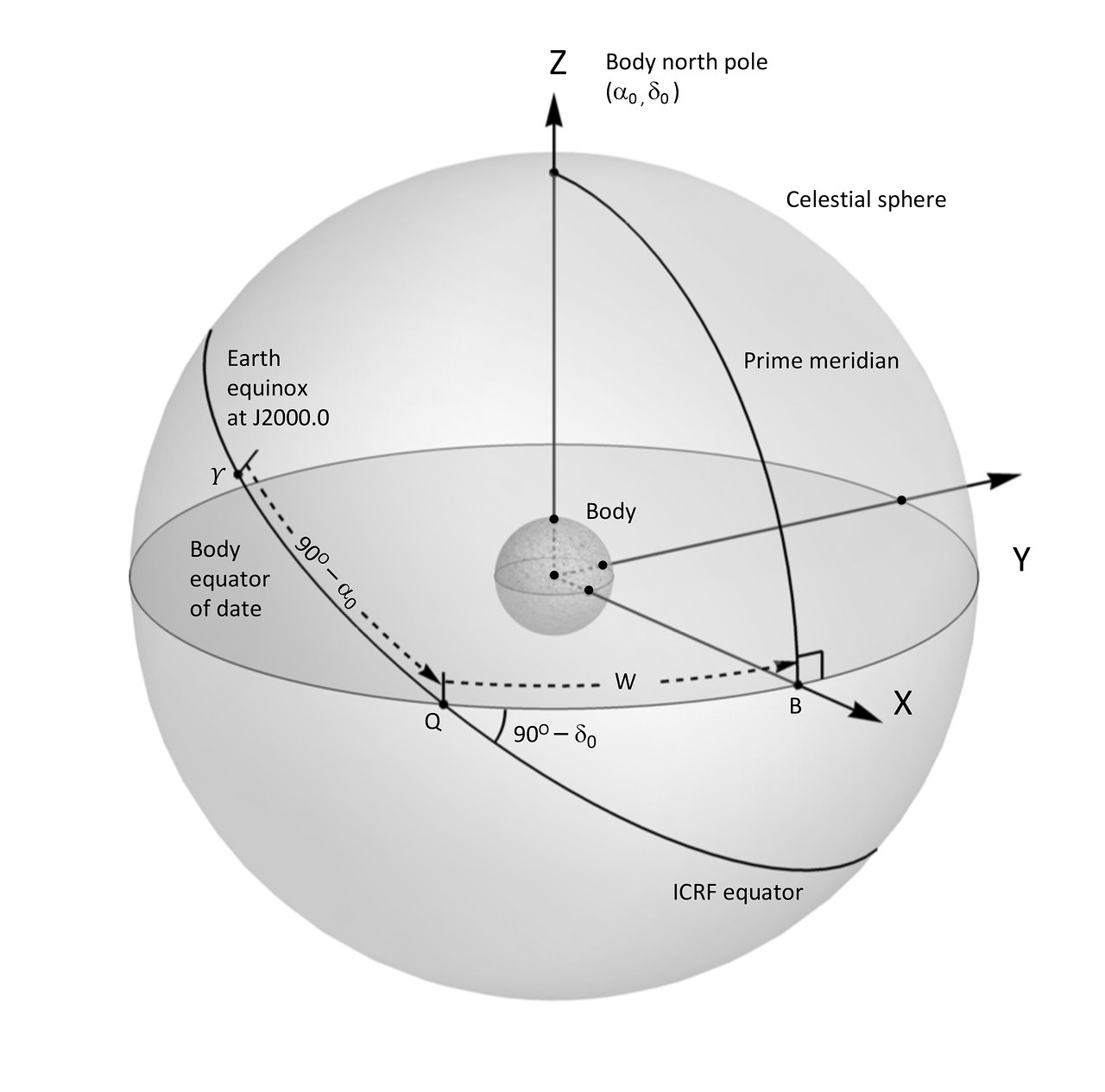
The IAU Working Group on Cartographic Coordinates and Rotational Elements (WGCCRE) is the keeper of official models that describe the cartographic coordinates and rotational elements of planetary bodies (such as the Earth, satellites, minor planets, and comets). Periodically, they release a report containing the coefficients to compute body orientations, based on the latest data available. These coefficients allow one to compute the rotation matrix from the ICRF frame to a body-fixed frame (for example, IAU Earth) by giving the direction of the pole vector and the prime meridian location as functions of time. An example Fortran module illustrating this for the IAU Earth frame is given below. The coefficients are taken from the 2009 IAU report [Reference 1]. Note that the IAU models are also available in SPICE (as "IAU_EARTH", "IAU_MOON", etc.). For Earth, the IAU model is not suitable for use in applications that require the highest possible accuracy (for that a more complex model would be necessary), but is quite acceptable for many applications.
module iau_orientation_module
use, intrinsic :: iso_fortran_env, only: wp => real64
implicit none
private
!constants:
real(wp),parameter :: zero = 0.0_wp
real(wp),parameter :: one = 1.0_wp
real(wp),parameter :: pi = acos(-one)
real(wp),parameter :: pi2 = pi/2.0_wp
real(wp),parameter :: deg2rad = pi/180.0_wp
real(wp),parameter :: sec2day = one/86400.0_wp
real(wp),parameter :: sec2century = one/3155760000.0_wp
public :: icrf_to_iau_earth
contains
!Rotation matrix from ICRF to IAU_EARTH
pure function icrf_to_iau_earth(et) result(rotmat)
implicit none
real(wp),intent(in) :: et !ephemeris time [sec from J2000]
real(wp),dimension(3,3) :: rotmat !rotation matrix
real(wp) :: w,dec,ra,d,t
real(wp),dimension(3,3) :: tmp
d = et * sec2day !days from J2000
t = et * sec2century !Julian centuries from J2000
ra = ( - 0.641_wp * t ) * deg2rad
dec = ( 90.0_wp - 0.557_wp * t ) * deg2rad
w = ( 190.147_wp + 360.9856235_wp * d ) * deg2rad
!it is a 3-1-3 rotation:
tmp = matmul( rotmat_x(pi2-dec), rotmat_z(pi2+ra) )
rotmat = matmul( rotmat_z(w), tmp )
end function icrf_to_iau_earth
!The 3x3 rotation matrix for a rotation about the x-axis.
pure function rotmat_x(angle) result(rotmat)
implicit none
real(wp),dimension(3,3) :: rotmat !rotation matrix
real(wp),intent(in) :: angle !angle [rad]
real(wp) :: c,s
c = cos(angle)
s = sin(angle)
rotmat = reshape([one, zero, zero, &
zero, c, -s, &
zero, s, c],[3,3])
end function rotmat_x
!The 3x3 rotation matrix for a rotation about the z-axis.
pure function rotmat_z(angle) result(rotmat)
implicit none
real(wp),dimension(3,3) :: rotmat !rotation matrix
real(wp),intent(in) :: angle !angle [rad]
real(wp) :: c,s
c = cos(angle)
s = sin(angle)
rotmat = reshape([ c, -s, zero, &
s, c, zero, &
zero, zero, one ],[3,3])
end function rotmat_z
end module iau_orientation_module
References
- B. A. Archinal, et al., "Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2009", Celest Mech Dyn Astr (2011) 109:101-135.
- J. Williams, Fortran Astrodynamics Toolkit - iau_orientation_module [GitHub]

The Standards of Fundamental Astronomy (SOFA) library is a very nice collection of routines that implement various IAU algorithms for fundamental astronomy computations. Versions are available in Fortran and C. Unfortunately, the Fortran version is written to be of maximum use to astronomers who frequently travel back in time to 1977 and compile the code on their UNIVAC (i.e., it is fixed-format Fortran 77). To assist 21st century users, I uploaded a little Python script called SofaMerge to Github. This script can make your life easier by merging all the individual source files into a single Fortran module file (with a few cosmetic updates along the way). It doesn't yet include any fixed to free format changes, but that could be easily added later.



