Degenerate Conic

GOTO Still Considered Harmful

For a number of years I have been familiar with the observation that the quality of programmers is a decreasing function of the density of go to statements in the programs they produce. -- Edsger W. Dijkstra

One of the classics of computer science is Edsger Dijkstra's "Go To Statement Considered Harmful", written in 1968. This missive argued that the GOTO statement (present in several languages at the time, including Fortran) was too primitive for high-level programming languages, and should be avoided.

Most people now agree with this, although some even today think that GOTOs are fine under some circumstances. They are present in C and C++, and are apparently used extensively in the Linux kernel. A recent study of C code in GitHub concluded that GOTO use is not that bad and is mainly used for error-handling and cleanup tasks, for situations where there are no better alternatives in C. However, C being a low-level language, we should not expect much from it. For modern Fortran users however, there are better ways to do these things. For example, unlike in C, breaking out of multiple loops is possible without GOTOs by using named DO loops with an EXIT statement like so:

a_loop : do a=1,n
    b_loop: do b=1,m
        !do some stuff ...
        if (done) exit a_loop ! break out of the outer loop
        !...
    end do b_loop
end do a_loop

In old-school Fortran (or C) this would be something like this:

do a=1,n
    do b=1,m
        ! do some stuff ...
        if (done) goto 10 ! break out of the outer loop
        ! ...
    end do
end do
10 continue

Of course, these two simple examples are both functionally equivalent, but the first one uses a much more structured approach. It's also a lot easier to follow what is going on. Once a line number is declared, there's nothing to stop a GOTO statement from anywhere in the code from jumping there (see spaghetti code). In my view, it's best to avoid this possibility entirely. In modern Fortran, DO loops (with CYCLE and EXIT), SELECT CASE statements, and other language constructs have obviated the need for GOTO for quite some time. Fortran 2008 added the BLOCK construct which was probably the final nail in the GOTO coffin, since it allows for the most common use cases (exception handing and cleanup) to be easily done without GOTOs. For example, in this code snippet, the main algorithm is contained within a BLOCK, and the exception handling code is outside:

main: block
    ! do some stuff ...
    if (error) exit main ! if there is a problem anywhere in this block,
    ! then exit to the exception handling code.
    ! ...
    return ! if everything is OK, then return
end block main

! exception handling code here

The cleanup case is similar (which is code that is always called):

main: block
    ! do some stuff ...
    if (need_to_cleanup) exit main ! for cleanup
    ! ...
end block main

! cleanup code here

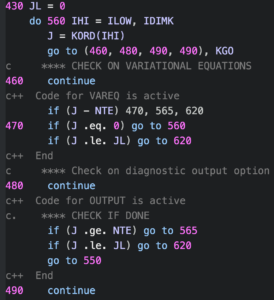
I don't believe any of the new programming languages that have cropped up in the past couple of decades has included a GOTO statement (although someone did create a goto statement for Python as an April Fool's joke in 2004). Of course, the presence of GOTO's doesn't mean the programmer is bad or that the code isn't going to work well. There is a ton of legacy Fortran 77 code out there that is rock solid, but unfortunately littered with GOTOs. An example is the DIVA integrator from the JPL MATH77 library (the screenshot above is from this code). First written in 1987, it is code of the highest quality, and has been used for decades in many spacecraft applications. However, it is also spaghetti code of the highest order, and seems like it would be unimaginably hard to maintain or modify at this point.

See also

• E. W. Dijkstra, "Go To Statement Considered Harmful", Communications of the ACM, Vol. 11, No. 3, March 1968, pp. 147-148 [online version here]
• E. A. Meyer, "Considered Harmful" Essays Considered Harmful, December 28, 2002.
• M. Nagappan, et. al, "An Empirical Study of Goto in C Code from GitHub Repositories", Proceedings of the 2015 10th Joint Meeting on Foundations of Software Engineering, Pages 404-414
• Using GOTO in Linux Kernel Code, January 13, 2003,

Fortran at 60

Today marks the 60th anniversary of the release of the original Fortran Programmer's Reference Manual. Fortran was the world's first high-level computer programming language, was developed beginning in 1953 at IBM by a team lead by John Backus. The first compiler was released in 1957. According to the manual, one of the main features was:

Object programs produced by FORTRAN will be nearly as efficient as those written by good programmers.

The first Fortran compiler (which was also the first optimizing compiler) was named one of the top 10 algorithms of the 20th century:

The creation of Fortran may rank as the single most important event in the history of computer programming: Finally, scientists (and others) could tell the computer what they wanted it to do, without having to descend into the netherworld of machine code. Although modest by modern compiler standards—Fortran I consisted of a mere 23,500 assembly-language instructions—the early compiler was nonetheless capable of surprisingly sophisticated computations. As Backus himself recalls in a recent history of Fortran I, II, and III, published in 1998 in the IEEE Annals of the History of Computing, the compiler "produced code of such efficiency that its output would startle the programmers who studied it."

The entire manual was only 51 pages long. Fortran has evolved significantly since the 1950s, and the descendant of this fairly simple language continues to be used today. The most recent version of the language (a 603 page ISO standard) was published in 2010.

See also

• John W. Backus, New York Times obituary, March 20, 2007.
• J. Backus, "The History of FORTRAN I, II, and III", ACM SIGPLAN Notices - Special issue: History of programming languages conference, Volume 13 Issue 8, August 1978, Pages 165 - 180.

Computing Pi

The digits of \(\pi\) can be computed using the "Spigot algorithm" [1-2]. The interesting thing about this algorithm is that it doesn't use any floating point computations, only integers.

A Fortran version of the algorithm is given below (a translation of the Pascal program in the reference). It computes the first 10,000 digits of \(\pi\). The nines and predigit business is because the algorithm will occasionally output 10 as the next digit, and the 1 will need to be added to the previous digit. If we know in advance that this won't occur for a given range of digits, then the code can be greatly simplified. It can also be reformulated to compute multiple digits at a time if we change the base (see [1] for the simplified version in base 10,000).

subroutine compute_pi()

    implicit none

    integer, parameter :: n = 10000 ! number of digits to compute
    integer, parameter :: len = 10*n/3 + 1

    integer :: i, j, k, q, x, nines, predigit
    integer, dimension(len) :: a

    a = 2
    nines = 0
    predigit = 0

    do j = 1, n
        q = 0
        do i = len, 1, -1
            x = 10*a(i) + q*i
            a(i) = mod(x, 2*i - 1)
            q = x/(2*i - 1)
        end do
        a(1) = mod(q, 10)
        q = q/10
        if (q == 9) then
            nines = nines + 1
        else if (q == 10) then
            write (*, '(I1)', advance='NO') predigit + 1
            do k = 1, nines
                write (*, '(I1)', advance='NO') 0
            end do
            predigit = 0
            nines = 0
        else
            if (j == 2) then
                write (*, '(I1,".")', advance='NO') predigit
            else if (j /= 1) then
                write (*, '(I1)', advance='NO') predigit
            end if
            predigit = q
            if (nines /= 0) then
            do k = 1, nines
                write (*, '(I1)', advance='NO') 9
            end do
            nines = 0
            end if
        end if
    end do
    write (*, '(I1)', advance='NO') predigit

end subroutine compute_pi

The algorithm as originally published contained a mistake (len = 10*n/3). The correction is due to [3]. The code above produces the following output:

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132000568127145263560827785771342757789609173637178721468440901224953430146549585371050792279689258923542019956112129021960864034418159813629774771309960518707211349999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420198938095257201065485863278865936153381827968230301952035301852968995773622599413891249721775283479131515574857242454150695950829533116861727855889075098381754637464939319255060400927701671139009848824012858361603563707660104710181942955596198946767837449448255379774726847104047534646208046684259069491293313677028989152104752162056966024058038150193511253382430035587640247496473263914199272604269922796782354781636009341721641219924586315030286182974555706749838505494588586926995690927210797509302955321165344987202755960236480665499119881834797753566369807426542527862551818417574672890977772793800081647060016145249192173217214772350141441973568548161361157352552133475741849468438523323907394143334547762416862518983569485562099219222184272550254256887671790494601653466804988627232791786085784383827967976681454100953883786360950680064225125205117392984896084128488626945604241965285022210661186306744278622039194945047123713786960956364371917287467764657573962413890865832645995813390478027590099465764078951269468398352595709825822620522489407726719478268482601476990902640136394437455305068203496252451749399651431429809190659250937221696461515709858387410597885959772975498930161753928468138268683868942774155991855925245953959431049972524680845987273644695848653836736222626099124608051243884390451244136549762780797715691435997700129616089441694868555848406353422072225828488648158456028506016842739452267467678895252138522549954666727823986456596116354886230577456498035593634568174324112515076069479451096596094025228879710893145669136867228748940560101503308617928680920874760917824938589009714909675985261365549781893129784821682998948722658804857564014270477555132379641451523746234364542858444795265867821051141354735739523113427166102135969536231442952484937187110145765403590279934403742007310578539062198387447808478489683321445713868751943506430218453191048481005370614680674919278191197939952061419663428754440643745123718192179998391015919561814675142691239748940907186494231961567945208095146550225231603881930142093762137855956638937787083039069792077346722182562599661501421503068038447734549202605414665925201497442850732518666002132434088190710486331734649651453905796268561005508106658796998163574736384052571459102897064140110971206280439039759515677157700420337869936007230558763176359421873125147120532928191826186125867321579198414848829164470609575270695722091756711672291098169091528017350671274858322287183520935396572512108357915136988209144421006751033467110314126711136990865851639831501970165151168517143765761835155650884909989859982387345528331635507647918535893226185489632132933089857064204675259070915481416549859461637180270981994309924488957571282890592323326097299712084433573265489382391193259746366730583604142813883032038249037589852437441702913276561809377344403070746921120191302033038019762110110044929321516084244485963766983895228684783123552658213144957685726243344189303968642624341077322697802807318915441101044682325271620105265227211166039666557309254711055785376346682065310989652691862056476931257058635662018558100729360659876486117910453348850346113657686753249441668039626579787718556084552965412665408530614344431858676975145661406800700237877659134401712749470420562230538994561314071127000407854733269939081454664645880797270826683063432858785698305235808933065757406795457163775254202114955761581400250126228594130216471550979259230990796547376125517656751357517829666454779174501129961489030463994713296210734043751895735961458901938971311179042978285647503203198691514028708085990480109412147221317947647772622414254854540332157185306142288137585043063321751829798662237172159160771669254748738986654949450114654062843366393790039769265672146385306736096571209180763832716641627488880078692560290228472104031721186082041900042296617119637792133757511495950156604963186294726547364252308177036751590673502350728354056704038674351362222477158915049530984448933309634087807693259939780541934144737744184263129860809988868741326047215695162396586457302163159819319516735381297416772947867242292465436680098067692823828068996400482435403701416314965897940924323789690706977942236250822168895738379862300159377647165122893578601588161755782973523344604281512627203734314653197777416031990665541876397929334419521541341899485444734567383162499341913181480927777103863877343177207545654532207770921201905166096280490926360197598828161332316663652861932668633606273567630354477628035045077723554710585954870279081435624014517180624643626794561275318134078330336254232783944975382437205835311477119926063813346776879695970309833913077109870408591337464144282277263465947047458784778720192771528073176790770715721344473060570073349243693113835049316312840425121925651798069411352801314701304781643788518529092854520116583934196562134914341595625865865570552690496520985803385072242648293972858478316305777756068887644624824685792603953527734803048029005876075825104747091643961362676044925627420420832085661190625454337213153595845068772460290161876679524061634252257719542916299193064553779914037340432875262888963995879475729174642635745525407909145135711136941091193932519107602082520261879853188770584297259167781314969900901921169717372784768472686084900337702424291651300500516832336435038951702989392233451722013812806965011784408745196012122859937162313017114448464090389064495444006198690754851602632750529834918740786680881833851022833450850486082503930213321971551843063545500766828294930413776552793975175461395398468339363830474611996653858153842056853386218672523340283087112328278921250771262946322956398989893582116745627010218356462201349671518819097303811980049734072396103685406643193950979019069963955245300545058068550195673022921913933918568034490398205955100226353536192041994745538593810234395544959778377902374216172711172364343543947822181852862408514006660443325888569867054315470696574745855033232334210730154594051655379068662733379958511562578432298827372319898757141595781119635833005940873068121602876496286744604774649159950549737425626901049037781986835938146574126804925648798556145372347867330390468838343634655379498641927056387293174872332083760112302991136793862708943879936201629515413371424892830722012690147546684765357616477379467520049075715552781965362132392640616013635815590742202020318727760527721900556148425551879253034351398442532234157623361064250639049750086562710953591946589751413103482276930624743536325691607815478181152843667957061108615331504452127473924544945423682886061340841486377670096120715124914043027253860764823634143346235189757664521641376796903149501910857598442391986291642193994907236234646844117394032659184044378051333894525742399508296591228508555821572503107125701266830240292952522011872676756220415420516184163484756516999811614101002996078386909291603028840026910414079288621507842451670908700069928212066041837180653556725253256753286129104248776182582976515795984703562226293486003415872298053498965022629174878820273420922224533985626476691490556284250391275771028402799806636582548892648802545661017296702664076559042909945681506526530537182941270336931378517860904070866711496558343434769338578171138645587367812301458768712660348913909562009939361031029161615288138437909904231747336394804575931493140529763475748119356709110137751721008031559024853090669203767192203322909433467685142214477379393751703443661991040337511173547191855046449026365512816228824462575916333039107225383742182140883508657391771509682887478265699599574490661758344137522397096834080053559849175417381883999446974867626551658276584835884531427756879002909517028352971634456212964043523117600665101241200659755851276178583829204197484423608007193045761893234922927965019875187212726750798125547095890455635792122103334669749923563025494780249011419521238281530911407907386025152274299581807247162591668545133312394804947079119153267343028244186041426363954800044800267049624820179289647669758318327131425170296923488962766844032326092752496035799646925650493681836090032380929345958897069536534940603402166544375589004563288225054525564056448246515187547119621844396582533754388569094113031509526179378002974120766514793942590298969594699556576121865619673378623625612521632086286922210327488921865436480229678070576561514463204692790682120738837781423356282360896320806822246801224826117718589638140918390367367222088832151375560037279839400415297002878307667094447456013455641725437090697939612257142989467154357846878861444581231459357198492252847160504922124247014121478057345510500801908699603302763478708108175450119307141223390866393833952942578690507643100638351983438934159613185434754649556978103829309716465143840700707360411237359984345225161050702705623526601276484830840761183013052793205427462865403603674532865105706587488225698157936789766974220575059683440869735020141020672358502007245225632651341055924019027421624843914035998953539459094407046912091409387001264560016237428802109276457931065792295524988727584610126483699989225695968815920560010165525637567

See also

1. S. Rabinowitz, Abstract 863–11–482: A Spigot Algorithm for Pi, American Mathematical Society, 12(1991)30, 1991.
2. S. Rabinowitz, S. Wagon, "A Spigot Algorithm for the Digits of \(\pi\)", American Mathematical Monthly, Vol. 102, Issue 3, March 1995, p. 195-203.
3. J. Arndt, C. Haenel, π Unleashed, Springer, 2000.

Backward Compatibility

"Perfection is achieved, not when there is nothing more to add, but when there is nothing left to take away." -- Antoine de Saint-Exupéry

The Fortran standards committee generally refuses to break backward compatibility when Fortran is updated. This is a good thing (take that, Python), and code written decades ago can still be compiled fine today. However, over the years, various old features of the language have been identified as "obsolescent", namely:

• Alternate return
• Assumed-length character functions
• CHARACTER*(*) form of CHARACTER declaration
• Computed GO TO statement
• DATA statements among executable statements
• Fixed source form
• Statement functions
• ENTRY statement
• Labeled DO loops [will be obsolescent in Fortran 2015]
• EQUIVALENCE [will be obsolescent in Fortran 2015]
• COMMON Blocks [will be obsolescent in Fortran 2015]
• BLOCK DATA [will be obsolescent in Fortran 2015]

And a small set of features has actually been deleted from the language standard:

• ASSIGN and assigned GO TO statements
• Assigned FORMAT specifier
• Branching to an END IF statement from outside its IF block
• H edit descriptor
• PAUSE statement
• Real and double precision DO control variables and DO loop control expressions
• Arithmetic IF [will be deleted in Fortran 2015]
• Shared DO termination and termination on a statement other than END DO or CONTINUE [will be deleted in Fortran 2015]

In practice, all compilers still support all the old features (although special compiler flags may be necessary to use them). Normally, you shouldn't use any of this junk in new code. But there is still a lot of legacy FORTRAN 77 code out there that people want (or need) to compile. However, as I've shown many times in this blog, updating old Fortran code to modern standards is not really that big of a deal.

When the next revision of the language (Fortran 2015) is published, it will mark the first time since Fortran was first standardized in 1966 that we will have two consecutive minor revisions of the language (2008 was also a minor revision). The last major revision of the language was Fortran 2003 over a decade ago. There still is no feature-complete free Fortran 2003 compiler (although gfortran currently does include almost all of the Fortran 2003 standard).

Personally, I would tend to prefer a faster-paced cycle of Fortran language development. I'm not one of those who think the language should include regular expressions or a 2D graphics API (seriously, C++?). But, there are clearly potentially useful things that are missing. I think the standard should finally acknowledge the existence of the file system, and provide intrinsic routines for changing and creating directories, searching for files, etc. Currently, if you want to do anything like that you have to resort to system calls or non-standard extensions provided by your compiler vender (thus making the code less portable). A much more significant upgrade would be better support for generic programming (maybe we'll get that in Fortran 2025). There are also many other feature proposals out there (see references below).

See also

• Fortran Feature Proposals – at the Fortran Wiki.
• E. Myklebust, Feature Proposals for Fortran – The Complete Set, ISO/IEC JTC1/SC22/WG5 N1972
• C. Page, "Suggestion: Improved String-handling in Fortran", October 1, 2015.
• V. Snyder, "Units of Measure in Fortran", N1970, April 22, 2013.
• S. Lionel, "The Future of Fortran", March 27, 2015

Syntax Highlighting

Decently syntax highlighted Fortran code on the internet is hard to come by. None of the major sites where people are likely to visit to learn about Fortran have it:

• The Google Groups hosting of comp.lang.fortran (I don't really expect much from this one since it's just Usenet.)
• Stack Overflow (we should expect better from them, since they have had syntax highlighting for many other languages for years.) It looks like they are using Google's code-prettify (which seems to have a pull request ready to provide syntax highlighting for Fortran, so perhaps there is hope?)
• Intel Fortran compiler documentation [example] (people pay good money for this compiler, and so should ask for better documentation).
• GFortran documentation (their entire Fortran website looks like it is from the late 1990s, and could certainly use an overhaul).

Luckily GitHub has syntax highlighting for Fortran, as well as the Fortran Wiki.

Personally, I hate looking at non-syntax highlighted code. It's not aesthetically pleasing and I find it hard to read. On this blog, I'm using a Fortran plugin for SyntaxHighlighter Evolved, which I downloaded somewhere at some point and have modified to account for various newer Fortran language features. It's not perfect, but it looks pretty good.

Consider this example from the gfortran website:

Now that looks just awful, and not just because they are using ancient syntax such as (/, /), and .eq.. Whereas the following syntax-highlighted one looks great:

program test_all

implicit none

logical :: l

l = all([.true., .true., .true.])
write(*,*) l
call section()

contains

subroutine section()

integer,dimension(2,3) :: a, b

a = 1
b = 1
b(2,2) = 2
write(*,*) all(a == b, 1)
write(*,*) all(a == b, 2)

end subroutine section

end program test_all

FORD-produced documentation has nice syntax highlighting for Fortran code provided by Pygments (which is written in Python). An example can be found here. Rouge is another code highlighter (written in Ruby) that supports Fortran and can output as HTML. Both Pygments and Rouge are open source and released under permissive licenses.

Intel Fortran Compiler 17.0

Intel has announced the availability of version 17.0 of the Intel Fortran Compiler (part of Intel Parallel Studio XE 2017). Slowly but surely, the compiler is approaching full support for the current Fortran 2008 standard. New Fortran 2008 features added in this release are:

• TYPE(intrinsic-type)
• Pointer initialization
• Implied-shape PARAMETER arrays
• Extend EXIT statement to all valid construct names
• Support BIND(C) in internal procedures

In addition, the compiler now also supports the standard auto-reallocation on assignment by default (previously, you had to use a special compiler flag to enable this behavior).

See also

• Intel Fortran Compiler 17.0 Release Notes
• J. Reid, The new features of Fortran 2008, ISO/IEC JTC1/SC22/WG5 N1729, May 27, 2008

JSON-Fortran 5.1

JSON-Fortran 5.1 is out. There are several new features in this release. I added a get_path() routine that can be used to return the path of a variable in a JSON structure. This can be used along with the traverse() routine to do something pseudointeresting: convert a JSON file into a Fortran namelist file. Why would anyone want to do that, you ask? Who knows. Consider the following example:

program why

    use json_module

    implicit none

    type(json_core) :: json
    type(json_value), pointer :: p
    integer :: iunit !! file unit

    open (newunit=iunit, file='data.nml', status='REPLACE')
    write (iunit, '(A)') '&DATA'
    call json%initialize()
    call json%parse(file='data.json', p=p)
    call json%traverse(p, print_json_variable)
    write (iunit, '(A)') '/'
    close (iunit)

contains

    subroutine print_json_variable(json, p, finished)

        !! A `traverse` routine for printing out all
        !! the variables in a JSON structure.

        implicit none

        class(json_core), intent(inout) :: json
        type(json_value), pointer, intent(in) :: p
        logical(json_LK), intent(out) :: finished

        character(kind=json_CK, len=:), allocatable :: path
        character(kind=json_CK, len=:), allocatable :: value
        logical(json_LK) :: found
        type(json_value), pointer :: child
        integer(json_IK) :: var_type

        call json%get_child(p, child)
        finished = .false.

        !only print the leafs:
        if (.not. associated(child)) then
            !fortran-style:
            call json%get_path(p, path, found, &
                               use_alt_array_tokens=.true., &
                               path_sep=json_CK_'%')
            if (found) then
                call json%info(p, var_type=var_type)
                select case (var_type)
                case (json_array, json_object)
                    !an empty array or object
                    !don't print anything
                    return
                case (json_string)
                    ! note: strings are returned escaped
                    ! without quotes
                    call json%get(p, value)
                    value = '"'//value//'"'
                case default
                    ! get the value as a string
                    ! [assumes strict_type_checking=false]
                    call json%get(p, value)
                end select
                !check for errors:
                if (json%failed()) then
                    finished = .true.
                else
                    write (iunit, '(A)') &
                        path//json_CK_' = '//value//','
                end if
            else
                finished = .true.
            end if
        end if

    end subroutine print_json_variable

end program why

Here, we are simply traversing the entire JSON structure, and printing out the paths of the leaf nodes using a namelist-style syntax. For the example JSON file:

{
    "t": 0.0,
    "x": [1.0, 2.0, 3.0],
    "m": 2000.0,
    "name": "foo"
}

This program will produce the following namelist file:

&DATA
t = 0.0E+0,
x(1) = 0.1E+1,
x(2) = 0.2E+1,
x(3) = 0.3E+1,
m = 0.2E+4,
name = "foo",
/

Which could be read using the following Fortran program:

program namelist_test

use iso_fortran_env, only: wp => real64

implicit none

real(wp) :: t,m,x(3)
integer :: iunit,istat
character(len=10) :: name

! define the namelist:
namelist /DATA/ t,x,m,name

! read the namelist:
open(newunit=iunit,file='data.nml',status='OLD')
read(unit=iunit,nml=DATA,iostat=istat)
close(unit=iunit)

end program namelist_test

There is also a new minification option for printing a JSON structure with no extra whitespace. For example:

{"t":0.0E+0,"x":[0.1E+1,0.2E+1,0.3E+1],"m":0.2E+4,"name":"foo"}

See also

• f90nml -- A Python module for parsing Fortran namelist files

Dynamically Sizing Arrays

Often the need arises to add (or subtract) elements from an array on the fly. Fortran 2008 allows for this to be easily done using standard allocatable arrays. An example for integer arrays is shown here:

integer,dimension(:),allocatable :: x

x = [1,2,3]
x = [x,[4,5,6]] ! x is now [1,2,3,4,5,6]
x = x(1:4) ! x is now [1,2,3,4]

Note that, if using the Intel compiler, this behavior is not enabled by default for computational efficiency reasons. To enable it you have to use the -assume realloc_lhs compiler flag.

Resizing an array like this carries a performance penalty. When adding a new element, the compiler will likely have to make a temporary copy of the array, deallocate the original and resize it, and then copy over the original elements and the new one. A simple test case is shown here (compiled with gfortran 6.1.0 with -O3 optimization enabled):

program test

implicit none

integer,dimension(:),allocatable :: x
integer :: i

x = [0]
do i=1,100000
    x = [x,i]
end do

end program test

This requires 2.828986 seconds on my laptop (or 35,348 assignments per second). Now, that may be good enough for some applications. However, performance can be improved significantly by allocating the array in chunks, as shown in the following example, where we allocate in chunks of 100 elements, and then resize it to the correct size at the end:

program test

    implicit none

    integer, dimension(:), allocatable :: x
    integer :: i, n

    integer, parameter :: chunk_size = 100

    n = 0
    do i = 0, 100000
        call add_to(x, i, n, chunk_size, finished=i == 100000)
    end do

contains

    pure subroutine add_to(vec, val, n, chunk_size, finished)

        implicit none

        integer, dimension(:), allocatable, intent(inout) :: vec
            !! the vector to add to
        integer, intent(in) :: val
            !! the value to add
        integer, intent(inout) :: n
            !! counter for last element added to vec.
            !! must be initialized to size(vec)
            !! (or 0 if not allocated) before first call
        integer, intent(in) :: chunk_size
            !! allocate vec in blocks of this size (>0)
        logical, intent(in) :: finished
            !! set to true to return vec
            !! as its correct size (n)

        integer, dimension(:), allocatable :: tmp

        if (allocated(vec)) then
            if (n == size(vec)) then
                ! have to add another chunk:
                allocate (tmp(size(vec) + chunk_size))
                tmp(1:size(vec)) = vec
                call move_alloc(tmp, vec)
            end if
            n = n + 1
        else
            ! the first element:
            allocate (vec(chunk_size))
            n = 1
        end if

        vec(n) = val

        if (finished) then
            ! set vec to actual size (n):
            if (allocated(tmp)) deallocate (tmp)
            allocate (tmp(n))
            tmp = vec(1:n)
            call move_alloc(tmp, vec)
        end if

    end subroutine add_to

end program test

This requires only 0.022938 seconds (or 4,359,577 assignments per second) which is nearly 123 times faster. Note that we are using the Fortran 2003 move_alloc intrinsic function, which saves us an extra copy operation when the array is resized.

Increasing the chunk size can improve performance even more:

Depending on the specific application, a linked list is another option for dynamically-sized objects.

Natural Sorting

Sorting is one of the fundamental problems in computer science, so of course Fortran does not include any intrinsic sorting routine (we've got Bessel functions, though!) String sorting is a special case of this problem which includes various choices to consider, for example:

• Natural or ASCII sorting
• Case sensitive (e.g., 'A'<'a') or case insensitive (e.g., 'A'=='a')

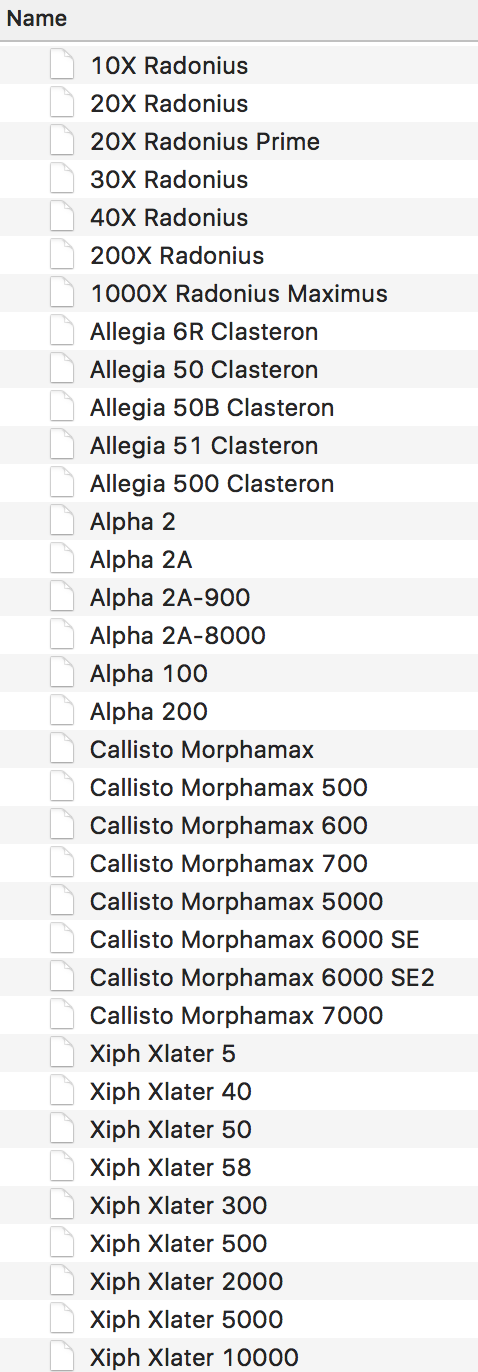
"Natural" sorting (also called "alphanumeric sorting" means to take into account numeric values in the string, rather than just comparing the ASCII value of each of the characters. This can produce an order that looks more natural to a human for strings that contain numbers. For example, in a "natural" sort, the string "case2.txt" will come before "case100.txt", since the number 2 comes before the number 100. For example, natural sorting is the method used to sort file names in the MacOS X Finder (see image at right). While, interestingly, an ls -l from a Terminal merely does a basic ASCII sort.

For string sorting routines written in modern Fortran, check out my GitHub project stringsort. This library contains routines for both natural and ASCII string sorting. Natural sorting is achieved by breaking up each string into chunks. A chunk consists of a non-numeric character or a contiguous block of integer characters. A case insensitive search is done by simply converting each character to lowercase before comparing them. I make no claim that the routines are particularly optimized. One limitation is that contiguous integer characters are stored as an integer(INT32) value, which has a maximum value of 2147483647. Although note that it is easy to change the code to use integer(INT64) variables to increase this range up to 9223372036854775807 if necessary. Eliminating integer size restrictions entirely is left as an exercise for the reader.

Consider the following test case:

character(len=*),dimension(6) :: &
str = [ 'z1.txt ', &
        'z102.txt', &
        'Z101.txt', &
        'z100.txt', &
        'z10.txt ', &
        'Z11.txt ' ]

This list can be sorted (at least) four different ways:

Case Insensitive

ASCII

z1.txt z10.txt z100.txt Z101.txt z102.txt Z11.txt

natural

z1.txt z10.txt Z11.txt z100.txt Z101.txt z102.txt

Case Sensitive

ASCII

Z101.txt Z11.txt z1.txt z10.txt z100.txt z102.txt

natural

Z11.txt Z101.txt z1.txt z10.txt z100.txt z102.txt

Each of these can be done using stringsort with the following subroutine calls:

call lexical_sort_recursive(str,case_sensitive=.false.)
call lexical_sort_natural_recursive(str,case_sensitive=.false.)

call lexical_sort_recursive(str,case_sensitive=.true.)
call lexical_sort_natural_recursive(str,case_sensitive=.true.)

The routines use the quicksort algorithm, which was originally created for sorting strings (specifically words in Russian sentences so they could be looked up in a Russian-English dictionary). The algorithm is easily implemented in modern Fortran using recursion (non-recursive versions were also available before recursion was added to the language in Fortran 90). Quicksort was named one of the top 10 algorithms of the 20th century by the ACM (Fortran was also on the list).

See also

• David Koelle, The Alphanum Algorithm
• C. A. R. Hoare, Algorithm 64: Quicksort, Communications of the ACM, Volume 4 Issue 7, July 1961

Distant Retrograde Orbits

A "distant-retrograde orbit" (DRO) is a periodic orbit in the circular restricted three-body problem (CR3BP) that, in the rotating frame, looks like a large quasi-elliptical retrograde orbit around the secondary body. Moon-centered DRO's in the Earth-Moon system were considered as a possible destination for depositing a captured asteroid for NASA's proposed Asteroid Redirect Mission, since they can remain stable for long periods of time (decades or even centuries).

DROs can be computed using components from the Fortran Astrodynamics Toolkit. All we need is:

• A numerical integrator (we will use an 8th order Runge-Kutta method from Shanks [4]).
• The equations of motion for the circular restricted three-body problem (CR3BP).
• A nonlinear equation solver (we will use HYBRD1 from MINPACK).

We will use the canonical normalized CR3BP reference frame where the distance between the primary and secondary body is normalized to one. The initial state is placed on the x-axis, at a specified distance from the Moon. The y-velocity \(v_y\) is allowed to vary, and \(v_x=0\). The problem can be solved with two optimization variables:

1. The time of flight for one orbit period (i.e., the duration between two consecutive x-axis crossings on the \(x>1\) side)
2. The initial y-velocity component

and two constraints:

1. \(y=0\) at the final time
2. \(v_x=0\) at the final time (i.e., a perpendicular crossing of the x-axis)

The problem can be simplified to one variable and one constraint by using an integrator with an event-finding capability so that the integration proceeds until the x-axis crossing occurs (eliminating the time of flight and the \(y=0\) constraint from the optimization problem). That is how we will proceed here, since the Runge-Kutta module we are using does include an event location capability.

The code for computing a single Earth-Moon DRO is shown here:

program dro_test

    use fortran_astrodynamics_toolkit

    implicit none

    real(wp), parameter :: mu_earth = 398600.436233_wp
        !! km^3/s^2
    real(wp), parameter :: mu_moon = 4902.800076_wp
        !! km^3/s^2
    integer, parameter :: n = 6
        !! number of state variables
    real(wp), parameter :: t0 = 0.0_wp
        !! initial time (normalized)
    real(wp), parameter :: tmax = 1000.0_wp
        !! max final time (normalized)
    real(wp), parameter :: dt = 0.001_wp
        !! time step (normalized)
    real(wp), parameter :: xtol = 1.0e-4_wp
        !! tolerance for hybrd1
    integer, parameter :: maxfev = 1000
        !! max number of function evaluations for hybrd1
    real(wp), dimension(n), parameter :: x0 = &
                                         [1.2_wp, &
                                          0.0_wp, &
                                          0.0_wp, &
                                          0.0_wp, &
                                          -0.7_wp, &
                                          0.0_wp]
    !! initial guess for DRO state (normalized)

    real(wp), dimension(1) :: vy0
        !! initial y velocity (xvec for hybrd1)
    real(wp), dimension(1) :: vxf
        !! final x velocity (fvec for hybrd1)
    real(wp) :: mu
        !! CRTPB parameter
    type(rk8_10_class) :: prop
        !! integrator
    integer :: info
        !! hybrd1 status flag

    ! compute the CRTBP parameter & Jacobi constant:
    mu = compute_crtpb_parameter(mu_earth, mu_moon)

    ! initialize integrator:
    call prop%initialize(n, func, g=x_axis_crossing)

    ! now, solve for DRO:
    vy0 = x0(5) ! initial guess
    call hybrd1(dro_fcn, 1, vy0, vxf, tol=xtol, info=info)

    ! solution:
    write (*, *) ' info=', info
    write (*, *) ' vy0=', vy0
    write (*, *) ' vxf=', vxf

contains

!**************************************

    subroutine dro_fcn(n, xvec, fvec, iflag)
        !! DRO function for hybrd1

        implicit none

        integer, intent(in) :: n !! `n=1` in this case
        real(wp), dimension(n), intent(in) :: xvec !! `vy0`
        real(wp), dimension(n), intent(out) :: fvec !! `vxf`
        integer, intent(inout) :: iflag !! not used here

        real(wp) :: gf, t0, tf_actual
        real(wp), dimension(6) :: x, xf

        real(wp), parameter :: tol = 1.0e-8_wp
            !! event finding tolerance

        t0 = zero ! epoch doesn't matter for crtbp
        x = x0 ! initial guess state
        x(5) = xvec(1) ! vy0 (only optimization variable)

        !integrate to the next x-axis crossing:
        call prop%integrate_to_event(t0, x, dt, tmax, tol, tf_actual, xf, gf)

        !want x-velocity at the x-axis crossing to be zero:
        fvec = xf(4)

    end subroutine dro_fcn

!**************************************

    subroutine func(me, t, x, xdot)
        !! CRTBP derivative function

        implicit none

        class(rk_class), intent(inout) :: me
        real(wp), intent(in) :: t
        real(wp), dimension(me%n), intent(in) :: x
        real(wp), dimension(me%n), intent(out) :: xdot

        call crtbp_derivs(mu, x, xdot)

    end subroutine func

!**************************************

    subroutine x_axis_crossing(me, t, x, g)
        !! x-axis crossing event function

        implicit none

        class(rk_class), intent(inout) :: me
        real(wp), intent(in) :: t
        real(wp), dimension(me%n), intent(in) :: x
        real(wp), intent(out) :: g

        g = x(2) ! y = 0 at x-axis crossing

    end subroutine x_axis_crossing

end program dro_test

Trajectory plots for some example solutions are shown below (each with a different x component). The L1 and L2 libration points are also shown. In this plot, the Earth is at the origin and the Moon is at [x=1,y=0]. See this example for more details.

References

1. The Restricted Three-Body Problem - MIT OpenCourseWare, S. Widnall 16.07 Dynamics Fall 2008, Version 1.0.
2. C. A. Ocampo, G. W. Rosborough, "Transfer trajectories for distant retrograde orbiters of the Earth", AIAA Spaceflight Mechanics Meeting, Pasadena, CA, Feb. 22-24, 1993.
3. Asteroid Redirect Mission and Human Space Flight, June 19, 2013.
4. E. B. Shanks, "Higher Order Approximations of Runge-Kutta Type", NASA Technical Note, NASA TN D-2920, Sept. 1965.
5. Henon, M., "Numerical Exploration of the Restricted Problem. V. Hill's Case: Periodic Orbits and Their Stability," Astronomy and Astrophys. Vol 1, 223-238, 1969.