Degenerate Conic

Old School

I came across this old NASA document from 1963, where a cross product subroutine is defined in Fortran (based on some of the other routines given, it looks like they were using FORTRAN II):

A cross product function is always a necessary procedure in any orbital mechanics simulation (for example when computing the angular momentum vector \(\mathbf{h} = \mathbf{r} \times \mathbf{v}\)). The interesting thing is that this subroutine will still compile today with any Fortran compiler. Of course, there are a few features used here that are deemed obsolescent in modern Fortran (fixed-form source, implicit typing, and the DIMENSION statement). Also it is using single precision reals (which no one uses anymore in this field). A modernized version would look something like this:

subroutine cross(a,b,c)
implicit none
real(wp),dimension(3),intent(in) :: a,b
real(wp),dimension(3),intent(out) :: c
c(1) = a(2)*b(3)-a(3)*b(2)
c(2) = a(3)*b(1)-a(1)*b(3)
c(3) = a(1)*b(2)-a(2)*b(1)
end subroutine cross

But, basically, except for declaring the real kind, it does exactly the same thing as the one from 1963. The modern routine would presumably be put in a module (in which the WP kind parameter is accessible), for example, a vector utilities module. While a subroutine is perfectly acceptable for this case, my preference would be to use a function like so:

pure function cross(a,b) result(c)
implicit none
real(wp),dimension(3),intent(in) :: a,b
real(wp),dimension(3) :: c
c(1) = a(2)*b(3)-a(3)*b(2)
c(2) = a(3)*b(1)-a(1)*b(3)
c(3) = a(1)*b(2)-a(2)*b(1)
end function cross

This one is a function that return a \(\mathrm{3} \times \mathrm{1}\) vector, and is explicitly declared to be PURE (which can allow for more aggressive code optimizations from the compiler).

This document, which is the programmer's manual for an interplanetary error propagation program, contains a lot of other Fortran gems. It also has some awesome old school flow charts:

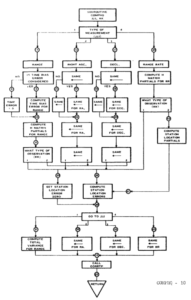
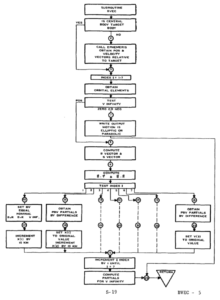
See also

• Programmer's Manual for Interplanetary Error Propagation Program, Philco Corp., NASA-CR-69535, Nov 15, 1963

Orbital Mechanics with Fortran

Many of NASA's workhorse spacecraft trajectory optimization tools are written in Fortran or have Fortran components (e.g., OTIS, MALTO, Mystic, and Copernicus). None of it is really publicly-available however. There are some freely-available Fortran codes around for general-purpose orbital mechanics applications. Including:

• Fortran Astrodynamics Toolkit — A Modern Fortran Library for Astrodynamics. This is my hobby library that is coming along nicely, and includes a lot of different algorithms. See also my other GitHub projects for other components that are useful in the orbital mechanics field (such as integrators and optimizers). All of it is open source with a permissive BSD license (so you can use it for whatever you want).
• Low-Level Engine for Astrodynamics (LLEA) another modern Fortran astrodynamics library on GitHub
• Astrodynamics Software from Fundamentals of Astrodynamics and Applications by David Vallado
• Orbital Mechanics with Fortran by Dave Eagle
• IAU Standards of Fundamental Astronomy (SOFA)
• Naval Observatory Vector Astrometry Software (NOVAS)
• SPICE Toolkit from JPL/NAIF for solar system geometry
• Swifter — an improved solar system integration software package

You can also find some old Fortran gems in various papers on the NASA Technical Reports Server.

See also

1. J. Williams, R. D. Falck, and I. B. Beekman. "Application of Modern Fortran to Spacecraft Trajectory Design and Optimization", 2018 Space Flight Mechanics Meeting, AIAA SciTech Forum, (AIAA 2018-1451)

Another One Bites the Dust: GRAM Atmosphere Model

It looks like the Fortran community has lost another venerable NASA Fortran library to C++. I recently noticed that the latest release of NASA's Global Reference Atmosphere Model (GRAM) is now C++. From the release link:

Earth-GRAM 2016 is now available as an open-source C++ computer code that can run on a variety of platforms including PCs and UNIX stations. The software provides a model that offers values for atmospheric parameters such as density, temperature, winds, and constituents for any month and at any altitude and location within the Earth's atmosphere. Earth-GRAM 2010 is available in FORTRAN. Similar computer models of Mars, Venus, Titan, and Neptune are available for diverse mission applications through NASA’s Space Environments and Effects (SEE) Program, a partnership with industry, academia, and other government agencies that seeks to develop more reliable, more effective spacecraft.

The Earth-GRAM model, originally written in Fortran 77, is produced by MSFC and has been around for a while, with many revisions (i.e., GRAM-86, GRAM-88, GRAM-90, GRAM-95, GRAM-99, GRAM 2007, and GRAM 2010). In the 2010 revision, they converted the old Fortran 77 code to Fortran 90, which I thought was a step in the right direction (although maybe 20 years too late). It seems like they could have used Fortran 2003 and provided a C interface using the standard Fortran/C Interoperability feature, which would have enabled calling it from a variety of languages (including C++).

I remain utterly unconvinced that C++ is the programming language that engineers and scientists should be using. Are CS people taking over programming jobs once done by engineers? Is this a failure of university engineering departments? Although it seems like even CS people don't want to be using C++ anymore. Every time I turn around a new programming language (Java, Rust, Go, D, C#, Swift, ...) is created by CS people fed up with the C++ dumpster fire. So I don't know who is telling engineers that C++ is the future. And the perception that Fortran is an obsolete programming language is very strong, even within the engineering/technical disciplines that it was designed for. Sometimes this is due to sheer ignorance, but sometimes it is due to ancient Fortran 77 legacy code that people have to deal with. I sympathize with them, Fortran 77 code is terrible and needs to go away, but it should be modernized, not thrown out and replaced with C++. Think of the children! (and the memory leaks!)

Parting words of wisdom

Security tips when programming in C (2017 edition):

1) Stop typing

2) Delete what you've already typed

— ryan huber (@ryanhuber) June 21, 2017

See also

• Earth-GRAM 2016 is now available!
• Earth Global Reference Atmospheric Model (Earth-GRAM 2010) -- The last Fortran 90 release. [request here]
• F.W. Leslie, C.G. Justus, "The NASA Marshall Space Flight Center Earth Global Reference Atmospheric Model—2010 Version", NASA/TM—2011–216467, 2011
• ModelWeb Catalogue and Archive -- other atmosphere models listed on GSFC ModelWeb
• D. L. Johnson, R. Blocker, C. G. Justus, Global Reference Atmosphere Model (GRAM), NASA Tech Brief, MFS-28397, Jan 01, 1993

Fehlberg's Runge-Kutta Methods

Many of the important algorithms we use today in the space business have their origins in NASA's Apollo program. For example, the Runge-Kutta methods with stepsize control developed by Erwin Fehlberg (1911-1990). These are still used today for propagating spacecraft trajectories. Fehlberg was a German mathematician who ended up at Marshall Spaceflight Center in Huntsville, Alabama. Many of the original reports documenting these methods are publicly available on the NASA Technical Reports Server (see references below). Modern Fortran implementations of Fehlberg's RK7(8) and RK8(9) methods (and others) can be found in the Fortran Astrodynamics Toolkit.

See also

• Fehlberg, E., "Classical Fifth-, Sixth-, Seventh-, and Eighth-Order Runge-Kutta Formulas with Stepsize Control", NASA-TR-R-287, 1968
• Fehlberg, E., "Low-order classical Runge-Kutta formulas with stepsize control and their application to some heat transfer problems", NASA-TR-R-315, 1969
• Fehlberg, E., "Classical eight- and lower-order Runge-Kutta-Nystrom formulas with stepsize control for special second-order differential equations", NASA-TR-R-381, M-533, 1972
• Fehlberg, E., "Classical eighth- and lower-order Runge-Kutta-Nystrom formulas with a new stepsize control procedure for special second-order differential equations", NASA-TR-R-410, M-544, 1973
• Fehlberg, E., "Classical seventh-, sixth-, and fifth-order Runge-Kutta-Nystrom formulas with stepsize control for general second-order differential equations", NASA-TR-R-432, M-546, 1974

Directed Acyclic Graph Library

I released a new open source project on GitHub: DAGLIB, a modern Fortran library for manipulation of directed acyclic graphs (DAGs). This is based on some code I showed in a previous post. Right now, it's very basic, but you can use it to define DAGs, generate the topologically sorted order, and generate a "dot" file that can be used by GraphViz to visualize the DAG (such as the one shown at right).

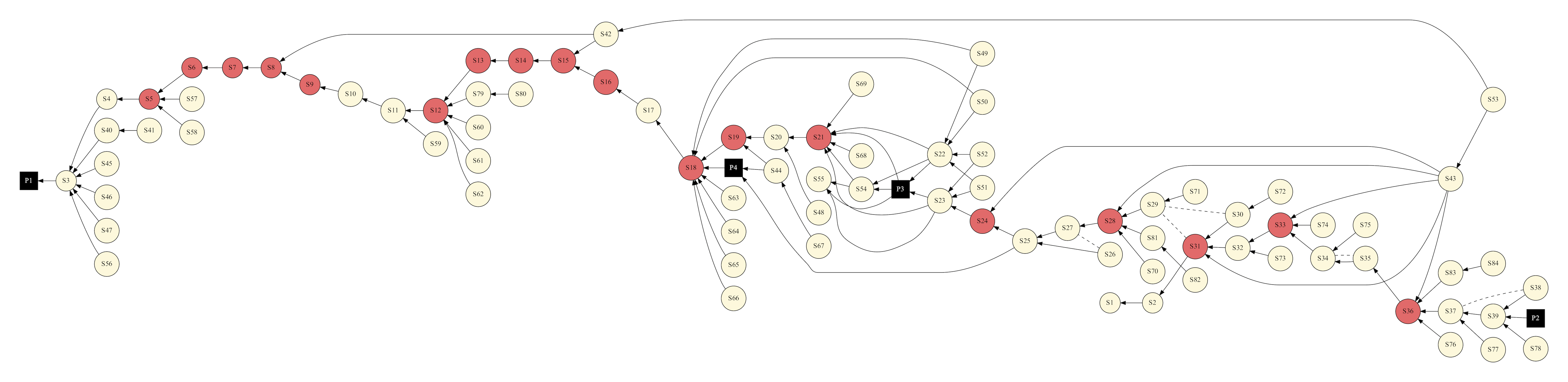
In my recent AIAA paper I showed the following DAG representing how we have designed the upcoming Orion EM-1 mission:

In this case, the DAG represents the dependencies among different mission attributes (which represent maneuvers, coast phases, constraints, other algorithms, etc). To simulate the entire end-to-end mission, each element must be evaluated in the correct order such that all the dependencies are met. In this same paper, we also discuss other algorithms and their implementation in modern Fortran which may be familiar to readers of this blog.

See also

1. J. Williams, R. D. Falck, and I. B. Beekman. "Application of Modern Fortran to Spacecraft Trajectory Design and Optimization", 2018 Space Flight Mechanics Meeting, AIAA SciTech Forum, (AIAA 2018-1451)
2. (Modern?) Fortran directed graphs library [comp.lang.fortran] May 6, 2016
3. JSON-Fortran GraphViz Example (how to generate a directed graph from a JSON structure), Apr 22, 2017
4. The Ins and Outs of NASA’s First Launch of SLS and Orion, NASA, Nov. 27, 2015

Binary Search

Binary search is a search algorithm that finds the position of a target value within a sorted array. The following binary search routine is taken from NASTRAN, a venerable finite element analysis program from NASA:

    SUBROUTINE BISLOC (*,ID,ARR,LEN,KN,JLOC)
C-----
C BINARY SEARCH - LOCATE KEY WORD 'ID' IN ARRAY 'ARR', 1ST ENTRY
C IF FOUND, 'JLOC' IS THE MATCHED POSITION IN 'ARR'
C IF NOT FOUND, NON-STANDARD RETURN
C I.E.
C ID = KEY WORD TO MATCH IN ARR. MATCH AGAINST 1ST COL OF ARR
C ARR = ARRAY TO SEARCH. ARR(ROW,COL)
C LEN = LENGTH OF EACH ENTRY IN ARRAY. LEN=ROW
C KN = NUMBER OF ENTRIES IN THE ARR. KN =COL
C JLOC= POINTER RETURNED - FIRST WORD OF ENTRY. MATCHED ROW
C-----
C
    INTEGER ARR(1)
    DATA ISWTCH / 16 /
C
    JJ = LEN - 1
    IF (KN .LT. ISWTCH) GO TO 120
    KLO = 1
    KHI = KN
10  K = (KLO+KHI+1)/2
20  J = K*LEN - JJ
    IF (ID-ARR(J)) 30,90,40
30  KHI = K
    GO TO 50
40  KLO = K
50  IF (KHI-KLO -1) 100,60,10
60  IF (K .EQ. KLO) GO TO 70
    K = KLO
    GO TO 80
70  K = KHI
80  KLO = KHI
    GO TO 20
90  JLOC = J
    RETURN
100 JLOC = KHI*LEN - JJ
    J = KN *LEN - JJ
    IF (ID .GT.ARR(J)) JLOC = JLOC + LEN
110 RETURN 1
C
C SEQUENTIAL SEARCH MORE EFFICIENT
C
120 KHI = KN*LEN - JJ
    DO 130 J = 1,KHI,LEN
    IF (ARR(J)-ID) 130,90,140
130 CONTINUE
    JLOC = KHI + LEN
    GO TO 110
140 JLOC = J
    GO TO 110
    END

As you can see, it is a scene of FORTRAN 66 horrors! However, it can be refactored into a nice modern Fortran routine like so:

pure function bisloc(id,arr) result(jloc)

!! binary search of a sorted array.

implicit none

integer,intent(in) :: id
    !! key word to match in `arr`
integer,dimension(:),intent(in) :: arr
    !! array to search (it is
    !! assumed to be sorted)
integer :: jloc
    !! the first matched index in 'arr'
    !! (if not found, 0 is returned)

integer :: j,k,khi,klo,n
integer,parameter :: iswtch = 16

n = size(arr)
jloc = 0

if ( n<iswtch ) then

    ! sequential search more efficient

    do j = 1 , n
        if ( arr(j)==id ) then
            jloc = j
            return
        else if (arr(j)>id) then
            return ! error
        end if
    end do
    return ! error

else

    klo = 1
    khi = n
    k = (klo+khi+1)/2
    do
        j = k
        if ( id<arr(j) ) then
            khi = k
        else if ( id==arr(j) ) then
            jloc = j
            return
        else
            klo = k
        end if
        if ( khi-klo<1 ) then
            return ! error
        else if ( khi-klo==1 ) then
            if ( k==klo ) then
                k = khi
            else
                k = klo
            end if
            klo = khi
        else
            k = (klo+khi+1)/2
        end if
    end do

end if

end function bisloc

I did change a couple of things:

• The original routine was using an obsolete alternate return (note the * argument) for an error condition. The new one just returns 0 if there is an error.
• The original routine was passing in the array as a vector and treating it like a matrix (it's either searching a row or column of this matrix, I admit I had a hard time telling). The new version assumes the input is a rank-1 array. You can pass in whatever matrix slices you want (say a column: a(:,1) or a row: a(1,:)).
• I also made it a pure function, because that's how I roll.

Note that NASTRAN was released under the NASA Open Source Agreement version 1.3, a somewhat unusual open source license. It isn't considered a "free" license by the FSF since it includes a statement requiring changes to be your "original creation".

Unfortunately, the trend at NASA (and elsewhere) is to declare old Fortran code like this to be totally unmaintainable. So, instead of refactoring them into modern Fortran standards, they are thrown away and rewritten from scratch using a more "modern" language like C++ (whose roots go back to 1972!).

See also

• NASTRAN-95 at NASA's GitHub.

C++ vs Fortran (Part 2)

Here is some C++ code (from actual NASA software):

aTilde[ 0] = aTilde[ 1] = aTilde[ 2] =
aTilde[ 3] = aTilde[ 4] = aTilde[ 5] =
aTilde[ 6] = aTilde[ 7] = aTilde[ 8] =
aTilde[ 9] = aTilde[10] = aTilde[11] =
aTilde[12] = aTilde[13] = aTilde[14] =
aTilde[15] = aTilde[16] = aTilde[17] =
aTilde[18] = aTilde[19] = aTilde[20] =
aTilde[21] = aTilde[22] = aTilde[23] =
aTilde[24] = aTilde[25] = aTilde[26] =
aTilde[27] = aTilde[28] = aTilde[29] =
aTilde[30] = aTilde[31] = aTilde[32] =
aTilde[33] = aTilde[34] = aTilde[35] = 0.0;

Here is the same code translated to Fortran:

aTilde = 0.0

😀

References

• N. Maclaren, Why (and Why Not) to Use Fortran Instead of C++, Matlab, Python etc, University of Cambridge Computing Service, June 2012.
• Daniel C. Elton, Why physicists still use Fortran, July 16, 2015.