
The rocket equation describes the basic principles of a rocket in the absence of external forces. Various forms of this equation relate the following fundamental parameters:
- the engine thrust (\(T\)),
- the engine specific impulse (\(I_{sp}\)),
- the engine exhaust velocity (\(c\)),
- the initial mass (\(m_i\)),
- the final mass (\(m_f\)),
- the burn duration (\(\Delta t\)), and
- the effective delta-v (\(\Delta v\)) of the maneuver.
The rocket equation is:
- \(\Delta v = c \ln \left( \frac{m_i}{m_f} \right)\)
The engine specific impulse is related to the engine exhaust velocity by: \(c = I_{sp} g_0\), where \(g_0\) is the standard Earth gravitational acceleration at sea level (defined to be exactly 9.80665 \(m/s^2\)). The thrust is related to the mass flow rate (\(\dot{m}\)) of the engine by: \(T = c \dot{m}\). This can be used to compute the duration of the maneuver as a function of the \(\Delta v\):
- \(\Delta t = \frac{c m_i}{T} \left( 1 - e^{-\frac{\Delta v}{c}} \right)\)
A Fortran module implementing these equations is given below.
module rocket_equation
use,intrinsic :: iso_fortran_env, only: wp => real64
implicit none
!two ways to compute effective delta-v
interface effective_delta_v
procedure :: effective_dv_1,effective_dv_2
end interface effective_delta_v
real(wp),parameter,public :: g0 = 9.80665_wp ![m/s^2]
contains
pure function effective_dv_1(c,mi,mf) result(dv)
real(wp) :: dv ! effective delta v [m/s]
real(wp),intent(in) :: c ! exhaust velocity [m/s]
real(wp),intent(in) :: mi ! initial mass [kg]
real(wp),intent(in) :: mf ! final mass [kg]
dv = c*log(mi/mf)
end function effective_dv_1
pure function effective_dv_2(c,mi,T,dt) result(dv)
real(wp) :: dv ! delta-v [m/s]
real(wp),intent(in) :: c ! exhaust velocity [m/s]
real(wp),intent(in) :: mi ! initial mass [kg]
real(wp),intent(in) :: T ! thrust [N]
real(wp),intent(in) :: dt ! duration of burn [sec]
dv = -c*log(1.0_wp-(T*dt)/(c*mi))
end function effective_dv_2
pure function burn_duration(c,mi,T,dv) result(dt)
real(wp) :: dt ! burn duration [sec]
real(wp),intent(in) :: c ! exhaust velocity [m/s]
real(wp),intent(in) :: mi ! initial mass [kg]
real(wp),intent(in) :: T ! engine thrust [N]
real(wp),intent(in) :: dv ! delta-v [m/s]
dt = (c*mi)/T*(1.0_wp-exp(-dv/c))
end function burn_duration
pure function final_mass(c,mi,dv) result(mf)
real(wp) :: mf ! final mass [kg]
real(wp),intent(in) :: c ! exhaust velocity [m/s]
real(wp),intent(in) :: mi ! initial mass [kg]
real(wp),intent(in) :: dv ! delta-v [m/s]
mf = mi/exp(dv/c)
end function final_mass
end module rocket_equation
References
- J.E. Prussing, B.A. Conway, "Orbital Mechanics", Oxford University Press, 1993.
Complex step differentiation is a method for estimating the derivative of a function \(f(x)\) using the equation:
- \(f'(x) \approx \frac{ Im[f(x + ih)] }{h}\)
Unlike finite-difference formulas, the complex-step formula does not suffer from roundoff errors due to subtraction, so a very small value of the step size \(h\) can be used, producing a much more accurate derivative. The example shown below is for the function: \(f(x) = e^x + \sin(x)\). The derivative error is compared to three finite-difference formulas:
- \(f'(x) \approx \frac{f(x+h) - f(x)}{h}\) (Two-point forward difference)
- \(f'(x) \approx \frac{f(x+h) - f(x-h)}{2h}\) (Two-point central difference)
- \(f'(x) \approx \frac{f(x-2h) -8 f(x-h) + 8 f(x+h) - f(x+2h) }{12 h}\) (Four-point central difference)
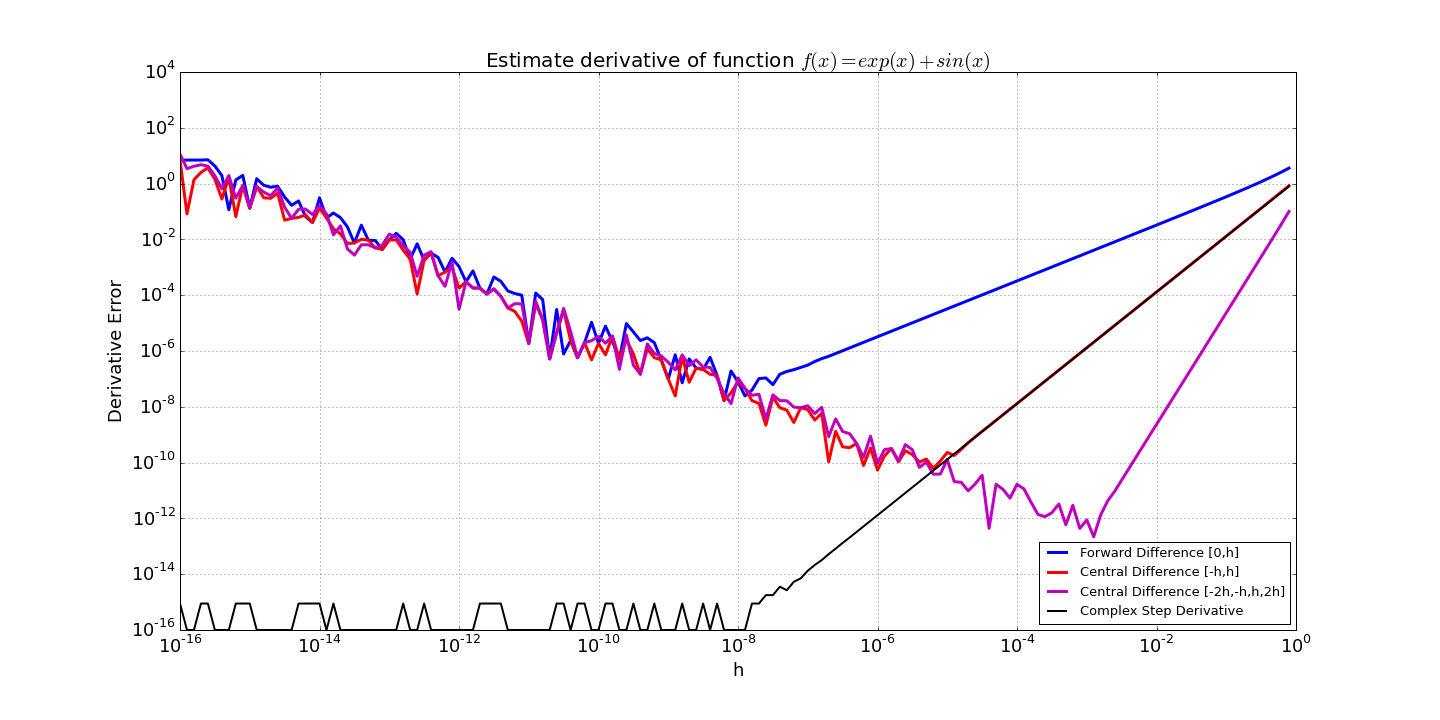
For large values of \(h\), truncation error dominates. The finite-difference error decreases as \(h\) is decreased, until roundoff error begins to dominate (around \(10^{-8}\) for the forward difference, \(10^{-5}\) for the 2-point central difference, and \(10^{-3}\) for the 4-point central difference). The complex-step estimate, however, can produce a derivative estimate to machine precision for any value of \(h < 10^{-8}\).
See also
- J.R.R.A. Martins, I.M. Kroo, J.J. Alonso, "An Automated Method for Sensitivity Analysis using Complex Variables", AIAA-2000-0689.
- complex_step.f90 in the Fortran Astrodynamics Toolkit.
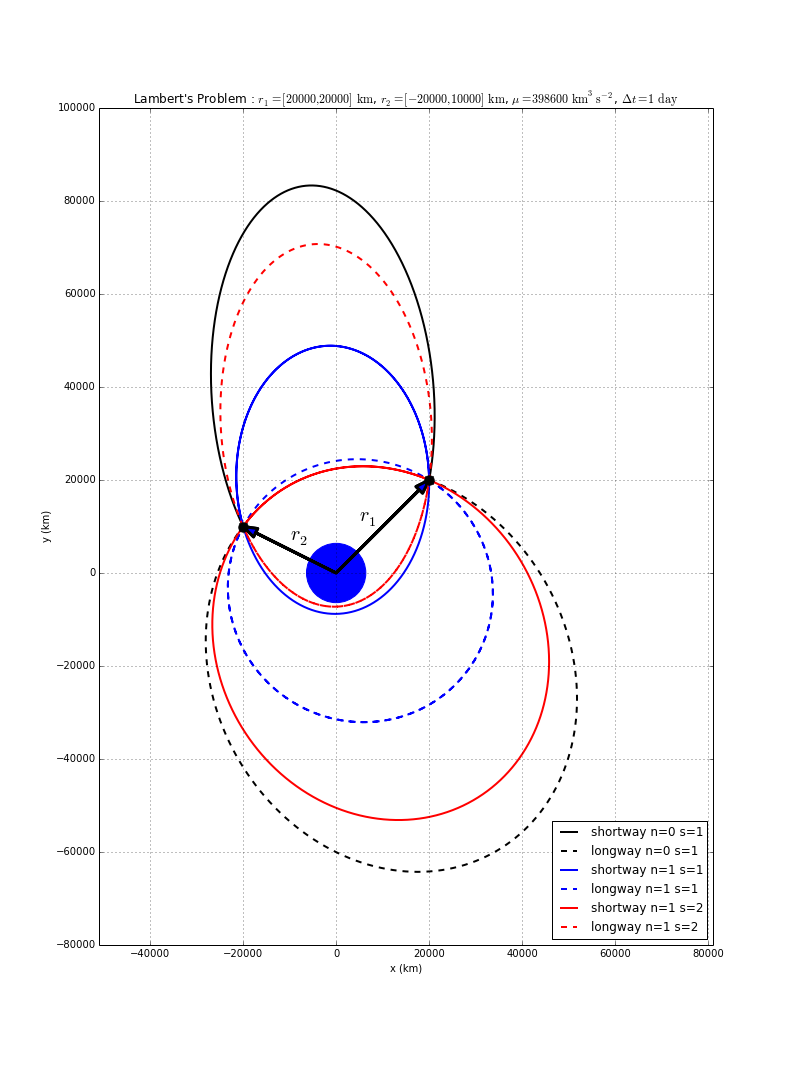
Lambert's problem is to solve for the orbit transfer that connects two position vectors in a given time of flight. It is one of the basic problems of orbital mechanics, and was solved by Swiss mathematician Johann Heinrich Lambert.
A standard Fortran 77 implementation of Lambert's problem was presented by Gooding [1]. A modern update to this implementation is included in the Fortran Astrodynamics Toolkit, which also includes a newer algorithm from Izzo [2].
There can be multiple solutions to Lambert's problem, which are classified by:
- Direction of travel (i.e., a "short" way or "long" way transfer).
- Number of complete revolutions (N=0,1,...). For longer flight times, solutions exist for larger values of N.
- Solution number (S=1 or S=2). The multi-rev cases can have two solutions each.
In the example shown here, there are 6 possible solutions:
References
- R.H, Gooding. "A procedure for the solution of Lambert's orbital boundary-value problem", Celestial Mechanics and Dynamical Astronomy, Vol. 48, No. 2, 1990.
- D. Izzo, "Revisiting Lambert’s problem", Celestial Mechanics and Dynamical Astronomy, Oct. 2014.
The ISO_C_BINDING intrinsic module and the BIND attribute introduced in Fortran 2003 are very handy for producing standard and portable Fortran code that interacts with C code. The example given here shows how to use the popen, fgets, and pclose routines from the C standard library to pipe the result of a shell command into a Fortran allocatable string.
module pipes_module
use,intrinsic :: iso_c_binding
implicit none
private
interface
function popen(command, mode) bind(C,name='popen')
import :: c_char, c_ptr
character(kind=c_char),dimension(*) :: command
character(kind=c_char),dimension(*) :: mode
type(c_ptr) :: popen
end function popen
function fgets(s, siz, stream) bind(C,name='fgets')
import :: c_char, c_ptr, c_int
type (c_ptr) :: fgets
character(kind=c_char),dimension(*) :: s
integer(kind=c_int),value :: siz
type(c_ptr),value :: stream
end function fgets
function pclose(stream) bind(C,name='pclose')
import :: c_ptr, c_int
integer(c_int) :: pclose
type(c_ptr),value :: stream
end function pclose
end interface
public :: c2f_string, get_command_as_string
contains
!**********************************************
! convert a C string to a Fortran string
!**********************************************
function c2f_string(c) result(f)
implicit none
character(len=*),intent(in) :: c
character(len=:),allocatable :: f
integer :: i
i = index(c,c_null_char)
if (i<=0) then
f = c
else if (i==1) then
f = ''
else if (i>1) then
f = c(1:i-1)
end if
end function c2f_string
!**********************************************
! return the result of the command as a string
!**********************************************
function get_command_as_string(command) result(str)
implicit none
character(len=*),intent(in) :: command
character(len=:),allocatable :: str
integer,parameter :: buffer_length = 1000
type(c_ptr) :: h
integer(c_int) :: istat
character(kind=c_char,len=buffer_length) :: line
str = ''
h = c_null_ptr
h = popen(command//c_null_char,'r'//c_null_char)
if (c_associated(h)) then
do while (c_associated(fgets(line,buffer_length,h)))
str = str//c2f_string(line)
end do
istat = pclose(h)
end if
end function get_command_as_string
end module pipes_module
A example use of this module is:
program test
use pipes_module
implicit none
character(len=:),allocatable :: res
res = get_command_as_string('uname')
write(*,'(A)') res
res = get_command_as_string('ls -l')
write(*,'(A)') res
end program test
References
- C interop to popen, comp.lang.fortran, 12/2/2009.

The Midpoint circle algorithm is a clever and efficient way of drawing a circle using only addition, subtraction, and bit shifts. It is based on the Bresenham line algorithm developed by Jack Bresenham in 1962 at IBM.
The algorithm was also independently discovered by Apple programmer Bill Atkinson in 1981 when developing QuickDraw for the original Macintosh.
A Fortran implementation is given below (which was used to draw the circle shown here, which has a radius of 7 pixels):
subroutine draw_circle(x0, y0, radius, color)
implicit none
integer,intent(in) :: x0, y0, radius, color
integer :: x,y,err
x = radius
y = 0
err = 1-x
do while (x >= y)
call color_pixel( x + x0, y + y0, color)
call color_pixel( y + x0, x + y0, color)
call color_pixel( -x + x0, y + y0, color)
call color_pixel( -y + x0, x + y0, color)
call color_pixel( -x + x0, -y + y0, color)
call color_pixel( -y + x0, -x + y0, color)
call color_pixel( x + x0, -y + y0, color)
call color_pixel( y + x0, -x + y0, color)
y = y + 1
if (err<0) then
err = err + 2 * y + 1
else
x = x - 1
err = err + 2 * (y - x + 1)
end if
end do
end subroutine draw_circle
References
- Jack E. Bresenham, "Algorithms for Computer Control of a Digital Plotter", IBM System Journal, 1965.
Fortran90.org has a nice page showing side-by-side comparisons of the same code in both NumPy and Fortran. Aside from a few weird quirks (see the array slice examples), Python code should be easily understandable by a Fortran programmer.
Fortran 2003 was a significant update to Fortran 95 (probably something on the order of the update from C to C++). It brought Fortran into the modern computing world with the addition of object oriented programming features such as type extension and inheritance, polymorphism, dynamic type allocation, and type-bound procedures.
The following example shows an implementation of an object oriented class to perform numerical integration of a user-defined function using a Runge-Kutta method (in this case RK4). First, an abstract rk_class is defined, which is then extended to create the RK4 class by associating the deferred step method to rk4. Other RK classes could also be created in a similar manner. In order to use the class, it is only necessary to set n (the number of variables in the state vector) and f (the user-supplied derivative function), and then call the integrate method.
module rk_module
use, intrinsic :: iso_fortran_env, wp => real64 !double precision reals
implicit none
real(wp),parameter :: zero = 0.0_wp
!main integration class:
type,abstract,public :: rk_class
private
!user specified number of variables:
integer :: n = 0
!user-specified derivative function:
procedure(deriv_func),pointer :: f => null()
contains
procedure,non_overridable,public :: integrate !main integration routine
procedure(step_func),deferred :: step !the step routine for the selected method
end type rk_class
!extend the abstract class to create an RK4 method:
! [all we need to do is set the step function]
type,extends(rk_class),public :: rk4_class
contains
procedure :: step => rk4
end type rk4_class
interface
subroutine deriv_func(me,t,x,xdot) !derivative function
import :: rk_class,wp
implicit none
class(rk_class),intent(inout) :: me
real(wp),intent(in) :: t
real(wp),dimension(me%n),intent(in) :: x
real(wp),dimension(me%n),intent(out) :: xdot
end subroutine deriv_func
subroutine step_func(me,t,x,h,xf) !rk step function
import :: rk_class,wp
implicit none
class(rk_class),intent(inout) :: me
real(wp),intent(in) :: t
real(wp),dimension(me%n),intent(in) :: x
real(wp),intent(in) :: h
real(wp),dimension(me%n),intent(out) :: xf
end subroutine step_func
end interface
contains
subroutine integrate(me,t0,x0,h,tf,xf)
! main integration routine
implicit none
class(rk_class),intent(inout) :: me
real(wp),intent(in) :: t0
real(wp),dimension(me%n),intent(in) :: x0
real(wp),intent(in) :: h
real(wp),intent(in) :: tf
real(wp),dimension(me%n),intent(out) :: xf
real(wp) :: t,dt,t2
real(wp),dimension(me%n) :: x
logical :: last
if (h==zero) then
xf = x0
else
t = t0
x = x0
dt = h
do
t2 = t + dt
last = ((dt>=zero .and. t2>=tf) .or. & !adjust last time step
(dt<zero .and. t2<=tf)) !
if (last) dt = tf-t !
call me%step(t,x,dt,xf)
if (last) exit
x = xf
t = t2
end do
end if
end subroutine integrate
subroutine rk4(me,t,x,h,xf)
! Take one Runge Kutta 4 integration step: t -> t+h (x -> xf)
implicit none
class(rk4_class),intent(inout) :: me
real(wp),intent(in) :: t
real(wp),dimension(me%n),intent(in) :: x
real(wp),intent(in) :: h
real(wp),dimension(me%n),intent(out) :: xf
!local variables:
real(wp),dimension(me%n) :: f1,f2,f3,f4
real(wp) :: h2
!parameters:
real(wp),parameter :: half = 0.5_wp
real(wp),parameter :: six = 6.0_wp
h2 = half*h
call me%f(t,x,f1)
call me%f(t+h2,x+h2*f1,f2)
call me%f(t+h2,x+h2*f2,f3)
call me%f(t+h,x+h*f3,f4)
xf = x + h*(f1+f2+f2+f3+f3+f4)/six
end subroutine rk4
end module rk_module
An example use of this module follows. Here, we are integrating the equations of motion of a spacecraft in Earth orbit, using two-body assumptions: \(\ddot{\mathbf{r}} = -\frac{\mu}{r^3}\mathbf{r}\)
The rk4_class is extended to create a new spacecraft class, which contains the data required by the derivative routine (in this case, simply the central body gravitational parameter mu). A more complicated version could also include spherical harmonic gravity, solar radiation pressure, atmospheric drag, engine thrust, etc. Note that the select type statement is necessary in the derivative routine in order to access the data from the extended type.
program main
use rk_module
!spacecraft propagation type:
! extend the rk class to include data used in the deriv routine
type,extends(rk4_class) :: spacecraft
real(wp) :: mu = zero ! central body gravitational
! parameter (km^3/s^2)
end type spacecraft
integer,parameter :: n=6 !number of state variables
type(spacecraft) :: s
real(wp) :: t0,tf,x0(n),dt,xf(n)
!constructor:
s = spacecraft(n=n,f=twobody,mu=398600.436233_wp) !main body is Earth
!initial conditions:
x0 = [10000.0_wp,10000.0_wp,10000.0_wp,& !initial state [x,y,z] (km)
1.0_wp,2.0_wp,3.0_wp] ! [vx,vy,yz] (km/s)
t0 = zero !initial time (sec)
dt = 10.0_wp !time step (sec)
tf = 1000.0_wp !final time (sec)
call s%integrate(t0,x0,dt,tf,xf)
write(*,'(A/,*(F15.6/))') 'Final state:',xf
contains
subroutine twobody(me,t,x,xdot)
! derivative routine for two-body orbit propagation
implicit none
class(rk_class),intent(inout) :: me
real(wp),intent(in) :: t
real(wp),dimension(me%n),intent(in) :: x
real(wp),dimension(me%n),intent(out) :: xdot
real(wp),dimension(3) :: r,v,a_grav
real(wp) :: rmag
select type (me)
class is (spacecraft)
r = x(1:3)
v = x(4:6)
rmag = norm2(r)
a_grav = -me%mu/rmag**3 * r !accel. due to gravity
xdot(1:3) = v
xdot(4:6) = a_grav
end select
end subroutine twobody
end program main
The result is:
Final state: 10667.963305 11658.055962 12648.148619 0.377639 1.350074 2.322509
See also
- Object-Oriented Programming in Fortran 2003 Part 1: Code Reusability, PGI Insider, Feb. 2011.
- Object-Oriented Programming in Fortran 2003 Part 2: Data Polymorphism, PGI Insider, June 2011.
- Fortran Astrodynamics Toolkit (Github)
Intel has released version 15 of their Fortran compiler (the product formerly known as Intel Visual Fortran, and now part of the confusingly-named "Intel Parallel Studio XE 2015 Composer Edition", is an update to the v14 release which was called "Intel Composer XE 2013 SP1"). The big news is that it now includes full support for the Fortran 2003 standard. This release also adds support for the BLOCK construct and EXECUTE_COMMAND_LINE intrinsic subroutine from Fortran 2008.
See also
- Compiler support for the Fortran 2003 Standard

The Computus is the algorithm for the calculation of the date of Easter. The following is a simple Fortran subroutine of the Computus, using the "Meeus/Jones/Butcher" Gregorian Easter algorithm. Note that this subroutine makes use of Fortran integer division.
subroutine easter(year,month,day)
!Compute the date of Gregorian Easter,
! using the "Meeus/Jones/Butcher" algorithm
implicit none
integer,intent(in) :: year
integer,intent(out) :: month,day
integer :: a,b,c,d,e,f,g,h,i,k,l,m
a = mod(year,19)
b = year/100
c = mod(year,100)
d = b/4
e = mod(b,4)
f = (b+8)/25
g = (b-f+1)/3
h = mod((19*a+b-d-g+15),30)
i = c/4
k = mod(c,4)
l = mod((32+2*e+2*i-h-k),7)
m = (a+11*h+22*l)/451
month = (h+l-7*m+114)/31
day = mod(h+l-7*m+114,31)+1
end subroutine easter
The sequence of dates repeat themselves over a cycle of 5,700,000 years. The following histogram shows the percentage occurrence of each date (from March 22nd to April 25th), over the entire cycle:
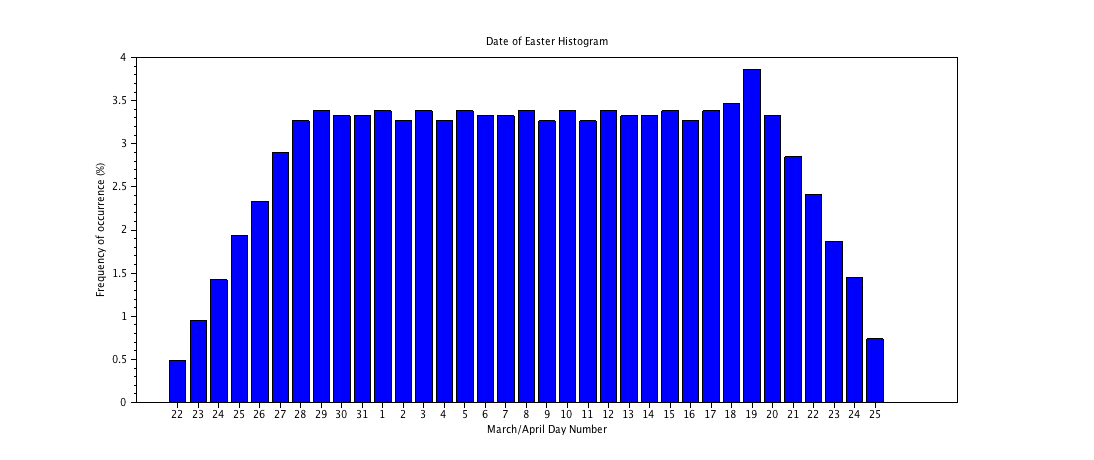
See also
- D. Steel, "Marking Time: The Epic Quest to Invent the Perfect Calendar", Wiley, 1999.
- J. R. Stockton, "The Calculation of Easter Sunday after the Book of Common Prayer of the Church of England".
Old style fixed-form Fortran code (commonly called FORTRAN 77 style) was replaced by free-form style in 1991 with the introduction of the Fortran 90 standard. In spite of this, fixed-form code can still be found in legacy projects, and there are some people who still write it for whatever reason (possibly unaware that a better format exists). There are also a large number of high-quality legacy fixed-form code libraries from back in the day that still work great. All modern Fortran compilers accept both fixed and free-form code, but there is very little reason for new fixed-form code to be written today. Also, it is often convenient to convert old-style code to free-format if it is going to be maintained or upgraded by a programmer in the present day. The following list provides links to several free tools to convert fixed-form code to free-form code (there are also several commercially-available solutions):
See also
- Source Form Just Wants to be Free
- Modernizing Old Fortran





