Degenerate Conic

Revenge of the Animated GIF

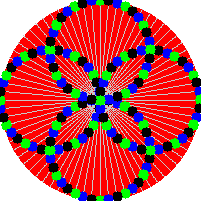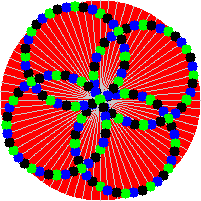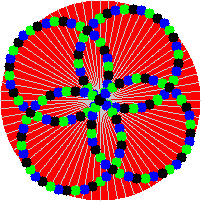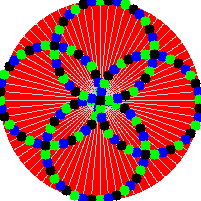
Yes, now animated GIFs can be created using only Fortran code. I present FGIF, now on GitHub. It is a modified and updated version of the public domain code found on the Fortran Wiki. It was used to create the image shown here (which is an example of a circle illusion).

For more information on the GIF format, see:

• What's In A GIF
• GIF Format

It was interesting to discover that animated GIFs are actually a Netscape extension to the GIF file format. If you open any animated GIF in a hex editor, you will find the string "NETSCAPE2.0".

SPICE N65 Released

JPL just released a new version of the SPICE Toolkit (N65). According to the What's New page, changes include:

• support for some new environments and termination of some old environments
• new Geometry Finder (GF) interfaces -- illumination angle search, phase angle search, user-defined binary quantity search
• new high-level SPK APIs allowing one to specify the observer or target as a location with a constant position and velocity rather than as an ephemeris object
• new high-level APIs that check for occultation and in-Field-Of-View (FOV) conditions
• new high-level illumination angle routines
• new high-level reference frame transformation routine
• new high-level coordinate system transformation routine for states
• many Icy and Mice APIs that were formerly available only in SPICELIB and CSPICE
• new data types: SPK (19, 20, 21), PCK (20), and CK (6)
• performance improvements in the range of 10-50 percent for some types of use
• ability to load up to 5000 kernels
• increased buffers in the POOL and in SPK and CK segment search subsystems
• new built-in body name/ID code mappings and body-fixed reference frames
• a significant upgrade of utility SPKDIFF including the ability to sample SPK data
• updates to other toolkit utilities -- BRIEF, CKBRIEF, FRMDIFF, MKSPK, MSOPCK
• bug fixes in Toolkit and utility programs

json-fortran 1.0.0

I just tagged the 1.0.0 release of json-fortran. You're welcome, interwebs.

Rodrigues' Rotation Formula

Rodrigues' rotation formula can be used to rotate a vector \(\mathbf{v}\) a specified angle \(\theta\) about a specified rotation axis \(\mathbf{k}\):

A Fortran routine to accomplish this (taken from the vector module in the Fortran Astrodynamics Toolkit) is:

subroutine rodrigues_rotation(v,k,theta,vrot)

implicit none

real(wp),dimension(3),intent(in) :: v !vector to rotate
real(wp),dimension(3),intent(in) :: k !rotation axis
real(wp),intent(in) :: theta !rotation angle [rad]
real(wp),dimension(3),intent(out) :: vrot !result

real(wp),dimension(3) :: khat
real(wp) :: ct,st

ct = cos(theta)
st = sin(theta)
khat = unit(k)

vrot = v*ct + cross(khat,v)*st + &
khat*dot_product(khat,v)*(one-ct)

end subroutine rodrigues_rotation

This operation can also be converted into a rotation matrix, using the equation:

Where the matrix \([\hat{\mathbf{k}}\times]\) is the skew-symmetric cross-product matrix and \(\mathbf{v}_\mathrm{rot} = \mathbf{R} \mathbf{v}\).

References

1. Rotation Formula [Mathworld]
2. Rodrigues' Rotation Formula [Mathworld]
3. Do We Really Need Quaternions? [Gamedev.net]
4. R. T. Savely, B. F. Cockrell, and S. Pines, "Apollo Experience Report -- Onboard Navigational and Alignment Software", NASA TN D-6741, March 1972. See the Appendix by P. F. Flanagan and S. Pines, "An Efficient Method for Cartesian Coordinate Transformations".

GCC 4.9.1

GCC 4.9.1 has been released. The big news for Fortran users is that OpenMP 4.0 is now supported in gfortran.

Fortran Astrodynamics Toolkit

I'm starting a new project on GitHub: the Fortran Astrodynamics Toolkit. Hardly anyone is developing open source orbital mechanics software for modern Fortran, so the time has come. Most of the code from this blog will eventually find its way there. My goal is to include modern Fortran implementations of all the standard orbital mechanics algorithms such as:

• Lambert solvers
• Kepler propagators
• ODE solvers (Runge-Kutta, Nyström, Adams)
• Orbital element conversions

Then we'll see where it goes from there. The code will be released under a permissive BSD style license.

Unique

Here is a simple Fortran subroutine to return only the unique values in a vector (inspired by Matlab's unique function). Note, this implementation is for integer arrays, but could easily be modified for any type. This code is not particularly optimized, so there may be a more efficient way to do it. It does demonstrate Fortran array transformational functions such as pack and count. Note that to duplicate the Matlab function, the output array must also be sorted.

subroutine unique(vec,vec_unique)  
! Return only the unique values from vec.

implicit none

integer,dimension(:),intent(in) :: vec  
integer,dimension(:),allocatable,intent(out) :: vec_unique

integer :: i,num  
logical,dimension(size(vec)) :: mask

mask = .false.

do i=1,size(vec)

    !count the number of occurrences of this element:  
    num = count( vec(i)==vec )

    if (num==1) then  
        !there is only one, flag it:  
        mask(i) = .true.  
    else  
        !flag this value only if it hasn't already been flagged:  
        if (.not. any(vec(i)==vec .and. mask) ) mask(i) = .true.  
    end if

end do

!return only flagged elements:  
allocate( vec_unique(count(mask)) )  
vec_unique = pack( vec, mask )

!if you also need it sorted, then do so.  
! For example, with slatec routine:  
!call ISORT (vec_unique, [0], size(vec_unique), 1)

end subroutine unique  

C++ vs Fortran

I agree with everything said in this article: My Corner of the World: C++ vs Fortran. I especially like the bit contrasting someone trying to learn C++ for the first time in order to do some basic linear algebra (like a matrix multiplication). Of course, in Fortran, this is a built-in part of the language:

matrix_c = matmul(matrix_a, matrix_b)  

Whereas, for C++:

The bare minimum for doing the same exercise in C++ is that you have to get your hands on a library that does what you want. So you have to know about the existence of Eigen or another library. Then you have to figure out how to call it. Then you have to figure out how to link to an external library. And the documentation is probably not that helpful. There are friendly C++ users for sure. It's just that you won't have a clue what they're telling you to do. They'll be telling you to set up a makefile. They'll be recommending that you look at Boost and talking about how great it is and you'll be all WTF.

And before you use that C++ library, are you really sure you won't end up with a memory leak? Do you even know what a memory leak is?

Modern Fortran References

In the last few years, a number of excellent books have been published about modern Fortran:

• R. J. Hanson, Numerical Computing With Modern Fortran, SIAM-Society for Industrial and Applied Mathematics, 2013.
• A. Markus, Modern Fortran in Practice, Cambridge University Press, 2012.
• M. Metcalf, J. Reid, M. Cohen, Modern Fortran Explained, Oxford University Press, 2011.
• N. S. Clerman, W. Spector, Modern Fortran: Style and Usage, Cambridge University Press, 2011.

In addition, other more general-purpose references on modern programming concepts (such as object-oriented programming and high performance computing) tailored to the Fortran programmer are:

• D. Rouson, J. Xia, X. Xu, Scientific Software Design: The Object-Oriented Way, Cambridge University Press, 2011.
• G. Hager, G. Wellein, Introduction to High Performance Computing for Scientists and Engineers, CRC Press, 2011.

All of these are highly recommended, especially if you want to learn modern Fortran for the first time. Under no circumstances should you purchase any Fortran book with the numbers "77", "90", or "95" in the title.

Sorting with Magic Numbers

Updated July 7, 2014

Poorly commented sourcecode is one of my biggest pet peeves. Not only should the comments explain what the routine does, but where the algorithm came from and what its limitations are. Consider ISORT, a non-recursive quicksort routine from SLATEC, written in 1976. In it, we encounter the following code:

R = 0.375E0
...
IF (R .LE. 0.5898437E0) THEN
    R = R+3.90625E-2
ELSE
    R = R-0.21875E0
ENDIF

What are these magic numbers? An internet search for "0.5898437" yields dozens of hits, many of them different versions of this algorithm translated into various other programming languages (including C, C++, and free-format Fortran). Note: the algorithm here is the same one, but also prefaces this code with the following helpful comment:

! And now...Just a little black magic...

Frequently, old code originally written in single precision can be improved on modern computers by updating to full-precision constants (replacing 3.14159 with a parameter computed at compile time as acos(-1.0_wp) is a classic example). Is this the case here? Sometimes WolframAlpha is useful in these circumstances. It tells me that a possible closed form of 0.5898437 is: \(\frac{57}{100\pi}+\frac{13\pi}{100} \approx 0.58984368009\). Hmmmmm... The reference given in the header is no help [1], it doesn't contain this bit of code at all.

It turns out, what this code is doing is generating a pseudorandom number to use as the pivot element in the quicksort algorithm. The code produces the following repeating sequence of values for R:

0.375
0.4140625
0.453125
0.4921875
0.53125
0.5703125
0.609375
0.390625
0.4296875
0.46875
0.5078125
0.546875
0.5859375
0.625
0.40625
0.4453125
0.484375
0.5234375
0.5625
0.6015625
0.3828125
0.421875
0.4609375
0.5
0.5390625
0.578125
0.6171875
0.3984375
0.4375
0.4765625
0.515625
0.5546875
0.59375

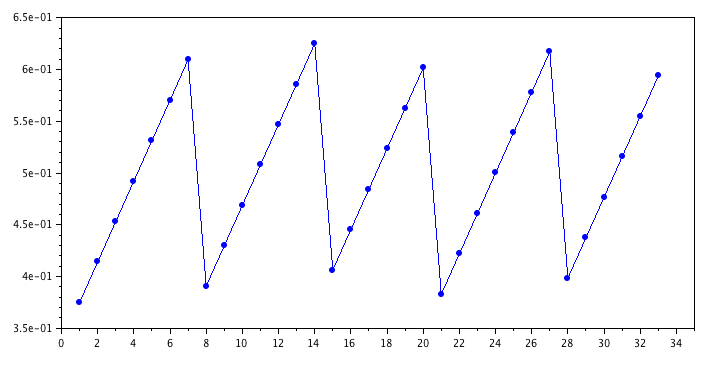
This places the pivot point near the middle of the set. The source of this scheme is from Reference [2], and is also mentioned in Reference [3]. According to [2]:

These four decimal constants, which are respectively 48/128, 75.5/128, 28/128, and 5/128, are rather arbitrary.

The other magic numbers in this routine are the dimensions of these variables:

INTEGER IL(21), IU(21)

These are workspace arrays used by the subroutine, since it does not employ recursion. But, since they have a fixed size, there is a limit to the size of the input array this routine can sort. What is that limit? You would not know from the documentation in this code. You have to go back to the original reference [1] (where, in fact, these arrays only had 16 elements). There, it explains that the arrays IL(K) and IU(K) permit sorting up to \(2^{k+1}-1\) elements (131,071 elements for the k=16 case). With k=21, that means the ISORT routine will work for up to 4,194,303 elements. So, keep that in mind if you are using this routine.

There are many other implementations of the quicksort algorithm (which was declared one of the top 10 algorithms of the 20th century). In the LAPACK quicksort routine DLASRT, k=32 and the "median of three" method is used to select the pivot. The quicksort method in R is the same algorithm as ISORT, except that k=40 (this code also has the advantage of being properly documented, unlike the other two).

References

1. R. C. Singleton, "Algorithm 347: An Efficient Algorithm for Sorting With Minimal Storage", Communications of the ACM, Vol. 12, No. 3 (1969).
2. R. Peto, "Remark on Algorithm 347", Communications of the ACM, Vol. 13 No. 10 (1970).
3. R. Loeser, "Survey on Algorithms 347, 426, and Quicksort", ACM Transactions on Mathematical Software (TOMS), Vol. 2 No. 3 (1976).