Degenerate Conic

JSON-Fortran 5.3.0

JSON-Fortran 5.3.0 is out. This release includes a few minor bug fixes and a couple of new features. For one thing, it is now possible to easily build or modify a JSON structure without using pointer variables. Here's an example:

program test

use json_module, rk=>json_rk

implicit none

type(json_file) :: f

call f%initialize()

call f%add('name', 'test')
call f%add('inputs.t', 0.0_rk)
call f%add('inputs.x', [1.0_rk,2.0_rk,3.0_rk])
call f%add('outputs.t', 10.0_rk)
call f%add('outputs.x(1)', 11.0_rk)
call f%add('outputs.x(2)', 22.0_rk)
call f%add('outputs.x(3)', 33.0_rk)

call f%print_file()

call f%destroy()

end program test

As shown, the structure can be built by specifying the variable paths. This way, objects, vectors, vector elements, etc. can all be added. The result of this example is:

{
    "name": "test",
    "inputs": {
        "t": 0.0E+0,
        "x": [
            0.1E+1,
            0.2E+1,
            0.3E+1
        ]
    },
    "outputs": {
        "t": 0.1E+2,
        "x": [
            0.11E+2,
            0.22E+2,
            0.33E+3
        ]
    }
}

So now, in addition to the previous methods of building a JSON structure (reading it from a file, reading it from a string, or building it yourself using pointer variables), there is now another way. Each method has its uses for different applications. Building it from the path strings can be very convenient and also opens up the possibility of easy conversion between a Fortran namelist and a JSON file. I'll show an example of this in a future post. In a previous post, I showed how to do the reverse (JSON to namelist).

JSON-Fortran is my most popular GitHub project (70 stars as of today). It usually makes it to GitHub's monthly "trending" Fortran projects page. I'm always interested to hear about what people are using it for. I added a page on the wiki to list some of the projects that use it, so if you're using it, feel free to add your project to the list.

Binary Search

Binary search is a search algorithm that finds the position of a target value within a sorted array. The following binary search routine is taken from NASTRAN, a venerable finite element analysis program from NASA:

    SUBROUTINE BISLOC (*,ID,ARR,LEN,KN,JLOC)
C-----
C BINARY SEARCH - LOCATE KEY WORD 'ID' IN ARRAY 'ARR', 1ST ENTRY
C IF FOUND, 'JLOC' IS THE MATCHED POSITION IN 'ARR'
C IF NOT FOUND, NON-STANDARD RETURN
C I.E.
C ID = KEY WORD TO MATCH IN ARR. MATCH AGAINST 1ST COL OF ARR
C ARR = ARRAY TO SEARCH. ARR(ROW,COL)
C LEN = LENGTH OF EACH ENTRY IN ARRAY. LEN=ROW
C KN = NUMBER OF ENTRIES IN THE ARR. KN =COL
C JLOC= POINTER RETURNED - FIRST WORD OF ENTRY. MATCHED ROW
C-----
C
    INTEGER ARR(1)
    DATA ISWTCH / 16 /
C
    JJ = LEN - 1
    IF (KN .LT. ISWTCH) GO TO 120
    KLO = 1
    KHI = KN
10  K = (KLO+KHI+1)/2
20  J = K*LEN - JJ
    IF (ID-ARR(J)) 30,90,40
30  KHI = K
    GO TO 50
40  KLO = K
50  IF (KHI-KLO -1) 100,60,10
60  IF (K .EQ. KLO) GO TO 70
    K = KLO
    GO TO 80
70  K = KHI
80  KLO = KHI
    GO TO 20
90  JLOC = J
    RETURN
100 JLOC = KHI*LEN - JJ
    J = KN *LEN - JJ
    IF (ID .GT.ARR(J)) JLOC = JLOC + LEN
110 RETURN 1
C
C SEQUENTIAL SEARCH MORE EFFICIENT
C
120 KHI = KN*LEN - JJ
    DO 130 J = 1,KHI,LEN
    IF (ARR(J)-ID) 130,90,140
130 CONTINUE
    JLOC = KHI + LEN
    GO TO 110
140 JLOC = J
    GO TO 110
    END

As you can see, it is a scene of FORTRAN 66 horrors! However, it can be refactored into a nice modern Fortran routine like so:

pure function bisloc(id,arr) result(jloc)

!! binary search of a sorted array.

implicit none

integer,intent(in) :: id
    !! key word to match in `arr`
integer,dimension(:),intent(in) :: arr
    !! array to search (it is
    !! assumed to be sorted)
integer :: jloc
    !! the first matched index in 'arr'
    !! (if not found, 0 is returned)

integer :: j,k,khi,klo,n
integer,parameter :: iswtch = 16

n = size(arr)
jloc = 0

if ( n<iswtch ) then

    ! sequential search more efficient

    do j = 1 , n
        if ( arr(j)==id ) then
            jloc = j
            return
        else if (arr(j)>id) then
            return ! error
        end if
    end do
    return ! error

else

    klo = 1
    khi = n
    k = (klo+khi+1)/2
    do
        j = k
        if ( id<arr(j) ) then
            khi = k
        else if ( id==arr(j) ) then
            jloc = j
            return
        else
            klo = k
        end if
        if ( khi-klo<1 ) then
            return ! error
        else if ( khi-klo==1 ) then
            if ( k==klo ) then
                k = khi
            else
                k = klo
            end if
            klo = khi
        else
            k = (klo+khi+1)/2
        end if
    end do

end if

end function bisloc

I did change a couple of things:

• The original routine was using an obsolete alternate return (note the * argument) for an error condition. The new one just returns 0 if there is an error.
• The original routine was passing in the array as a vector and treating it like a matrix (it's either searching a row or column of this matrix, I admit I had a hard time telling). The new version assumes the input is a rank-1 array. You can pass in whatever matrix slices you want (say a column: a(:,1) or a row: a(1,:)).
• I also made it a pure function, because that's how I roll.

Note that NASTRAN was released under the NASA Open Source Agreement version 1.3, a somewhat unusual open source license. It isn't considered a "free" license by the FSF since it includes a statement requiring changes to be your "original creation".

Unfortunately, the trend at NASA (and elsewhere) is to declare old Fortran code like this to be totally unmaintainable. So, instead of refactoring them into modern Fortran standards, they are thrown away and rewritten from scratch using a more "modern" language like C++ (whose roots go back to 1972!).

See also

• NASTRAN-95 at NASA's GitHub.

Latest Library Updates

I just released some updates to my two most popular Fortran libraries on GitHub: JSON-Fortran and bspline-fortran. Coincidently, both are now at v5.2.0. Details of the updates are:

JSON-Fortran

There are several new features in this release. The biggest update is that now the code can parse JSON files that include comments (it just ignores them). You can even specify the character that identifies a comment. For example, if using # as a comment character, the following file can now be parsed just fine:

{
    "t": 0.12345,  # this is the time
    "x": 123.7173  # this is the state
}

Technically, comments are not part of the JSON standard. Douglas Crockford, the creator of JSON, had his reasons [1] for not including them, which I admit I don't understand (something about parsing directives and interoperability?) I mainly use JSON for configuration files, where it is nice to have comments. Crockford's suggestion for this use case is to pipe your commented JSON files through something called JSMin before parsing, a solution which seems somewhat ridiculous for Fortran users. So, never fear, now we can have comments in our JSON files and continue not using JavaScript for anything.

Another big change is the addition of support for the RFC 6901 "JSON Pointer" path specification [2]. This can be used to retrieve data from a JSON structure using its path. Formerly, JSON-Fortran used a simple path specification syntax, which broke down if the keys contained special characters such as ( or ). The new way works for all keys.

Bspline-Fortran

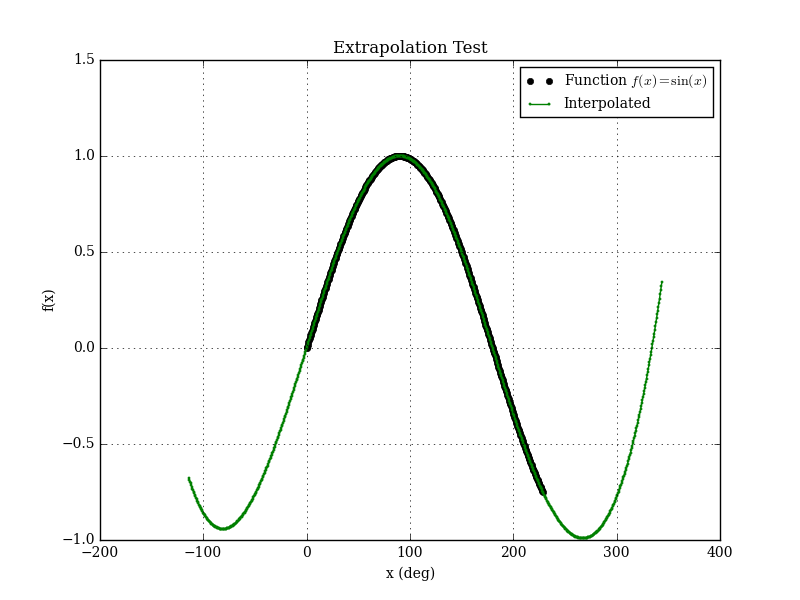
A minor update to Bspline-Fortran is the addition of an extrapolation mode. Formerly, if an interpolation was requested outside the bounds of the data, an error was returned. Now, the user has the option of enabling extrapolation.

See also

1. D. Crockford, "Comments in JSON", Apr 30, 2012 [Google Plus]
2. JavaScript Object Notation (JSON) Pointer, RFC 6901, April 2013 [IETF]

Fortran CSV Module

The lowly CSV (comma-separated values) file never gets any respect. Sure, it isn't really standardized, but it is a very useful text file format for columns of data, and is frequently encountered in science/engineering fields. Of course, there is no good modern Fortran library for reading and writing CSV files (see [1-2] for some older Fortran 90 code for writing only). Searching the internet (e.g., [3-4]) you will find various ad hoc suggestions for handling these files. It's amazing how little Fortran users expect their language to support non-numerical algorithms. No Fortran programmer would ever suggest that someone roll their own matrix inverse routine, but they don't see anything wrong with having to write their own data file parser (if you told a Python user they had to write their own CSV parser, you'd be laughed out of the place).

So, I created fortran-csv-module (now available on GitHub), a modern Fortran library for reading and writing CSV files. Everything is handled by an object-oriented csv_file class. Here is an example for writing a file:

program csv_write_test

use csv_module
use iso_fortran_env, only: wp => real64

implicit none

type(csv_file) :: f
logical :: status_ok

! open the file
call f%open('test.csv',n_cols=4,status_ok=status_ok)

! add header
call f%add(['x','y','z','t'])
call f%next_row()

! add some data:
call f%add([1.0_wp,2.0_wp,3.0_wp],real_fmt='(F5.3)')
call f%add(.true.)
call f%next_row()
call f%add([4.0_wp,5.0_wp,6.0_wp],real_fmt='(F5.3)')
call f%add(.false.)
call f%next_row()

! finished
call f%close(status_ok)

end program csv_write_test

Which produces the following file:

 x,y,z,t 1.000,2.000,3.000,T 4.000,5.000,6.000,F

Real, integer, logical, or character data can be added as scalars, vectors, and matrices.

When reading a CSV file, the data is stored internally in the class as allocatable character strings, which can be retrieved as real, integer, logical or character vectors as necessary. For example, to get the x, y, z, and t vectors from the previously-generated file:

program csv_read_test

use csv_module
use iso_fortran_env, only: wp => real64

implicit none

type(csv_file) :: f
character(len=30),dimension(:),allocatable :: header
real(wp),dimension(:),allocatable :: x,y,z
logical,dimension(:),allocatable :: t
logical :: status_ok
integer,dimension(:),allocatable :: itypes

! read the file
call f%read('test.csv',header_row=1,status_ok=status_ok)

! get the header and type info
call f%get_header(header,status_ok)
call f%variable_types(itypes,status_ok)

! get some data
call f%get(1,x,status_ok)
call f%get(2,y,status_ok)
call f%get(3,z,status_ok)
call f%get(4,t,status_ok)

! destroy the file
call f%destroy()

end program csv_read_test

Various options are user-selectable for specifying the format (e.g., changing the quote or delimiter characters). You can choose to enclose strings (or all fields) in quotes or not. The library works pretty well, and there are probably additional improvements that could be made. For one thing, it doesn't properly handle the case of a string that contains the delimiter character (I'll eventually fix this). If anybody has any other improvements, fork it and send me a pull request. The license is BSD, so you can use it for whatever you want.

See also

1. J. Burkardt, CSV_IO -- Read and Write Comma Separated Values (CSV) Files. [note: it doesn't actually contain any CSV reading capability]
2. A. Markus, FLIBS -- Includes a csv_file module for writing CSV files.
3. How to read a general csv file [Intel Fortran Forum]
4. Read data from a .csv file in fortran [Stack Overflow]

Multidimensional Linear Interpolation (Part 2)

In an earlier post, I mentioned that we needed an object-oriented modern Fortran library for multidimensional linear interpolation. Well, here it is. I call it finterp, and it is available on GitHub. It can be used for 1D-6D interpolation/extrapolation of data on a regular grid (i.e., not scattered). It has a similar object-oriented interface as my bspline-fortran library, with initialize, evaluate, and destroy methods like so:

type(linear_interp_3d) :: interp
call interp%initialize(xvec,yvec,zvec,fmat,iflag)
call interp%evaluate(x,y,z,f)
call interp%destroy()

For example, the low-level 3D interpolation evaluate routine is:

pure subroutine interp_3d(me,x,y,z,fxyz)

implicit none

class(linear_interp_3d),intent(inout) :: me
real(wp),intent(in) :: x
real(wp),intent(in) :: y
real(wp),intent(in) :: z
real(wp),intent(out) :: fxyz !! Interpolated ( f(x,y,z) )

integer,dimension(2) :: ix, iy, iz
real(wp) :: p1, p2, p3
real(wp) :: q1, q2, q3
integer :: mflag
real(wp) :: fx11, fx21, fx12, fx22, fxy1, fxy2

call dintrv(me%x,x,me%ilox,ix(1),ix(2),mflag)
call dintrv(me%y,y,me%iloy,iy(1),iy(2),mflag)
call dintrv(me%z,z,me%iloz,iz(1),iz(2),mflag)

q1 = (x-me%x(ix(1)))/(me%x(ix(2))-me%x(ix(1)))
q2 = (y-me%y(iy(1)))/(me%y(iy(2))-me%y(iy(1)))
q3 = (z-me%z(iz(1)))/(me%z(iz(2))-me%z(iz(1)))
p1 = one-q1
p2 = one-q2
p3 = one-q3

fx11 = p1*me%f(ix(1),iy(1),iz(1)) + q1*me%f(ix(2),iy(1),iz(1))
fx21 = p1*me%f(ix(1),iy(2),iz(1)) + q1*me%f(ix(2),iy(2),iz(1))
fx12 = p1*me%f(ix(1),iy(1),iz(2)) + q1*me%f(ix(2),iy(1),iz(2))
fx22 = p1*me%f(ix(1),iy(2),iz(2)) + q1*me%f(ix(2),iy(2),iz(2))
fxy1 = p2*( fx11 ) + q2*( fx21 )
fxy2 = p2*( fx12 ) + q2*( fx22 )

fxyz = p3*( fxy1 ) + q3*( fxy2 )

end subroutine interp_3d

The finterp library is released under a permissive BSD-3 license. As far as I can tell, it is unique among publicly-available Fortran codes in providing linear interpolation for up to 6D data sets. There used to be a Fortran 77 library called REGRIDPACK for regridding 1D-4D data sets (it had the option to use linear or cubic interpolation independently for each dimension). Written by John C. Adams at the National Center for Atmospheric Research in 1999, it used to be hosted at the UCAR website, but the link is now dead. You can still find it on the internet though, as part of other projects (for example here, where it is being used via a Python wrapper). But the licensing is unclear to me.

The dearth of easy-to-find, easy-to-use, high-quality open source modern Fortran libraries is a big problem for the long-term future of the language. Fortran users don't seem to be as interested in promoting their language as users of some of the newer programming languages are. There is a group of us working to change this, but we've got a long way to go. For example, Julia, a programming language only four years old, already has a ton of libraries, some of which are just wrappers to Fortran 77 code that no one's ever bothered to modernize. They even have a yearly conference. An in depth article about this state of affairs is a post for another day.

References

• G. Hoffmann, Multidimensional Linear Interpolation

Numerical Differentiation

I present the initial release of a new modern Fortran library for computing Jacobian matrices using numerical differentiation. It is called NumDiff and is available on GitHub. The Jacobian is the matrix of partial derivatives of a set of \(m\) functions with respect to \(n\) variables:

Typically, each variable \(x_i\) is perturbed by a value \(h_i\) using forward, backward, or central differences to compute the Jacobian one column at a time (\(\partial \mathbf{f} / \partial x_i\)). Higher-order methods are also possible [1]. The following finite difference formulas are currently available in the library:

• Two points:
  • \((f(x+h)-f(x)) / h\)
  • \((f(x)-f(x-h)) / h\)
• Three points:
  • \((f(x+h)-f(x-h)) / (2h)\)
  • \((-3f(x)+4f(x+h)-f(x+2h)) / (2h)\)
  • \((f(x-2h)-4f(x-h)+3f(x)) / (2h)\)
• Four points:
  • \((-2f(x-h)-3f(x)+6f(x+h)-f(x+2h)) / (6h)\)
  • \((f(x-2h)-6f(x-h)+3f(x)+2f(x+h)) / (6h)\)
  • \((-11f(x)+18f(x+h)-9f(x+2h)+2f(x+3h)) / (6h)\)
  • \((-2f(x-3h)+9f(x-2h)-18f(x-h)+11f(x)) / (6h)\)
• Five points:
  • \((f(x-2h)-8f(x-h)+8f(x+h)-f(x+2h)) / (12h)\)
  • \((-3f(x-h)-10f(x)+18f(x+h)-6f(x+2h)+f(x+3h)) / (12h)\)
  • \((-f(x-3h)+6f(x-2h)-18f(x-h)+10f(x)+3f(x+h)) / (12h)\)
  • \((-25f(x)+48f(x+h)-36f(x+2h)+16f(x+3h)-3f(x+4h)) / (12h)\)
  • \((3f(x-4h)-16f(x-3h)+36f(x-2h)-48f(x-h)+25f(x)) / (12h)\)

The basic features of NumDiff are listed here:

• A variety of finite difference methods are available (and it is easy to add new ones).
• If you want, you can specify a different finite difference method to use to compute each column of the Jacobian.
• You can also specify the number of points of the methods, and a suitable one of that order will be selected on-the-fly so as not to violate the variable bounds.
• I also included an alternate method using Neville's process which computes each element of the Jacobian individually [2]. It takes a very large number of function evaluations but produces the most accurate answer.
• A hash table based caching system is implemented to cache function evaluations to avoid unnecessary function calls if they are not necessary.
• It supports very large sparse systems by compactly storing and computing the Jacobian matrix using the sparsity pattern. Optimization codes such as SNOPT and Ipopt can use this form.
• It can also return the dense (\(m \times n\)) matrix representation of the Jacobian if that sort of thing is your bag (for example, the older SLSQP requires this form).
• It can also return the \(J*v\) product, where \(J\) is the full (\(m \times n\)) Jacobian matrix and v is an (\(n \times 1\)) input vector. This is used for Krylov type algorithms.
• The sparsity pattern can be supplied by the user or computed by the library.
• The sparsity pattern can also be partitioned so as compute multiple columns of the Jacobian simultaneously so as to reduce the number of function calls [3].
• It is written in object-oriented Fortran 2008. All user interaction is through a NumDiff class.
• It is open source with a BSD-3 license.

I haven't yet really tried to fine-tune the code, so I make no claim that it is the most optimal it could be. I'm using various modern Fortran vector and matrix intrinsic routines such as PACK, COUNT, etc. Likely there is room for efficiency improvements. I'd also like to add some parallelization, either using OpenMP or Coarray Fortran. OpenMP seems to have some issues with some modern Fortran constructs so that might be tricky. I keep meaning to do something real with coarrays, so this could be my chance.

So, there you go internet. If anybody else finds it useful, let me know.

References

1. G. Engeln-Müllges, F. Uhlig, Numerical Algorithms with Fortran, Springer-Verlag Berlin Heidelberg, 1996.
2. J. Oliver, "An algorithm for numerical differentiation of a function of one real variable", Journal of Computational and Applied Mathematics 6 (2) (1980) 145–160. [A Fortran 77 implementation of this algorithm by David Kahaner was formerly available from NIST, but the link seems to be dead. My modern Fortran version is available here.]
3. T. F. Coleman, B. S. Garbow, J. J. Moré, "Algorithm 618: FORTRAN subroutines for estimating sparse Jacobian Matrices", ACM Transactions on Mathematical Software (TOMS), Volume 10 Issue 3, Sept. 1984.

GOTO Still Considered Harmful

For a number of years I have been familiar with the observation that the quality of programmers is a decreasing function of the density of go to statements in the programs they produce. -- Edsger W. Dijkstra

One of the classics of computer science is Edsger Dijkstra's "Go To Statement Considered Harmful", written in 1968. This missive argued that the GOTO statement (present in several languages at the time, including Fortran) was too primitive for high-level programming languages, and should be avoided.

Most people now agree with this, although some even today think that GOTOs are fine under some circumstances. They are present in C and C++, and are apparently used extensively in the Linux kernel. A recent study of C code in GitHub concluded that GOTO use is not that bad and is mainly used for error-handling and cleanup tasks, for situations where there are no better alternatives in C. However, C being a low-level language, we should not expect much from it. For modern Fortran users however, there are better ways to do these things. For example, unlike in C, breaking out of multiple loops is possible without GOTOs by using named DO loops with an EXIT statement like so:

a_loop : do a=1,n
    b_loop: do b=1,m
        !do some stuff ...
        if (done) exit a_loop ! break out of the outer loop
        !...
    end do b_loop
end do a_loop

In old-school Fortran (or C) this would be something like this:

do a=1,n
    do b=1,m
        ! do some stuff ...
        if (done) goto 10 ! break out of the outer loop
        ! ...
    end do
end do
10 continue

Of course, these two simple examples are both functionally equivalent, but the first one uses a much more structured approach. It's also a lot easier to follow what is going on. Once a line number is declared, there's nothing to stop a GOTO statement from anywhere in the code from jumping there (see spaghetti code). In my view, it's best to avoid this possibility entirely. In modern Fortran, DO loops (with CYCLE and EXIT), SELECT CASE statements, and other language constructs have obviated the need for GOTO for quite some time. Fortran 2008 added the BLOCK construct which was probably the final nail in the GOTO coffin, since it allows for the most common use cases (exception handing and cleanup) to be easily done without GOTOs. For example, in this code snippet, the main algorithm is contained within a BLOCK, and the exception handling code is outside:

main: block
    ! do some stuff ...
    if (error) exit main ! if there is a problem anywhere in this block,
    ! then exit to the exception handling code.
    ! ...
    return ! if everything is OK, then return
end block main

! exception handling code here

The cleanup case is similar (which is code that is always called):

main: block
    ! do some stuff ...
    if (need_to_cleanup) exit main ! for cleanup
    ! ...
end block main

! cleanup code here

I don't believe any of the new programming languages that have cropped up in the past couple of decades has included a GOTO statement (although someone did create a goto statement for Python as an April Fool's joke in 2004). Of course, the presence of GOTO's doesn't mean the programmer is bad or that the code isn't going to work well. There is a ton of legacy Fortran 77 code out there that is rock solid, but unfortunately littered with GOTOs. An example is the DIVA integrator from the JPL MATH77 library (the screenshot above is from this code). First written in 1987, it is code of the highest quality, and has been used for decades in many spacecraft applications. However, it is also spaghetti code of the highest order, and seems like it would be unimaginably hard to maintain or modify at this point.

See also

• E. W. Dijkstra, "Go To Statement Considered Harmful", Communications of the ACM, Vol. 11, No. 3, March 1968, pp. 147-148 [online version here]
• E. A. Meyer, "Considered Harmful" Essays Considered Harmful, December 28, 2002.
• M. Nagappan, et. al, "An Empirical Study of Goto in C Code from GitHub Repositories", Proceedings of the 2015 10th Joint Meeting on Foundations of Software Engineering, Pages 404-414
• Using GOTO in Linux Kernel Code, January 13, 2003,

Fortran at 60

Today marks the 60th anniversary of the release of the original Fortran Programmer's Reference Manual. Fortran was the world's first high-level computer programming language, was developed beginning in 1953 at IBM by a team lead by John Backus. The first compiler was released in 1957. According to the manual, one of the main features was:

Object programs produced by FORTRAN will be nearly as efficient as those written by good programmers.

The first Fortran compiler (which was also the first optimizing compiler) was named one of the top 10 algorithms of the 20th century:

The creation of Fortran may rank as the single most important event in the history of computer programming: Finally, scientists (and others) could tell the computer what they wanted it to do, without having to descend into the netherworld of machine code. Although modest by modern compiler standards—Fortran I consisted of a mere 23,500 assembly-language instructions—the early compiler was nonetheless capable of surprisingly sophisticated computations. As Backus himself recalls in a recent history of Fortran I, II, and III, published in 1998 in the IEEE Annals of the History of Computing, the compiler "produced code of such efficiency that its output would startle the programmers who studied it."

The entire manual was only 51 pages long. Fortran has evolved significantly since the 1950s, and the descendant of this fairly simple language continues to be used today. The most recent version of the language (a 603 page ISO standard) was published in 2010.

See also

• John W. Backus, New York Times obituary, March 20, 2007.
• J. Backus, "The History of FORTRAN I, II, and III", ACM SIGPLAN Notices - Special issue: History of programming languages conference, Volume 13 Issue 8, August 1978, Pages 165 - 180.

Computing Pi

The digits of \(\pi\) can be computed using the "Spigot algorithm" [1-2]. The interesting thing about this algorithm is that it doesn't use any floating point computations, only integers.

A Fortran version of the algorithm is given below (a translation of the Pascal program in the reference). It computes the first 10,000 digits of \(\pi\). The nines and predigit business is because the algorithm will occasionally output 10 as the next digit, and the 1 will need to be added to the previous digit. If we know in advance that this won't occur for a given range of digits, then the code can be greatly simplified. It can also be reformulated to compute multiple digits at a time if we change the base (see [1] for the simplified version in base 10,000).

subroutine compute_pi()

    implicit none

    integer, parameter :: n = 10000 ! number of digits to compute
    integer, parameter :: len = 10*n/3 + 1

    integer :: i, j, k, q, x, nines, predigit
    integer, dimension(len) :: a

    a = 2
    nines = 0
    predigit = 0

    do j = 1, n
        q = 0
        do i = len, 1, -1
            x = 10*a(i) + q*i
            a(i) = mod(x, 2*i - 1)
            q = x/(2*i - 1)
        end do
        a(1) = mod(q, 10)
        q = q/10
        if (q == 9) then
            nines = nines + 1
        else if (q == 10) then
            write (*, '(I1)', advance='NO') predigit + 1
            do k = 1, nines
                write (*, '(I1)', advance='NO') 0
            end do
            predigit = 0
            nines = 0
        else
            if (j == 2) then
                write (*, '(I1,".")', advance='NO') predigit
            else if (j /= 1) then
                write (*, '(I1)', advance='NO') predigit
            end if
            predigit = q
            if (nines /= 0) then
            do k = 1, nines
                write (*, '(I1)', advance='NO') 9
            end do
            nines = 0
            end if
        end if
    end do
    write (*, '(I1)', advance='NO') predigit

end subroutine compute_pi

The algorithm as originally published contained a mistake (len = 10*n/3). The correction is due to [3]. The code above produces the following output:

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273724587006606315588174881520920962829254091715364367892590360011330530548820466521384146951941511609433057270365759591953092186117381932611793105118548074462379962749567351885752724891227938183011949129833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132000568127145263560827785771342757789609173637178721468440901224953430146549585371050792279689258923542019956112129021960864034418159813629774771309960518707211349999998372978049951059731732816096318595024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303598253490428755468731159562863882353787593751957781857780532171226806613001927876611195909216420198938095257201065485863278865936153381827968230301952035301852968995773622599413891249721775283479131515574857242454150695950829533116861727855889075098381754637464939319255060400927701671139009848824012858361603563707660104710181942955596198946767837449448255379774726847104047534646208046684259069491293313677028989152104752162056966024058038150193511253382430035587640247496473263914199272604269922796782354781636009341721641219924586315030286182974555706749838505494588586926995690927210797509302955321165344987202755960236480665499119881834797753566369807426542527862551818417574672890977772793800081647060016145249192173217214772350141441973568548161361157352552133475741849468438523323907394143334547762416862518983569485562099219222184272550254256887671790494601653466804988627232791786085784383827967976681454100953883786360950680064225125205117392984896084128488626945604241965285022210661186306744278622039194945047123713786960956364371917287467764657573962413890865832645995813390478027590099465764078951269468398352595709825822620522489407726719478268482601476990902640136394437455305068203496252451749399651431429809190659250937221696461515709858387410597885959772975498930161753928468138268683868942774155991855925245953959431049972524680845987273644695848653836736222626099124608051243884390451244136549762780797715691435997700129616089441694868555848406353422072225828488648158456028506016842739452267467678895252138522549954666727823986456596116354886230577456498035593634568174324112515076069479451096596094025228879710893145669136867228748940560101503308617928680920874760917824938589009714909675985261365549781893129784821682998948722658804857564014270477555132379641451523746234364542858444795265867821051141354735739523113427166102135969536231442952484937187110145765403590279934403742007310578539062198387447808478489683321445713868751943506430218453191048481005370614680674919278191197939952061419663428754440643745123718192179998391015919561814675142691239748940907186494231961567945208095146550225231603881930142093762137855956638937787083039069792077346722182562599661501421503068038447734549202605414665925201497442850732518666002132434088190710486331734649651453905796268561005508106658796998163574736384052571459102897064140110971206280439039759515677157700420337869936007230558763176359421873125147120532928191826186125867321579198414848829164470609575270695722091756711672291098169091528017350671274858322287183520935396572512108357915136988209144421006751033467110314126711136990865851639831501970165151168517143765761835155650884909989859982387345528331635507647918535893226185489632132933089857064204675259070915481416549859461637180270981994309924488957571282890592323326097299712084433573265489382391193259746366730583604142813883032038249037589852437441702913276561809377344403070746921120191302033038019762110110044929321516084244485963766983895228684783123552658213144957685726243344189303968642624341077322697802807318915441101044682325271620105265227211166039666557309254711055785376346682065310989652691862056476931257058635662018558100729360659876486117910453348850346113657686753249441668039626579787718556084552965412665408530614344431858676975145661406800700237877659134401712749470420562230538994561314071127000407854733269939081454664645880797270826683063432858785698305235808933065757406795457163775254202114955761581400250126228594130216471550979259230990796547376125517656751357517829666454779174501129961489030463994713296210734043751895735961458901938971311179042978285647503203198691514028708085990480109412147221317947647772622414254854540332157185306142288137585043063321751829798662237172159160771669254748738986654949450114654062843366393790039769265672146385306736096571209180763832716641627488880078692560290228472104031721186082041900042296617119637792133757511495950156604963186294726547364252308177036751590673502350728354056704038674351362222477158915049530984448933309634087807693259939780541934144737744184263129860809988868741326047215695162396586457302163159819319516735381297416772947867242292465436680098067692823828068996400482435403701416314965897940924323789690706977942236250822168895738379862300159377647165122893578601588161755782973523344604281512627203734314653197777416031990665541876397929334419521541341899485444734567383162499341913181480927777103863877343177207545654532207770921201905166096280490926360197598828161332316663652861932668633606273567630354477628035045077723554710585954870279081435624014517180624643626794561275318134078330336254232783944975382437205835311477119926063813346776879695970309833913077109870408591337464144282277263465947047458784778720192771528073176790770715721344473060570073349243693113835049316312840425121925651798069411352801314701304781643788518529092854520116583934196562134914341595625865865570552690496520985803385072242648293972858478316305777756068887644624824685792603953527734803048029005876075825104747091643961362676044925627420420832085661190625454337213153595845068772460290161876679524061634252257719542916299193064553779914037340432875262888963995879475729174642635745525407909145135711136941091193932519107602082520261879853188770584297259167781314969900901921169717372784768472686084900337702424291651300500516832336435038951702989392233451722013812806965011784408745196012122859937162313017114448464090389064495444006198690754851602632750529834918740786680881833851022833450850486082503930213321971551843063545500766828294930413776552793975175461395398468339363830474611996653858153842056853386218672523340283087112328278921250771262946322956398989893582116745627010218356462201349671518819097303811980049734072396103685406643193950979019069963955245300545058068550195673022921913933918568034490398205955100226353536192041994745538593810234395544959778377902374216172711172364343543947822181852862408514006660443325888569867054315470696574745855033232334210730154594051655379068662733379958511562578432298827372319898757141595781119635833005940873068121602876496286744604774649159950549737425626901049037781986835938146574126804925648798556145372347867330390468838343634655379498641927056387293174872332083760112302991136793862708943879936201629515413371424892830722012690147546684765357616477379467520049075715552781965362132392640616013635815590742202020318727760527721900556148425551879253034351398442532234157623361064250639049750086562710953591946589751413103482276930624743536325691607815478181152843667957061108615331504452127473924544945423682886061340841486377670096120715124914043027253860764823634143346235189757664521641376796903149501910857598442391986291642193994907236234646844117394032659184044378051333894525742399508296591228508555821572503107125701266830240292952522011872676756220415420516184163484756516999811614101002996078386909291603028840026910414079288621507842451670908700069928212066041837180653556725253256753286129104248776182582976515795984703562226293486003415872298053498965022629174878820273420922224533985626476691490556284250391275771028402799806636582548892648802545661017296702664076559042909945681506526530537182941270336931378517860904070866711496558343434769338578171138645587367812301458768712660348913909562009939361031029161615288138437909904231747336394804575931493140529763475748119356709110137751721008031559024853090669203767192203322909433467685142214477379393751703443661991040337511173547191855046449026365512816228824462575916333039107225383742182140883508657391771509682887478265699599574490661758344137522397096834080053559849175417381883999446974867626551658276584835884531427756879002909517028352971634456212964043523117600665101241200659755851276178583829204197484423608007193045761893234922927965019875187212726750798125547095890455635792122103334669749923563025494780249011419521238281530911407907386025152274299581807247162591668545133312394804947079119153267343028244186041426363954800044800267049624820179289647669758318327131425170296923488962766844032326092752496035799646925650493681836090032380929345958897069536534940603402166544375589004563288225054525564056448246515187547119621844396582533754388569094113031509526179378002974120766514793942590298969594699556576121865619673378623625612521632086286922210327488921865436480229678070576561514463204692790682120738837781423356282360896320806822246801224826117718589638140918390367367222088832151375560037279839400415297002878307667094447456013455641725437090697939612257142989467154357846878861444581231459357198492252847160504922124247014121478057345510500801908699603302763478708108175450119307141223390866393833952942578690507643100638351983438934159613185434754649556978103829309716465143840700707360411237359984345225161050702705623526601276484830840761183013052793205427462865403603674532865105706587488225698157936789766974220575059683440869735020141020672358502007245225632651341055924019027421624843914035998953539459094407046912091409387001264560016237428802109276457931065792295524988727584610126483699989225695968815920560010165525637567

See also

1. S. Rabinowitz, Abstract 863–11–482: A Spigot Algorithm for Pi, American Mathematical Society, 12(1991)30, 1991.
2. S. Rabinowitz, S. Wagon, "A Spigot Algorithm for the Digits of \(\pi\)", American Mathematical Monthly, Vol. 102, Issue 3, March 1995, p. 195-203.
3. J. Arndt, C. Haenel, π Unleashed, Springer, 2000.

Backward Compatibility

"Perfection is achieved, not when there is nothing more to add, but when there is nothing left to take away." -- Antoine de Saint-Exupéry

The Fortran standards committee generally refuses to break backward compatibility when Fortran is updated. This is a good thing (take that, Python), and code written decades ago can still be compiled fine today. However, over the years, various old features of the language have been identified as "obsolescent", namely:

• Alternate return
• Assumed-length character functions
• CHARACTER*(*) form of CHARACTER declaration
• Computed GO TO statement
• DATA statements among executable statements
• Fixed source form
• Statement functions
• ENTRY statement
• Labeled DO loops [will be obsolescent in Fortran 2015]
• EQUIVALENCE [will be obsolescent in Fortran 2015]
• COMMON Blocks [will be obsolescent in Fortran 2015]
• BLOCK DATA [will be obsolescent in Fortran 2015]

And a small set of features has actually been deleted from the language standard:

• ASSIGN and assigned GO TO statements
• Assigned FORMAT specifier
• Branching to an END IF statement from outside its IF block
• H edit descriptor
• PAUSE statement
• Real and double precision DO control variables and DO loop control expressions
• Arithmetic IF [will be deleted in Fortran 2015]
• Shared DO termination and termination on a statement other than END DO or CONTINUE [will be deleted in Fortran 2015]

In practice, all compilers still support all the old features (although special compiler flags may be necessary to use them). Normally, you shouldn't use any of this junk in new code. But there is still a lot of legacy FORTRAN 77 code out there that people want (or need) to compile. However, as I've shown many times in this blog, updating old Fortran code to modern standards is not really that big of a deal.

When the next revision of the language (Fortran 2015) is published, it will mark the first time since Fortran was first standardized in 1966 that we will have two consecutive minor revisions of the language (2008 was also a minor revision). The last major revision of the language was Fortran 2003 over a decade ago. There still is no feature-complete free Fortran 2003 compiler (although gfortran currently does include almost all of the Fortran 2003 standard).

Personally, I would tend to prefer a faster-paced cycle of Fortran language development. I'm not one of those who think the language should include regular expressions or a 2D graphics API (seriously, C++?). But, there are clearly potentially useful things that are missing. I think the standard should finally acknowledge the existence of the file system, and provide intrinsic routines for changing and creating directories, searching for files, etc. Currently, if you want to do anything like that you have to resort to system calls or non-standard extensions provided by your compiler vender (thus making the code less portable). A much more significant upgrade would be better support for generic programming (maybe we'll get that in Fortran 2025). There are also many other feature proposals out there (see references below).

See also

• Fortran Feature Proposals – at the Fortran Wiki.
• E. Myklebust, Feature Proposals for Fortran – The Complete Set, ISO/IEC JTC1/SC22/WG5 N1972
• C. Page, "Suggestion: Improved String-handling in Fortran", October 1, 2015.
• V. Snyder, "Units of Measure in Fortran", N1970, April 22, 2013.
• S. Lionel, "The Future of Fortran", March 27, 2015