Sep 11, 2016
Decently syntax highlighted Fortran code on the internet is hard to come by. None of the major sites where people are likely to visit to learn about Fortran have it:
- The Google Groups hosting of comp.lang.fortran (I don't really expect much from this one since it's just Usenet.)
- Stack Overflow (we should expect better from them, since they have had syntax highlighting for many other languages for years.) It looks like they are using Google's code-prettify (which seems to have a pull request ready to provide syntax highlighting for Fortran, so perhaps there is hope?)
- Intel Fortran compiler documentation [example] (people pay good money for this compiler, and so should ask for better documentation).
- GFortran documentation (their entire Fortran website looks like it is from the late 1990s, and could certainly use an overhaul).
Luckily GitHub has syntax highlighting for Fortran, as well as the Fortran Wiki.
Personally, I hate looking at non-syntax highlighted code. It's not aesthetically pleasing and I find it hard to read. On this blog, I'm using a Fortran plugin for SyntaxHighlighter Evolved, which I downloaded somewhere at some point and have modified to account for various newer Fortran language features. It's not perfect, but it looks pretty good.
Consider this example from the gfortran website:
Now that looks just awful, and not just because they are using ancient syntax such as (/, /), and .eq.. Whereas the following syntax-highlighted one looks great:
program test_all
implicit none
logical :: l
l = all([.true., .true., .true.])
write(*,*) l
call section()
contains
subroutine section()
integer,dimension(2,3) :: a, b
a = 1
b = 1
b(2,2) = 2
write(*,*) all(a == b, 1)
write(*,*) all(a == b, 2)
end subroutine section
end program test_all
FORD-produced documentation has nice syntax highlighting for Fortran code provided by Pygments (which is written in Python). An example can be found here. Rouge is another code highlighter (written in Ruby) that supports Fortran and can output as HTML. Both Pygments and Rouge are open source and released under permissive licenses.
Sep 10, 2016
Intel has announced the availability of version 17.0 of the Intel Fortran Compiler (part of Intel Parallel Studio XE 2017). Slowly but surely, the compiler is approaching full support for the current Fortran 2008 standard. New Fortran 2008 features added in this release are:
TYPE(intrinsic-type)- Pointer initialization
- Implied-shape
PARAMETER arrays
- Extend
EXIT statement to all valid construct names
- Support
BIND(C) in internal procedures
In addition, the compiler now also supports the standard auto-reallocation on assignment by default (previously, you had to use a special compiler flag to enable this behavior).
See also
Aug 27, 2016
JSON-Fortran 5.1 is out. There are several new features in this release. I added a get_path() routine that can be used to return the path of a variable in a JSON structure. This can be used along with the traverse() routine to do something pseudointeresting: convert a JSON file into a Fortran namelist file. Why would anyone want to do that, you ask? Who knows. Consider the following example:
program why
use json_module
implicit none
type(json_core) :: json
type(json_value), pointer :: p
integer :: iunit !! file unit
open (newunit=iunit, file='data.nml', status='REPLACE')
write (iunit, '(A)') '&DATA'
call json%initialize()
call json%parse(file='data.json', p=p)
call json%traverse(p, print_json_variable)
write (iunit, '(A)') '/'
close (iunit)
contains
subroutine print_json_variable(json, p, finished)
!! A `traverse` routine for printing out all
!! the variables in a JSON structure.
implicit none
class(json_core), intent(inout) :: json
type(json_value), pointer, intent(in) :: p
logical(json_LK), intent(out) :: finished
character(kind=json_CK, len=:), allocatable :: path
character(kind=json_CK, len=:), allocatable :: value
logical(json_LK) :: found
type(json_value), pointer :: child
integer(json_IK) :: var_type
call json%get_child(p, child)
finished = .false.
!only print the leafs:
if (.not. associated(child)) then
!fortran-style:
call json%get_path(p, path, found, &
use_alt_array_tokens=.true., &
path_sep=json_CK_'%')
if (found) then
call json%info(p, var_type=var_type)
select case (var_type)
case (json_array, json_object)
!an empty array or object
!don't print anything
return
case (json_string)
! note: strings are returned escaped
! without quotes
call json%get(p, value)
value = '"'//value//'"'
case default
! get the value as a string
! [assumes strict_type_checking=false]
call json%get(p, value)
end select
!check for errors:
if (json%failed()) then
finished = .true.
else
write (iunit, '(A)') &
path//json_CK_' = '//value//','
end if
else
finished = .true.
end if
end if
end subroutine print_json_variable
end program why
Here, we are simply traversing the entire JSON structure, and printing out the paths of the leaf nodes using a namelist-style syntax. For the example JSON file:
{
"t": 0.0,
"x": [1.0, 2.0, 3.0],
"m": 2000.0,
"name": "foo"
}
This program will produce the following namelist file:
&DATA
t = 0.0E+0,
x(1) = 0.1E+1,
x(2) = 0.2E+1,
x(3) = 0.3E+1,
m = 0.2E+4,
name = "foo",
/
Which could be read using the following Fortran program:
program namelist_test
use iso_fortran_env, only: wp => real64
implicit none
real(wp) :: t,m,x(3)
integer :: iunit,istat
character(len=10) :: name
! define the namelist:
namelist /DATA/ t,x,m,name
! read the namelist:
open(newunit=iunit,file='data.nml',status='OLD')
read(unit=iunit,nml=DATA,iostat=istat)
close(unit=iunit)
end program namelist_test
There is also a new minification option for printing a JSON structure with no extra whitespace. For example:
{"t":0.0E+0,"x":[0.1E+1,0.2E+1,0.3E+1],"m":0.2E+4,"name":"foo"}
See also
- f90nml -- A Python module for parsing Fortran namelist files
Aug 07, 2016
Often the need arises to add (or subtract) elements from an array on the fly. Fortran 2008 allows for this to be easily done using standard allocatable arrays. An example for integer arrays is shown here:
integer,dimension(:),allocatable :: x
x = [1,2,3]
x = [x,[4,5,6]] ! x is now [1,2,3,4,5,6]
x = x(1:4) ! x is now [1,2,3,4]
Note that, if using the Intel compiler, this behavior is not enabled by default for computational efficiency reasons. To enable it you have to use the -assume realloc_lhs compiler flag.
Resizing an array like this carries a performance penalty. When adding a new element, the compiler will likely have to make a temporary copy of the array, deallocate the original and resize it, and then copy over the original elements and the new one. A simple test case is shown here (compiled with gfortran 6.1.0 with -O3 optimization enabled):
program test
implicit none
integer,dimension(:),allocatable :: x
integer :: i
x = [0]
do i=1,100000
x = [x,i]
end do
end program test
This requires 2.828986 seconds on my laptop (or 35,348 assignments per second). Now, that may be good enough for some applications. However, performance can be improved significantly by allocating the array in chunks, as shown in the following example, where we allocate in chunks of 100 elements, and then resize it to the correct size at the end:
program test
implicit none
integer, dimension(:), allocatable :: x
integer :: i, n
integer, parameter :: chunk_size = 100
n = 0
do i = 0, 100000
call add_to(x, i, n, chunk_size, finished=i == 100000)
end do
contains
pure subroutine add_to(vec, val, n, chunk_size, finished)
implicit none
integer, dimension(:), allocatable, intent(inout) :: vec
!! the vector to add to
integer, intent(in) :: val
!! the value to add
integer, intent(inout) :: n
!! counter for last element added to vec.
!! must be initialized to size(vec)
!! (or 0 if not allocated) before first call
integer, intent(in) :: chunk_size
!! allocate vec in blocks of this size (>0)
logical, intent(in) :: finished
!! set to true to return vec
!! as its correct size (n)
integer, dimension(:), allocatable :: tmp
if (allocated(vec)) then
if (n == size(vec)) then
! have to add another chunk:
allocate (tmp(size(vec) + chunk_size))
tmp(1:size(vec)) = vec
call move_alloc(tmp, vec)
end if
n = n + 1
else
! the first element:
allocate (vec(chunk_size))
n = 1
end if
vec(n) = val
if (finished) then
! set vec to actual size (n):
if (allocated(tmp)) deallocate (tmp)
allocate (tmp(n))
tmp = vec(1:n)
call move_alloc(tmp, vec)
end if
end subroutine add_to
end program test
This requires only 0.022938 seconds (or 4,359,577 assignments per second) which is nearly 123 times faster. Note that we are using the Fortran 2003 move_alloc intrinsic function, which saves us an extra copy operation when the array is resized.
Increasing the chunk size can improve performance even more:
Depending on the specific application, a linked list is another option for dynamically-sized objects.
May 30, 2016
Sorting is one of the fundamental problems in computer science, so of course Fortran does not include any intrinsic sorting routine (we've got Bessel functions, though!) String sorting is a special case of this problem which includes various choices to consider, for example:
- Natural or ASCII sorting
- Case sensitive (e.g., 'A'<'a') or case insensitive (e.g., 'A'=='a')
"Natural" sorting (also called "alphanumeric sorting" means to take into account numeric values in the string, rather than just comparing the ASCII value of each of the characters. This can produce an order that looks more natural to a human for strings that contain numbers. For example, in a "natural" sort, the string "case2.txt" will come before "case100.txt", since the number 2 comes before the number 100. For example, natural sorting is the method used to sort file names in the MacOS X Finder (see image at right). While, interestingly, an ls -l from a Terminal merely does a basic ASCII sort.
For string sorting routines written in modern Fortran, check out my GitHub project stringsort. This library contains routines for both natural and ASCII string sorting. Natural sorting is achieved by breaking up each string into chunks. A chunk consists of a non-numeric character or a contiguous block of integer characters. A case insensitive search is done by simply converting each character to lowercase before comparing them. I make no claim that the routines are particularly optimized. One limitation is that contiguous integer characters are stored as an integer(INT32) value, which has a maximum value of 2147483647. Although note that it is easy to change the code to use integer(INT64) variables to increase this range up to 9223372036854775807 if necessary. Eliminating integer size restrictions entirely is left as an exercise for the reader.
Consider the following test case:
character(len=*),dimension(6) :: &
str = [ 'z1.txt ', &
'z102.txt', &
'Z101.txt', &
'z100.txt', &
'z10.txt ', &
'Z11.txt ' ]
This list can be sorted (at least) four different ways:
Case Insensitive
ASCII
z1.txt
z10.txt
z100.txt
Z101.txt
z102.txt
Z11.txt
natural
z1.txt
z10.txt
Z11.txt
z100.txt
Z101.txt
z102.txt
Case Sensitive
ASCII
Z101.txt
Z11.txt
z1.txt
z10.txt
z100.txt
z102.txt
natural
Z11.txt
Z101.txt
z1.txt
z10.txt
z100.txt
z102.txt
Each of these can be done using stringsort with the following subroutine calls:
call lexical_sort_recursive(str,case_sensitive=.false.)
call lexical_sort_natural_recursive(str,case_sensitive=.false.)
call lexical_sort_recursive(str,case_sensitive=.true.)
call lexical_sort_natural_recursive(str,case_sensitive=.true.)
Original Quicksort algorithm by Tony Hoare, 1961 (Communications of the ACM)
The routines use the quicksort algorithm, which was originally created for sorting strings (specifically words in Russian sentences so they could be looked up in a Russian-English dictionary). The algorithm is easily implemented in modern Fortran using recursion (non-recursive versions were also available before recursion was added to the language in Fortran 90). Quicksort was named one of the top 10 algorithms of the 20th century by the ACM (Fortran was also on the list).
See also
May 15, 2016
Asteroid Redirect Mission [NASA]
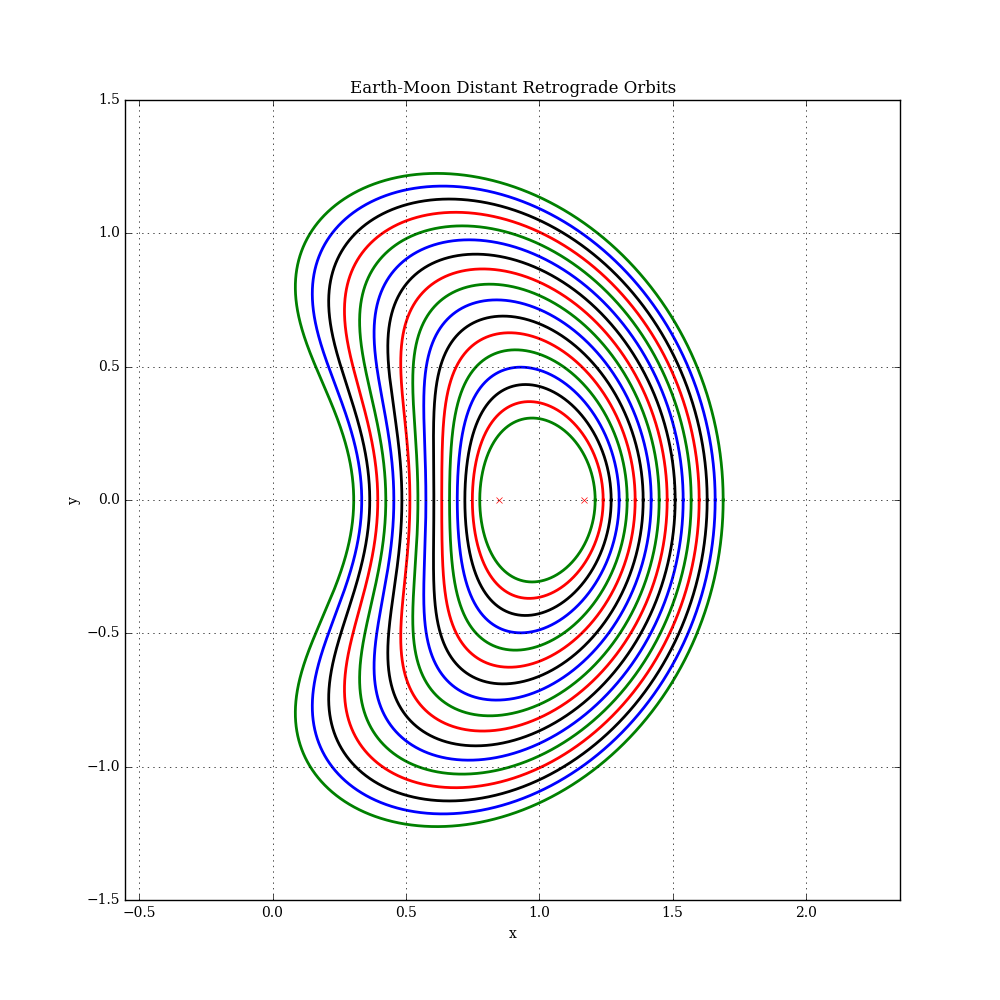
A "distant-retrograde orbit" (DRO) is a periodic orbit in the circular restricted three-body problem (CR3BP) that, in the rotating frame, looks like a large quasi-elliptical retrograde orbit around the secondary body. Moon-centered DRO's in the Earth-Moon system were considered as a possible destination for depositing a captured asteroid for NASA's proposed Asteroid Redirect Mission, since they can remain stable for long periods of time (decades or even centuries).
DROs can be computed using components from the Fortran Astrodynamics Toolkit. All we need is:
- A numerical integrator (we will use an 8th order Runge-Kutta method from Shanks [4]).
- The equations of motion for the circular restricted three-body problem (CR3BP).
- A nonlinear equation solver (we will use HYBRD1 from MINPACK).
We will use the canonical normalized CR3BP reference frame where the distance between the primary and secondary body is normalized to one. The initial state is placed on the x-axis, at a specified distance from the Moon. The y-velocity \(v_y\) is allowed to vary, and \(v_x=0\). The problem can be solved with two optimization variables:
- The time of flight for one orbit period (i.e., the duration between two consecutive x-axis crossings on the \(x>1\) side)
- The initial y-velocity component
and two constraints:
- \(y=0\) at the final time
- \(v_x=0\) at the final time (i.e., a perpendicular crossing of the x-axis)
The problem can be simplified to one variable and one constraint by using an integrator with an event-finding capability so that the integration proceeds until the x-axis crossing occurs (eliminating the time of flight and the \(y=0\) constraint from the optimization problem). That is how we will proceed here, since the Runge-Kutta module we are using does include an event location capability.
The code for computing a single Earth-Moon DRO is shown here:
program dro_test
use fortran_astrodynamics_toolkit
implicit none
real(wp), parameter :: mu_earth = 398600.436233_wp
!! km^3/s^2
real(wp), parameter :: mu_moon = 4902.800076_wp
!! km^3/s^2
integer, parameter :: n = 6
!! number of state variables
real(wp), parameter :: t0 = 0.0_wp
!! initial time (normalized)
real(wp), parameter :: tmax = 1000.0_wp
!! max final time (normalized)
real(wp), parameter :: dt = 0.001_wp
!! time step (normalized)
real(wp), parameter :: xtol = 1.0e-4_wp
!! tolerance for hybrd1
integer, parameter :: maxfev = 1000
!! max number of function evaluations for hybrd1
real(wp), dimension(n), parameter :: x0 = &
[1.2_wp, &
0.0_wp, &
0.0_wp, &
0.0_wp, &
-0.7_wp, &
0.0_wp]
!! initial guess for DRO state (normalized)
real(wp), dimension(1) :: vy0
!! initial y velocity (xvec for hybrd1)
real(wp), dimension(1) :: vxf
!! final x velocity (fvec for hybrd1)
real(wp) :: mu
!! CRTPB parameter
type(rk8_10_class) :: prop
!! integrator
integer :: info
!! hybrd1 status flag
! compute the CRTBP parameter & Jacobi constant:
mu = compute_crtpb_parameter(mu_earth, mu_moon)
! initialize integrator:
call prop%initialize(n, func, g=x_axis_crossing)
! now, solve for DRO:
vy0 = x0(5) ! initial guess
call hybrd1(dro_fcn, 1, vy0, vxf, tol=xtol, info=info)
! solution:
write (*, *) ' info=', info
write (*, *) ' vy0=', vy0
write (*, *) ' vxf=', vxf
contains
!**************************************
subroutine dro_fcn(n, xvec, fvec, iflag)
!! DRO function for hybrd1
implicit none
integer, intent(in) :: n !! `n=1` in this case
real(wp), dimension(n), intent(in) :: xvec !! `vy0`
real(wp), dimension(n), intent(out) :: fvec !! `vxf`
integer, intent(inout) :: iflag !! not used here
real(wp) :: gf, t0, tf_actual
real(wp), dimension(6) :: x, xf
real(wp), parameter :: tol = 1.0e-8_wp
!! event finding tolerance
t0 = zero ! epoch doesn't matter for crtbp
x = x0 ! initial guess state
x(5) = xvec(1) ! vy0 (only optimization variable)
!integrate to the next x-axis crossing:
call prop%integrate_to_event(t0, x, dt, tmax, tol, tf_actual, xf, gf)
!want x-velocity at the x-axis crossing to be zero:
fvec = xf(4)
end subroutine dro_fcn
!**************************************
subroutine func(me, t, x, xdot)
!! CRTBP derivative function
implicit none
class(rk_class), intent(inout) :: me
real(wp), intent(in) :: t
real(wp), dimension(me%n), intent(in) :: x
real(wp), dimension(me%n), intent(out) :: xdot
call crtbp_derivs(mu, x, xdot)
end subroutine func
!**************************************
subroutine x_axis_crossing(me, t, x, g)
!! x-axis crossing event function
implicit none
class(rk_class), intent(inout) :: me
real(wp), intent(in) :: t
real(wp), dimension(me%n), intent(in) :: x
real(wp), intent(out) :: g
g = x(2) ! y = 0 at x-axis crossing
end subroutine x_axis_crossing
end program dro_test
Trajectory plots for some example solutions are shown below (each with a different x component). The L1 and L2 libration points are also shown. In this plot, the Earth is at the origin and the Moon is at [x=1,y=0]. See this example for more details.
References
- The Restricted Three-Body Problem - MIT OpenCourseWare, S. Widnall 16.07 Dynamics Fall 2008, Version 1.0.
- C. A. Ocampo, G. W. Rosborough, "Transfer trajectories for distant retrograde orbiters of the Earth", AIAA Spaceflight Mechanics Meeting, Pasadena, CA, Feb. 22-24, 1993.
- Asteroid Redirect Mission and Human Space Flight, June 19, 2013.
- E. B. Shanks, "Higher Order Approximations of Runge-Kutta Type", NASA Technical Note, NASA TN D-2920, Sept. 1965.
- Henon, M., "Numerical Exploration of the Restricted Problem. V. Hill's Case: Periodic Orbits and Their Stability," Astronomy and Astrophys. Vol 1, 223-238, 1969.
May 15, 2016
The SLATEC Common Mathematical Library (CML) is written in FORTRAN 77 and contains over 1400 general purpose mathematical and statistical routines. SLATEC is an acronym for the "Sandia, Los Alamos, Air Force Weapons Laboratory Technical Exchange Committee", an organization formed in 1974 by the computer centers of these organizations. In 1977, it was decided to build a FORTRAN library to provide portable, non-proprietary, mathematical software for member sites' supercomputers. Version 1.0 of the CML was released in April 1982.
An example SLATEC routine is shown below, which computes the inverse hyperbolic cosine:
*DECK ACOSH
FUNCTION ACOSH (X)
C***BEGIN PROLOGUE ACOSH
C***PURPOSE Compute the arc hyperbolic cosine.
C***LIBRARY SLATEC (FNLIB)
C***CATEGORY C4C
C***TYPE SINGLE PRECISION (ACOSH-S, DACOSH-D, CACOSH-C)
C***KEYWORDS ACOSH, ARC HYPERBOLIC COSINE, ELEMENTARY FUNCTIONS, FNLIB,
C INVERSE HYPERBOLIC COSINE
C***AUTHOR Fullerton, W., (LANL)
C***DESCRIPTION
C
C ACOSH(X) computes the arc hyperbolic cosine of X.
C
C***REFERENCES (NONE)
C***ROUTINES CALLED R1MACH, XERMSG
C***REVISION HISTORY (YYMMDD)
C 770401 DATE WRITTEN
C 890531 Changed all specific intrinsics to generic. (WRB)
C 890531 REVISION DATE from Version 3.2
C 891214 Prologue converted to Version 4.0 format. (BAB)
C 900315 CALLs to XERROR changed to CALLs to XERMSG. (THJ)
C 900326 Removed duplicate information from DESCRIPTION section.
C (WRB)
C***END PROLOGUE ACOSH
SAVE ALN2,XMAX
DATA ALN2 / 0.6931471805 5994530942E0/
DATA XMAX /0./
C***FIRST EXECUTABLE STATEMENT ACOSH
IF (XMAX.EQ.0.) XMAX = 1.0/SQRT(R1MACH(3))
C
IF (X .LT. 1.0) CALL XERMSG ('SLATEC', 'ACOSH', 'X LESS THAN 1',
+ 1, 2)
C
IF (X.LT.XMAX) ACOSH = LOG (X + SQRT(X*X-1.0))
IF (X.GE.XMAX) ACOSH = ALN2 + LOG(X)
C
RETURN
END
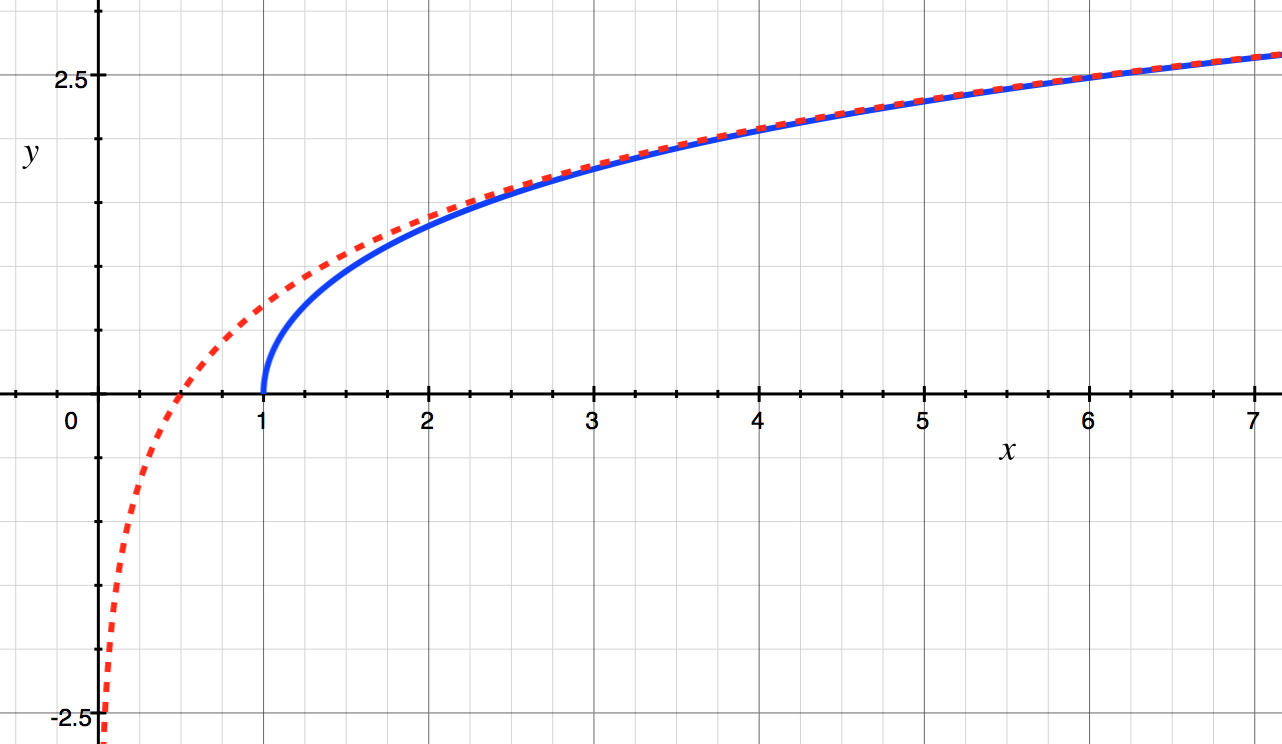
Of course, this routine is full of nonsense from the point of view of a modern Fortran programmer (fixed-form source, implicitly typed variables, SAVE and DATA statements, constants computed at run time rather than compile time, hard-coding of the numeric value of ln(2), etc.). And you don't even want to know what's happening in the R1MACH() function. A modern version would look something like this:
pure elemental function acosh(x) result(acoshx)
!! arc hyperbolic cosine
use iso_fortran_env, only: wp => real64
implicit none
real(wp),intent(in) :: x
real(wp) :: acoshx
real(wp),parameter :: aln2 = &
log(2.0_wp)
real(wp),parameter :: r1mach3 = &
real(radix(1.0_wp),wp)**(-digits(1.0_wp)) !! largest relative spacing
real(wp),parameter :: xmax = &
1.0_wp/sqrt(r1mach3)
if ( x<1.0_wp ) then
error stop 'slatec : acosh : x less than 1'
else
if ( x<xmax ) then
acoshx = log(x + sqrt(x*x - 1.0_wp))
else
acoshx = aln2 + log(x)
end if
end if
end function acosh
Of course, the point is moot, since ACOSH() is now an intrinsic function in Fortran 2008, so we don't need either of these anymore. Unfortunately, like many great Fortran codes, SLATEC has been frozen in amber since the early 1990's. It does contain a great many gems, however, and any deficiencies in the original Fortran 77 code can be easily remedied using modern Fortran standards. See also, for example, my own DDEABM project, which is a complete refactoring and upgrade of the Adams-Bashforth-Moulton ODE solver from SLATEC.
The GNU Scientific Library was started in 1996 to be a "modern version of SLATEC". Of course, rather than refactoring into modern Fortran (Fortran 90 had been published several years earlier, but I believe it was some time before a free compiler was available) they decided to start over in C. There's now even a Fortran interface to GSL (so now we can use a Fortran wrapper to call a C function that replaced a Fortran function that worked perfectly well to begin with!) The original SLATEC was a public domain work of the US government, and so can be used without restrictions in free or proprietary applications, but GSL is of course, GPL, so you're out of luck if you are unable to accept the ~~restrictions~~ (I mean freedom) of that license.
Note that John Burkardt has produced a version of SLATEC translated to free-form source. The license for this modified version is unclear. Many of his other codes are LGPL (still more restrictive than the original public domain codes). It's not a full refactoring, either. The codes still contain non-standard extensions and obsolescent and now-unnecessary features such as COMMON blocks. What we really need is a full modern refactoring of SLATEC (and other unmaintained codes like the NIST CMLIB and NSWC, etc.)
References
- Fong, Kirby W., Jefferson, Thomas H., Suyehiro, Tokihiko, Walton, Lee, "Guide to the SLATEC Common Mathematical Library", July 1993.
- SLATEC source code at Netlib.
May 09, 2016
JSON-Fortran 5.0 is out. This release finally brings thread-safety to the library. Note that it does break backward compatibility with previous versions, but hopefully it isn't too much trouble to modify your code to be compatible with the new release. I've provided a short guide describing what you need to do.
JSON-Fortran is a Fortran 2008 JSON API, based on an earlier project called FSON (which was written in Fortran 95). FSON was not thread-safe, and so neither was JSON-Fortran at first. This was mainly due to the use of various global settings, and global variables used during parsing and for keeping track of errors.
In the transition from FSON to JSON-Fortran, I added a high-level json_file class that is used to do a lot of common operations (e.g. open a JSON file and read data from it). However, building a JSON structure from scratch is done using lower-level json_value pointers. In the 5.0 release, there is a new factory class called json_core that is now the interface for manipulating json_value variables. Thus, each instance of this class can exist independently of any others (each with potentially different settings), and so provides thread-safe operation and error handling. The json_file class simply contains an instance of json_core, which contains all the variables and settings that were formerly global to the entire module.
A very simple example of the pre-5.0 usage would be:
program test
use json_module
implicit none
type(json_file) :: json
integer :: ival
character(len=:),allocatable :: cval
logical :: found
call json_initialize()
call json%load_file(filename='myfile.json')
call json%print_file() !print to the console
call json%get('var.i',ival,found)
call json%get('var.c',cval,found)
call json%destroy()
end program test
For 5.0, all you have to do is change:
to
and you're done. All global variables have been eliminated and the only entities that are user-accessible are three public types and their methods.
There are also a ton of other new features in JSON-Fortran 5.0, including new APIs, such as:
json_core%validate() -- test the validity of a JSON structure (i.e., a json_value linked list).json_core%is_child_of() -- test if one json_value is a child of another.json_core%swap() -- swap two json_value elements in a JSON structure (this may be useful for sorting purposes).json_core%rename() -- rename a json_value variable in a JSON structure.
And new settings (set during the call to initialize()) such as:
- Trailing spaces can now be significant for name comparisons.
- Name comparisons can now be case sensitive or case insensitive.
- Can enable strict type checking to avoid automatic conversion of numeric data (say, integer to double) when getting data from a JSON structure.
- Can set the number of spaces for indenting when writing JSON data to a file.
See also
Apr 28, 2016
Gfortran 6.1 (part of GCC) has been released. The release notes don't say much with respect to Fortran:
- The
MATMUL intrinsic is now inlined for straightforward cases if front-end optimization is active. The maximum size for inlining can be set to n with the -finline-matmul-limit=n option and turned off with -finline-matmul-llimit=0.
- The
-Wconversion-extra option will warn about REAL constants which have excess precision for their kind.
- The
-Winteger-division option has been added, which warns about divisions of integer constants which are truncated. This option is included in -Wall by default.
But, apparently, this version includes some nice updates, including support for Fortran 2008 submodules, Fortran 2015 Coarray events, as well as bug fixes for deferred-length character variables.
See also
Apr 24, 2016
Here's another example using the C interoperability features of modern Fortran. First introduced in Fortran 2003, this allows for easily calling C routines from Fortran (and vice versa) in a standard and portable way. Further interoperability features will also be added in the next edition of the standard.
For a Fortran user, strings in C are pretty awful (like most things in C). This example shows how to call a C function that returns a string (in this case, the dlerror function).
module get_error_module
use, intrinsic :: iso_c_binding
implicit none
private
public :: get_error
interface
!interfaces to C functions
function dlerror() result(error) &
bind(C, name='dlerror')
import
type(c_ptr) :: error
end function dlerror
function strlen(str) result(isize) &
bind(C, name='strlen')
import
type(c_ptr),value :: str
integer(c_int) :: isize
end function strlen
end interface
contains
function get_error() result(error_message)
!! wrapper to C function char *dlerror(void);
character(len=:),allocatable :: error_message
type(c_ptr) :: cstr
integer(c_int) :: n
cstr = dlerror() ! pointer to C string
if (c_associated(cstr)) then
n = strlen(cstr) ! get string length
block
!convert the C string to a Fortran string
character(kind=c_char,len=n+1),pointer :: s
call c_f_pointer(cptr=cstr,fptr=s)
error_message = s(1:n)
nullify(s)
end block
else
error_message = ''
end if
end function get_error
end module get_error_module
First we define the bindings to two C routines so that we can call them from Fortran. This is done using the INTERFACE block. The main one is the dlerror function itself, and we will also use the C strlen function for getting the length of a C string. The bind(C) attribute indicates that they are C functions. The get_error function first calls dlerror, which returns a variable of type(c_ptr), which is a C pointer. We use c_f_pointer to cast the C pointer into a Fortran character string (a CHARACTER pointer variable with the same length). Note that, after we know the string length, the block construct allows us to declare a new variable s of the length we need (this is a Fortran 2008 feature). Then we can use it like any other Fortran string (in this case, we assign it to error_message, the deferred-length string returned by the function).
Of course, Fortran strings are way easier to deal with, especially deferred-length (allocatable) strings, and don't require screwing around with pointers or '\0' characters. A few examples are given below:
subroutine string_examples()
implicit none
!declare some strings:
character(len=:),allocatable :: s1,s2
!string assignment:
s1 = 'hello world' !set the string value
s2 = s1 !set one string equal to another
!string slice:
s1 = s1(1:5) !now, s1 is 'hello'
!string concatenation:
s2 = s1//' '//s1 ! now, s2 is 'hello hello'
!string length:
write(*,*) len(s2) ! print length of s2 (which is now 11)
!and there are no memory leaks,
!since the allocatables are automatically
!deallocated when they go out of scope.
end subroutine string_examples
See also
