Dec 28, 2015

DDEABM is variable step size, variable order Adams-Bashforth-Moulton PECE solver for integrating a system of first order ordinary differential equations [1-2]. It is a public-domain code originally developed in the 1970s-1980s, written in FORTRAN 77, and is available from Netlib (as part of the SLATEC Common Mathematical Library). DDEABM is primarily designed to solve non-stiff and mildly-stiff differential equations when derivative evaluations are expensive, high accuracy results are needed or answers at many specific points are required. It is based on the earlier ODE/STEP/INTRP codes described in [3-4].
DDEABM is a great code, but like many of the greats of Fortran, it seems to have been frozen in amber for 30 years. There are a couple of translations into other programming languages out there such as IDL and Matlab. It is also the ancestor of the Matlab ode113 solver (indeed, they were both written by the same person [5]). But, it looks like poor Fortran users have been satisfied with using it as is, in all its FORTRAN 77 glory.
So, I've taken the code and significantly refactored it to bring it up to date to modern standards (Fortran 2003/2008). This is more than just a conversion from fixed to free-form source. The updated version is now object-oriented and thread-safe, and also has a new event finding capability (there is a version of this code that had root-finding capability, but it seems to be based on an earlier version of the code, and also has some limitations such as a specified maximum number of equations). The new event finding feature incorporates the well-known ZEROIN algorithm [6-7] for finding a root on a bracketed interval. Everything is wrapped up in an easy-to-use class, and it also supports the exporting of intermediate integration points.
The new code is available on GitHub and is released under a permissive BSD-style license. It is hoped that it will be useful. There are some other great ODE codes that could use the same treatment (e.g. DLSODE/DVODE from ODEPACK, DIVA from MATH77, and DOP853 from Ernst Hairer).
References
- L. F. Shampine, H. A. Watts, "DEPAC - Design of a user oriented package of ode solvers", Report SAND79-2374, Sandia Laboratories, 1979.
- H. A. Watts, "A smoother interpolant for DE/STEP, INTRP and DEABM: II", Report SAND84-0293, Sandia Laboratories, 1984.
- L. F. Shampine, M. K. Gordon, "Solving ordinary differential equations with ODE, STEP, and INTRP", Report SLA-73-1060, Sandia Laboratories, 1973.
- L. F. Shampine, M. K. Gordon, "Computer solution of ordinary differential equations, the initial value problem", W. H. Freeman and Company, 1975.
- L. F. Shampine and M. W. Reichelt, "The MATLAB ODE Suite" [MathWorks].
- R. P. Brent, "An algorithm with guaranteed convergence for finding a zero of a function", The Computer Journal, Vol 14, No. 4., 1971.
- R. P. Brent, "Algorithms for minimization without derivatives", Prentice-Hall, Inc., 1973.
Nov 13, 2015

Good news everyone! The US government just announced that it has reached an agreement with NVIDIA to produce an open source Fortran front-end for the LLVM compiler infrastructure. It will be based on the existing commercial Portland Group compiler (NVIDIA purchased the Portland Group a couple of years ago). Source code for the Fortran front-end is expected to be available in late 2016. From the announcement:
The project is being spearheaded by the Lawrence Livermore, Sandia and Los Alamos national laboratories in response to the need for a robust open-source Fortran solution to complement and support the burgeoning use of LLVM and the CLANG C++ compiler in the HPC community. Large HPC applications, such as those developed by the NNSA Laboratories, are often built on mixed-language modules, and require a common compiler infrastructure that supports both C/C++ and Fortran. Fortran also remains widely used in the broader scientific computing community, supporting simulation science to advance national security, medicine, energy, climate and basic science missions.
Does Fortran support for LLVM mean that we'll eventually be able to have Fortran code running on our iPads? Only time will tell...
See also
Nov 06, 2015
My bspline-fortran multidimensional interpolation library is now at version 4.0. The documentation can be found here. Since I first mentioned it here, I've made many updates to this library, including:
- Added object-oriented wrappers to the core routines. The user now has the choice to use the older subroutine interface or the new object-oriented interface.
- Added a set of 1D routines (suggested by a user on GitHub). The library now works for 1D-6D data sets.
- Everything is now thread-safe for your multithreaded pleasure.
The new object-oriented interface makes it pretty easy to use from modern Fortran. The classes have only three methods (initialize, evaluate, and destroy). For example, a 3D case would look like this:
type(bspline_3d) :: s
call s%initialize(x,y,z,fcn,kx,ky,kz,iflag)
call s%evaluate(xval,yval,zval,idx,idy,idz,f,iflag)
call s%destroy()
The core routines of bspline-fortran were written in the early 1980s. Good Fortran code can live on for decades after it is written. While this is great, it also means that there is a lot of old Fortran code out there that is written in a coding style that no modern programmer should accept. This can be OK for well documented library routines that the user never needs to change (see, for example SPICE or LAPACK). However, refactoring old code using modern concepts can provide many advantages, as is demonstrated in this case.
See also
- DBSPLIN and DTENSBS from the NIST Core Math Library.
- Carl de Boor, A Practical Guide to Splines, Springer-Verlag, New York, 1978.
Oct 17, 2015
Fortran's TRANSFER function (introduced in Fortran 95) is a somewhat strange function that can be used to do some interesting things not otherwise possible in earlier versions of the language. In fact, it can be used to achieve a sort of poor-man's polymorphism. It can also still be useful in modern Fortran.
All this function does is transfers the bitwise representation of one variable into another variable. This is different from casting a variable of one type to another. For example:
program transfer_example
use iso_fortran_env
integer(int64) :: i
real(real64) :: d
i = 1
d = i !d is 1.0000000000000000
d = transfer(i,d) !d is 4.9406564584124654E-324
end program transfer_example
The following example shows how to use TRANSFER to create a hash function that can operate on any variable or derived type. The dummy argument of the hash_anything function is an unlimited polymorphic variable (class(*)). The bitwise representation of this variable is then transferred into a character string big enough to hold it (making use of the Fortran 2008 STORAGE_SIZE intrinsic), which can then be hashed using any hash function that takes a character string as an input (a basic DJB method is used here).
module hash_module
!integer kind to use for the hash:
use iso_fortran_env, only: ip => INT32
implicit none
contains
function hash_anything(v) result(hash)
!! Hash anything, using unlimited
!! polymorphic variable and transfer()
class(*),intent(in) :: v
integer(ip) :: hash
!!a default character string
!!with the same size as v:
character(len=ceiling(dble(storage_size(v))/&
dble(storage_size(' ')))) :: str
str = transfer(v,str) !transfer bits of v into
!string of the same size
hash = djb_hash(str) !hash it
end function hash_anything
function djb_hash(str) result(hash)
!! Character string hashing with
!! the DJB algorithm. From [1].
character(len=*),intent(in) :: str
integer(ip) :: hash
integer :: i
hash = 5381_ip
do i=1,len(str)
hash = (ishft(hash,5_ip) + hash) + &
ichar(str(i:i))
end do
end function djb_hash
end module hash_module
See also
- Fortran hashing algorithm, July 6, 2013 [Fortran Dev]
- Hash table example [Fortran Wiki]
Aug 27, 2015
Hey, there's an article on the internet that mentions Coarray Fortran (introduced in the Fortran 2008 standard), and how it is the right tool for a particular massive computational job. It doesn't mention punchcards, the 1950s, or express any surprise that people are still using Fortran in modern times. Progress?
Excerpt:
Applications such as ECMWF's IFS model use OpenMP (a standard for shared memory parallelization) for computations on the nodes and MPI for communications across the nodes. Generally, this arrangement works well for many applications, but for high-resolution weather modeling using the spectral transform method, it can bog down the application, wasting precious runtime—it simply does not easily allow for any overlap of computation and communication. The use of coarrays (also called PGAS, for Partitioned Global Address Space) in Fortran, however, allows a simple syntax for data to be communicated between tasks at the same time computations are being performed.
See also
Aug 25, 2015

Intel just announced the availability of version 16.0 of the Intel Fortran Compiler (part of Intel Parallel Studio XE 2016). New features include:
- Submodules (Fortran 2008)
IMPURE ELEMENTAL (Fortran 2008)EXIT from BLOCK (Fortran 2008)- Full "Further Interoperability with C" implementation from TS29113 (Fortran 2015)
- Improved coarray performance on Linux and Windows
- On Windows, support for Visual Studio 2015
The new "C Descriptor" feature from Fortran 2015 looks pretty awesome, and finally plugs some of the holes in the C interoperability feature first introduced in Fortran 2003. It now allows C code to interact with Fortran pointers, allocatable variables, assumed shape variables, and CHARACTER(*) strings.
I used to be excited about submodules, which have the potential to reduce compilation cascades for very large projects. However, since Intel added the multi-processor compile option on Windows a few versions ago, that has been less bothersome for me. I'll probably try it out anyway, since it also might be useful for organizational purposes (splitting up very large modules into multiple submodules).
See also
- Intel Fortran Compiler 16.0 Release Notes
- What’s New in Intel Fortran 16.0
Aug 05, 2015

The 4.2.0 release of the JSON-Fortran library is now available on GitHub. This version has a few new features and a couple of minor bug fixes. The source code documentation is also now produced by FORD, which is a great new tool for modern Fortran documentation. It has been out for less than a year and is already far better than other tools that have been around for years. See an example of the output here.
Jul 17, 2015

It looks like JPL just opensourced their MATH77 Fortran library. MATH77 is a library of Fortran 77 subroutines implementing various numerical algorithms. It was developed over decades at JPL, and contains some very high-quality and time-tested code. The code is released under a BSD-type license. There is also a C version for people who love semicolons.
See also
- "MATH77/mathc90 Libraries Available at netlib", July 17, 2015. [comp.lang.fortran]
Jun 30, 2015

Good news for starving students: Intel just announced that their compilers (including the Intel Fortran compiler) are now available under a free, non-commercial license for qualified students on Linux, MacOS X and Windows.
Jun 21, 2015
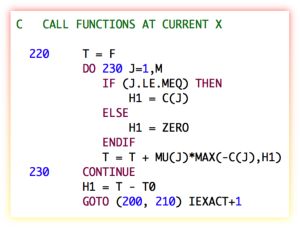
SLSQP [1-2] is a sequential least squares constrained optimization algorithm written by Dieter Kraft in the 1980s. Today, it forms part of the Python pyOpt package for solving nonlinear constrained optimization problems. It was written in FORTRAN 77, and is filled with such ancient horrors like arithmetic IF statements, GOTO statements (even computed and assigned GOTO statements), statement functions, etc. It also assumes the implicit saving of variables in the LINMIN subroutine (which is totally non-standard, but was done by some early compilers), and in some instances assumes that variables are initialized with a zero value (also non-standard, but also done by some compilers). It has an old-fashioned "reverse communication" style interface, with generous use of "WORK" arrays passed around using assumed-size dummy arguments. The pyOpt users don't seem to mind all this, since they are calling it from a Python wrapper, and I guess it works fine (for now).
I don't know if anyone has ever tried to refactor this into modern Fortran with a good object-oriented interface. It seems like it would be a good idea. I've been toying with it for a while. It is always an interesting process to refactor old Fortran code. The fixed-form to free-form conversion can usually be done fairly easily with an automated script, but untangling the spaghetti can be a bit harder. Consider the following code snipet from the subroutine HFTI:
C DETERMINE PSEUDORANK
DO 90 j=1,ldiag
90 IF(ABS(a(j,j)).LE.tau) GOTO 100
k=ldiag
GOTO 110
100 k=j-1
110 kp1=k+1
A modern version that performs the exact same calculation is:
!determine pseudorank:
do j=1,ldiag
if (abs(a(j,j))<=tau) exit
end do
k=j-1
kp1=j
As you can see, no line numbers or GOTO statements are required. The new version even eliminates one assignment and one addition operation. Note that the refactored version depends on the fact that the index of the DO loop, if it completes the loop (i.e., if the exit statement is not triggered), will have a value of ldiag+1. This behavior has been part of the Fortran standard for some time (perhaps it was not when this routine was written?).
There is also a C translation of SLSQP available, which fixes some of the issues in the original code. Their version of the above code snippet is a pretty straightforward translation of the FORTRAN 77 version, except with all the ugliness of C on full display (a[j + j * a_dim1], seriously?):
/* DETERMINE PSEUDORANK */
i__2 = ldiag;
for (j = 1; j <= i__2; ++j) {
/* L90: */
if ((d__1 = a[j + j * a_dim1], fabs(d__1)) <= *tau) {
goto L100;
}
}
k = ldiag;
goto L110;
L100:
k = j - 1;
L110:
kp1 = k + 1;
See Also
- Dieter Kraft, "A Software Package for Sequential Quadratic Programming", DFVLR-FB 88-28, 1988.
- Dieter Kraft, "Algorithm 733: TOMP–Fortran Modules for Optimal Control Calculations," ACM Transactions on Mathematical Software, Vol. 20, No. 3, p. 262-281 (1994).
- John Burkardt, LAWSON Least Squares Routines, 21 October 2008. [Fortran 90 versions of the least squares routines used in SLSQP].






