May 17, 2015
Topological sorting can be used to determine the order in which a collection of interdependent tasks must be performed. For example, when building a complex modern Fortran application, there can be many modules with complex interdependencies (via use association). A Fortran building system (like FoBiS, Foray, or SCons) will perform a topological sort to determine the correct compilation order. In graph theory, the collection of tasks are vertices of a directed graph. If there are no circular dependencies, then it is a directed acyclic graph (DAG).
An example modern Fortran implementation of a topological sorting algorithm is given here. The only public class is dag, which is used to define the graph and perform the sort. The toposort method performs a "depth-first" traversal of the graph using the recursive subroutine dfs. Each vertex is only visited once, and so the algorithm runs in linear time. The routine also triggers an error message for circular dependencies.
module toposort_module
!! Topological sorting, using a recursive
!! depth-first method. The vertices are
!! integer values from (1, 2, ..., nvertices)
implicit none
private
type :: vertex
!! a vertex of a directed acyclic graph (DAG)
integer,dimension(:),allocatable :: edges
integer :: ivertex = 0 !vertex number
logical :: checking = .false.
logical :: marked = .false.
contains
procedure :: set_edges
end type vertex
type,public :: dag
!! a directed acyclic graph (DAG)
type(vertex),dimension(:),allocatable :: vertices
contains
procedure :: set_vertices => dag_set_vertices
procedure :: set_edges => dag_set_edges
procedure :: toposort => dag_toposort
end type dag
contains
subroutine set_edges(me,edges)
!! specify the edge indices for this vertex
implicit none
class(vertex),intent(inout) :: me
integer,dimension(:),intent(in) :: edges
allocate(me%edges(size(edges)))
me%edges = edges
end subroutine set_edges
subroutine dag_set_vertices(me,nvertices)
!! set the number of vertices in the dag
implicit none
class(dag),intent(inout) :: me
integer,intent(in) :: nvertices !! number of vertices
integer :: i
allocate(me%vertices(nvertices))
me%vertices%ivertex = [(i,i=1,nvertices)]
end subroutine dag_set_vertices
subroutine dag_set_edges(me,ivertex,edges)
!! set the edges for a vertex in a dag
implicit none
class(dag),intent(inout) :: me
integer,intent(in) :: ivertex !! vertex number
integer,dimension(:),intent(in) :: edges
call me%vertices(ivertex)%set_edges(edges)
end subroutine dag_set_edges
subroutine dag_toposort(me,order)
!! main toposort routine
implicit none
class(dag),intent(inout) :: me
integer,dimension(:),allocatable,intent(out) :: order
integer :: i,n,iorder
n = size(me%vertices)
allocate(order(n))
iorder = 0 ! index in order array
do i=1,n
if (.not. me%vertices(i)%marked) &
call dfs(me%vertices(i))
end do
contains
recursive subroutine dfs(v)
!! depth-first graph traversal
type(vertex),intent(inout) :: v
integer :: j
if (v%checking) then
error stop 'Error: circular dependency.'
else
if (.not. v%marked) then
v%checking = .true.
if (allocated(v%edges)) then
do j=1,size(v%edges)
call dfs(me%vertices(v%edges(j)))
end do
end if
v%checking = .false.
v%marked = .true.
iorder = iorder + 1
order(iorder) = v%ivertex
end if
end if
end subroutine dfs
end subroutine dag_toposort
end module toposort_module
An example use of this module is given below. Here, we define a graph with five vertices: task 2 depends on 1, task 3 depends on both 1 and 5, and task 4 depends on 5.
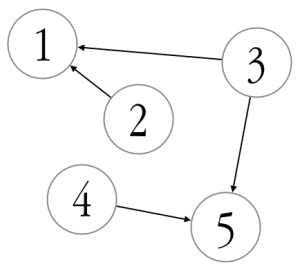
program main
use toposort_module
implicit none
type(dag) :: d
integer,dimension(:),allocatable :: order
call d%set_vertices(5)
call d%set_edges(2,[1]) ! 2 depends on 1
call d%set_edges(3,[5,1]) ! 3 depends on 5 and 1
call d%set_edges(4,[5]) ! 4 depends on 5
call d%toposort(order)
write(*,*) order
end program main
The result is:
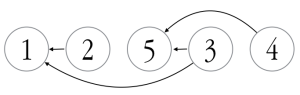
Which is the evaluation order. As far as I can find, the above code is the only modern Fortran topological sorting implementation available on the internet. There is a FORTRAN 77 subroutine here, and a Fortran 90-ish one here (however, neither of them check for circular dependencies).
See also
- Topological Sorting [Everything Under The Sun], June 26, 2013.
- Topological sorting [Wikipedia]
- tsort -- UNIX command for performing topological sorting. [Note that this gives the result in the reverse order from the code listed above.]
May 16, 2015

Part of the confusion about modern Fortran is what file extension to use. This confusion has its roots in the Fortran 90 standard (ISO/IEC 1539:1991) and the introduction of "free-form" source (the older FORTRAN 77 punched-card style was renamed "fixed-form" at this time). Unfortunately, compiler vendors began to use the extension .f90 for free-form files (common fixed-form extensions were .f or .for). Of course, the Fortran standard says nothing about file extensions. This is just one of those things the Lords of Fortran pretend are not important, like the ability to access the command line (not standardized until Fortran 2008) or the file system (still waiting for this). So, that left the compiler vendors (and users) free to do what they wanted, and all of them used .f90 for the new file type.
This was fine until the Fortran 95 standard came along (ISO/IEC 1539-1:1997). Fortran 95 was a minor update to the language (mostly cleaning up some of the half-baked bits of Fortran 90, but also adding some new stuff). This is when things started to go wrong. Since Fortran 90 used the .f90 extension, Fortran 95 should use .f95, right? And then Fortran 2003 came along, and then Fortran 2008, etc. The end result is a confusion of file extensions for free-form source such as .f90, .f95, .f03, .f08, and soon .f15. However, it doesn't make any sense to use the file extension to indicate the Fortran standard. Fortran has a high degree of backward compatibility (Python users take note). So, for example, almost all of Fortran 95 code is valid Fortran 90 code. Even a good deal of FORTRAN 77 code is still perfectly valid Fortran 2008 code. In fact, fixed-form source is still valid even in the Fortran 2008 standard (although only a lunatic would write object-oriented code in fixed-form format).
To sum up: .f90 means free-form source, not Fortran 90, and it's the only extension you should to be using. Stop the madness, or we're really going to be in trouble 75 years from now.
See also
- Steve Lionel, Source Form Just Wants to be Free [Intel.com] January 11, 2013.
Apr 25, 2015

The GNU Project just announced the availability of GCC 5.1. There are various new GFortran features, including:
- Availability of the intrinsic IEEE modules (
ieee_features, ieee_exceptions and ieee_arithmetic) from Fortran 2003.
- Support for
implicit none (external, type) from Fortran 2015.
GFortran is still not completely Fortran 2003 compatible, however.
In Intel news, Intel Parallel Studio XE 2016 is now in beta (which includes v16 of the Intel Fortran Compiler). The major new features are:
- Submodules from Fortran 2008!
impure elemental from Fortran 2008.- "Further Interoperability with C" features from TS29113 (Fortran 2015 draft).
Apr 18, 2015
Python's matplotlib.pyplot is a very nice collection of functions that provide an easy Matlab-like interface for data plotting. It can be used to generate quite professional looking plots. There is a lot of information on the internet about calling Fortran from Python, but what if all you want to do is generate some plots from your (modern) Fortran program? With this in mind, I've created a very simple Fortran wrapper for Pyplot, allowing you to make pretty good plots by writing only Fortran code. Consider the following example:
program test
use,intrinsic :: iso_fortran_env, only: wp => real64
use pyplot_module
implicit none
real(wp),dimension(100) :: x,sx,cx,tx
type(pyplot) :: plt
integer :: i
!generate some data:
x = [(real(i,wp), i=0,size(x)-1)]/5.0_wp
sx = sin(x)
cx = cos(x)
tx = sx * cx
!plot it:
call plt%initialize(grid=.true.,xlabel='angle (rad)',&
title='python_plot test',legend=.true.)
call plt%add_plot(x,sx,label='\$\sin (x)\$',&
linestyle='b-o',markersize=5,linewidth=2)
call plt%add_plot(x,cx,label='\$\cos (x)\$',&
linestyle='r-o',markersize=5,linewidth=2)
call plt%add_plot(x,tx,label='\$\sin (x) \cos (x)\$',&
linestyle='g-o',markersize=2,linewidth=1)
call plt%savefig('test.png')
end program test
The main user interface is the pyplot class, which has methods such as initialize, add_plot, and savefig. This example produces the following plot:
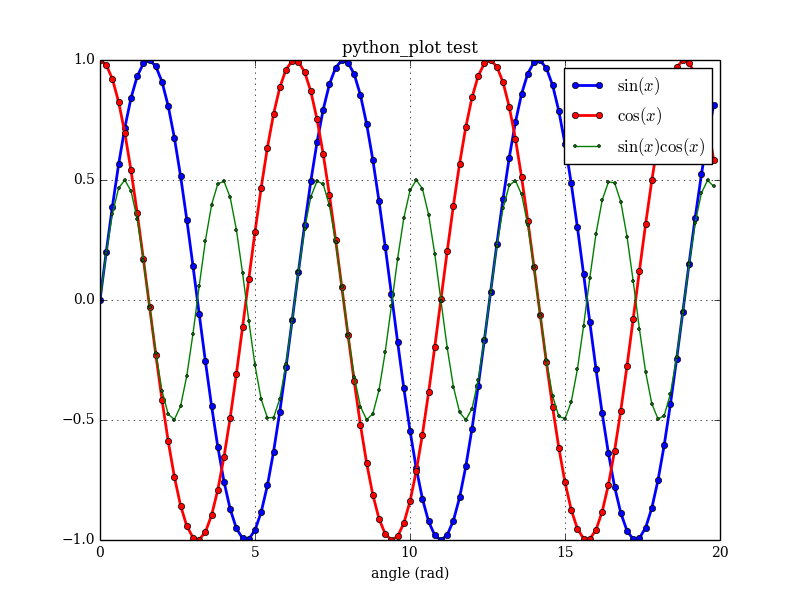
All the module does is generate a Python script, and then runs it and saves the result. The Python call is completely transparent to the Fortran user.
I posted the project to GitHub (pyplot-fortran). Maybe someone else will find it useful, or help to expand it.
See also
- matplotlib
- F2PY Users Guide and Reference Manual --Fortran to Python interface generator
Apr 11, 2015
A simple Fortran implementation of interpolation by Lagrange polynomials is given below. Though named after Joseph-Louis Lagrange, the formula was first discovered by English mathematician Edward Waring.
subroutine lagrange_interpolation(xx,yy,x,y)
!
! Interpolate xx=[x1,x2,...xn]
! yy=[f(x1),f(x2),...,f(xn)]
! Using Lagrange polynomial P(x)
! Returns y = P(x)
!
use,intrinsic :: iso_fortran_env, wp => real64
implicit none
real(wp),dimension(:),intent(in) :: xx
real(wp),dimension(:),intent(in) :: yy
real(wp),intent(in) :: x
real(wp),intent(out) :: y
!local variables:
integer :: j,k,n,m
real(wp) :: p
!check number of points:
n = size(xx)
m = size(yy)
if (n/=m) error stop &
'Error: vectors must be the same size.'
!sum each of the Pj(x) terms:
y = 0.0_wp
do j=1,n
!compute Pj(x):
p = yy(j)
do k=1,n
if (k/=j) p = p * (x-xx(k)) / (xx(j)-xx(k))
end do
y = y + p
end do
end subroutine lagrange_interpolation
Examples of interpolating polynomials for the \(\sin(x)\) function are shown here for different numbers of points \(x=[0.0, 0.01]\), \(x=[0.0, 0.01, 0.02]\), etc.
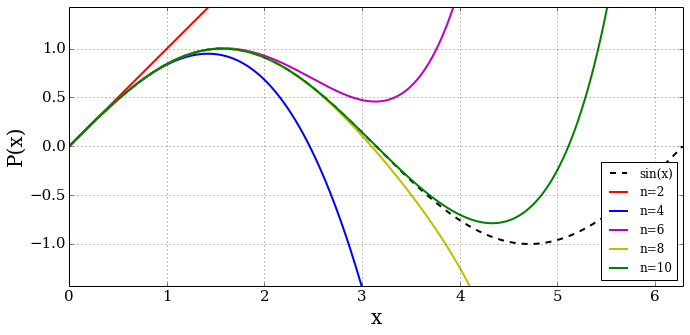
References
Mar 21, 2015

There is a lot of confusion and misinformation about the Fortran programming language on the internet, and a general ignorance about it among programmers. Most younger programmers who use languages invented five minutes ago probably have never seen it, and may only be dimly aware of it as some obsolete language that nobody uses anymore.
You may be surprised to learn that Fortran is a modern, object-oriented, general-purpose programming language. Fortran is not a programming language created by computer scientists to write operating systems, nor does it include every single programming concept anyone's ever heard of. It is a language designed for computational efficiency and efficient array manipulation, and has a clear uncluttered syntax that can be read and understood by non-experts with only a little effort and training. It is particularly suited for numerical and scientific programming by non-expert programmers such as engineers and scientists. Learning all of Fortran is considerably easier than learning all of C++ (as an example). Sure, you can't do template metaprogramming, but few engineer/scientist types would ever want to do that anyway (besides, it's bad for you and could make you go blind).
By "Fortran", I mean modern Fortran (i.e., Fortran 2003 and 2008, which is the latest standard). Yes, the roots of Fortran go way back to the 1950s. Sure, early Fortran programs were written on punched cards. So what? Latin was once scratched into wax tablets, but that isn't really relevant to modern Italian and French speakers. In fact, the Fortran language has evolved considerably since it was first standardized in 1966. It generally has followed a cycle where a major update is followed by a minor update (1977=minor, 1990=major, 1995=minor, 2003=major, 2008=minor). It has been said that the 2003 update was as big an update to Fortran 95 as C++ was to C! Ten years later, the GNU Fortran compiler is still not fully F2003 compliment (the Intel compiler only recently became so).
People who attempt to enter the world of Fortran programming are easily corrupted and discouraged by misinformation. Even a lot of old-school Fortran users are unaware of the later standards. This is too bad, because modern Fortran is actually quite a respectable programming language for a lot of technical applications. This article is a pretty good overview of Fortran for C/C++ programmers. However, it is outdated, since it is confined to Fortran 95. Most of the limitations it mentions (no procedure pointers, clunky character strings, lack of an intent attribute for pointer dummy arguments, the nonstandardness of the ; character) have been rectified in subsequent standards.
The fact is the internet is not really the best source of information for modern Fortran. One day, maybe, there will be vibrant community of Fortran users on the internet, extensive online documentation, open source projects, and all your questions will simply be a web search away (cf., Python). But for now, you'll probably have to buy some books. If a book has the numbers 77, 90, or 95 in the title, don't open it, it will only confuse you. This is not to say that there aren't friendly Fortran folk on the internet who will also help you out. Two of the best places to go with questions are the Intel Fortran forum and the comp.lang.fortran newsgroup (yes, apparently, Usenet still exists).
References
- N. Maclaren, Why (and Why Not) to Use Fortran: Instead of C++, Matlab, Python etc., University of Cambridge Computing Service, June 2012.
- L. Phillips, Scientific computing’s future: Can any coding language top a 1950s behemoth?, May 7, 2014 [arstechnica.com]
- Fortran Wiki -- an open venue for discussing all aspects of the Fortran programming language and scientific computing.
- A. Koenig, C Traps and Pitfalls, AT&T Bell Laboratories.
- Why C and C++ are Awful Programming Languages
Mar 21, 2015
Conversion Factors
- 1 lbm = 0.45359237 kg
- 1 lbf = 4.4482216152605 N
- 1 ft = 0.3048 m
- 1 mile = 1.609344 km
- 1 nmi = 1.852 km
- 1 slug = 1 \(\mathrm{lbf} ~ \mathrm{s}^2 / \mathrm{ft} \approx\) 14.5939029 kg
References
Fortran Code
module conversion_factors
use, intrinsic :: iso_fortran_env, only: wp => real64 !double precision
implicit none
real(wp),parameter :: one = 1.0_wp
real(wp),parameter :: lbm2kg = 0.45359237_wp ! exact
real(wp),parameter :: lbf2N = 4.4482216152605_wp !
real(wp),parameter :: ft2m = 0.3048_wp !
real(wp),parameter :: mile2km = 1.609344_wp !
real(wp),parameter :: nmi2km = 1.852_wp !
real(wp),parameter :: slug2kg = lbf2N/ft2m ! ~ 14.593902937206362
real(wp),parameter :: kg2lbm = one/lbm2kg ! ~ 2.2046226218487757
real(wp),parameter :: N2lbf = one/lbf2N ! ~ 0.2248089430997105
real(wp),parameter :: m2ft = one/ft2m ! ~ 3.280839895013123
real(wp),parameter :: km2mile = one/mile2km ! ~ 0.621371192237334
real(wp),parameter :: km2nmi = one/nmi2km ! ~ 0.5399568034557235
real(wp),parameter :: kg2slug = one/slug2kg ! ~ 0.06852176585679176
end module conversion_factors
Mar 16, 2015

I just tagged the 4.0.0 release of json-fortran. This is the first release with Unicode support (thanks to Izaak Beekman). Who says there are no good open source Fortran projects on the internet?
The Unicode build of the library is optional (and only enabled using the preprocessor directive USE_UCS4). Currently, this only works with Gfortran. It doesn't yet work with the Intel Fortran Compiler, which is lagging behind on Unicode support. The Fortran standard supports Unicode via the selected_char_kind function, which can be used to specify the character set used for a character string, like so:
integer,parameter :: u = selected_char_kind('ISO_10646')
character(kind=u,len=11) :: string = u_'Hello World'
Mar 14, 2015
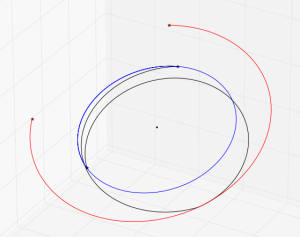
*Earth-Mars Free Return*
Let's try using the Fortran Astrodynamics Toolkit and Pikaia to solve a real-world orbital mechanics problem. In this case, computing the optimal Earth-Mars free return trajectory in the year 2018. This is a trajectory that departs Earth, and then with no subsequent maneuvers, flies by Mars and returns to Earth. The building blocks we need to do this are:
- An ephemeris of the Earth and Mars [DE405]
- A Lambert solver [1]
- Some equations for hyperbolic orbits [given below]
- An optimizer [Pikaia]
The \(\mathbf{v}_{\infty}\) vector of a hyperbolic planetary flyby (using patched conic assumptions) is simply the difference between the spacecraft's heliocentric velocity and the planet's velocity:
- \(\mathbf{v}_{\infty} = \mathbf{v}_{heliocentric} - \mathbf{v}_{planet}\)
The hyperbolic turning angle \(\Delta\) is the angle between \(\mathbf{v}_{\infty}^{-}\) (the \(\mathbf{v}_{\infty}\) before the flyby) and the \(\mathbf{v}_{\infty}^{+}\) (the \(\mathbf{v}_{\infty}\) vector after the flyby). The turning angle can be used to compute the flyby periapsis radius \(r_p\) using the equations:
- \(e = \frac{1}{\sin(\Delta/2)}\)
- \(r_p = \frac{\mu}{v_{\infty}^2}(e-1)\)
So, from the Lambert solver, we can obtain Earth to Mars, and Mars to Earth trajectories (and the heliocentric velocities at each end). These are used to compute the \(\mathbf{v}_{\infty}\) vectors at: Earth departure, Mars flyby (both incoming and outgoing vectors), and Earth return.
There are three optimization variables:
- The epoch of Earth departure [modified Julian date]
- The outbound flight time from Earth to Mars [days]
- The return flyby time from Mars to Earth [days]
There are also two constraints on the heliocentric velocity vectors before and after the flyby at Mars:
- The Mars flyby must be unpowered (i.e., no propulsive maneuver is performed). This means that the magnitude of the incoming (\(\mathbf{v}_{\infty}^-\)) and outgoing (\(\mathbf{v}_{\infty}^+\)) vectors must be equal.
- The periapsis flyby radius (\(r_p\)) must be greater than some minimum value (say, 160 km above the Martian surface).
For the objective function (the quantity that is being minimized), we will use the sum of the Earth departure and return \(\mathbf{v}_{\infty}\) vector magnitudes. To solve this problem using Pikaia, we need to create a fitness function, which is given below:
subroutine obj_func(me,x,f)
!Pikaia fitness function for an Earth-Mars free return
use fortran_astrodynamics_toolkit
implicit none
class(pikaia_class),intent(inout) :: me !pikaia class
real(wp),dimension(:),intent(in) :: x !optimization variable vector
real(wp),intent(out) :: f !fitness value
real(wp),dimension(6) :: rv_earth_0, rv_mars, rv_earth_f
real(wp),dimension(3) :: v1,v2,v3,v4,vinf_0,vinf_f,vinfm,vinfp
real(wp) :: jd_earth_0,jd_mars,jd_earth_f,&
dt_earth_out,dt_earth_return,&
rp_penalty,vinf_penalty,e,delta,rp,vinfmag
real(wp),parameter :: mu_sun = 132712440018.0_wp !sun grav param [km3/s2]
real(wp),parameter :: mu_mars = 42828.0_wp !mars grav param [km3/s2]
real(wp),parameter :: rp_mars_min = 3390.0_wp+160.0_wp !min flyby radius at mars [km]
real(wp),parameter :: vinf_weight = 1000.0_wp !weights for the
real(wp),parameter :: rp_weight = 10.0_wp ! penalty functions
!get times:
jd_earth_0 = mjd_to_jd(x(1)) !julian date of earth departure
dt_earth_out = x(2) !outbound flyby time [days]
dt_earth_return = x(3) !return flyby time [days]
jd_mars = jd_earth_0 + dt_earth_out !julian date of mars flyby
jd_earth_f = jd_mars + dt_earth_return !julian date of earth arrival
!get earth/mars locations (wrt Sun):
call get_state(jd_earth_0,3,11,rv_earth_0) !earth at departure
call get_state(jd_mars, 4,11,rv_mars) !mars at flyby
call get_state(jd_earth_f,3,11,rv_earth_f) !earth at arrival
!compute lambert maneuvers:
call lambert(rv_earth_0,rv_mars, dt_earth_out*day2sec, mu_sun,v1,v2) !outbound
call lambert(rv_mars, rv_earth_f,dt_earth_return*day2sec,mu_sun,v3,v4) !return
!compute v-inf vectors:
vinf_0 = v1 - rv_earth_0(4:6) !earth departure
vinfm = v2 - rv_mars(4:6) !mars flyby (incoming)
vinfp = v3 - rv_mars(4:6) !mars flyby (outgoing)
vinf_f = v4 - rv_earth_f(4:6) !earth return
!the turning angle is the angle between vinf- and vinf+
delta = angle_between_vectors(vinfm,vinfp) !turning angle [rad]
vinfmag = norm2(vinfm) !vinf vector mag (incoming) [km/s]
e = one/sin(delta/two) !eccentricity
rp = mu_mars/(vinfmag*vinfmag)*(e-one) !periapsis radius [km]
!the constraints are added to the fitness function as penalties:
if (rp>=rp_mars_min) then
rp_penalty = zero !not active
else
rp_penalty = rp_mars_min - rp
end if
vinf_penalty = abs(norm2(vinfm) - norm2(vinfp))
!fitness function (to maximize):
f = - ( norm2(vinf_0) + &
norm2(vinf_f) + &
vinf_weight*vinf_penalty + &
rp_weight*rp_penalty )
end subroutine obj_func
The lambert routine called here is simply a wrapper to solve_lambert_gooding that computes both the "short way" and "long way" transfers, and returns the one with the lowest total \(\Delta v\). The two constraints are added to the objective function as penalties (to be driven to zero). Pikaia is then initialized and called by:
program flyby
use pikaia_module
use fortran_astrodynamics_toolkit
implicit none
integer,parameter :: n = 3
type(pikaia_class) :: p
real(wp),dimension(n) :: x,xl,xu
integer :: status,iseed
real(wp) :: f
!set random number seed:
iseed = 371
!bounds:
xl = [jd_to_mjd(julian_date(2018,1,1,0,0,0)), 100.0_wp,100.0_wp]
xu = [jd_to_mjd(julian_date(2018,12,31,0,0,0)),400.0_wp,400.0_wp]
call p%init(n,xl,xu,obj_func,status,&
ngen = 1000, &
np = 200, &
nd = 9, &
ivrb = 0, &
convergence_tol = 1.0e-6_wp, &
convergence_window = 200, &
initial_guess_frac = 0.0_wp, &
iseed = iseed )
call p%solve(x,f,status)
end program flyby
The three optimization variables are bounded: the Earth departure epoch must occur sometime in 2018, and the outbound and return flight times must each be between 100 and 400 days.
Running this program, we can get different solutions (depending on the value set for the random seed, and also the Pikaia settings). The best one I've managed to get with minimal tweaking is this:
- Earth departure epoch: MJD 58120 (Jan 2, 2018)
- Outbound flight time: 229 days
- Return flight time: 271 days
Which is similar to the solution shown in [2].
References
- R.H. Gooding, "A procedure for the solution of Lambert's orbital boundary-value problem", Celestial Mechanics and Dynamical Astronomy, Vol. 48, No. 2, 1990.
- Dennis Tito's 2021 Human Mars Flyby Mission Explained. SPACE.com, February 27, 2014.
- J.E. Prussing, B.A. Conway, "Orbital Mechanics", Oxford University Press, 1993.
Mar 09, 2015
I've started a new project on Github for a new modern object-oriented version of the Pikaia genetic algorithm code. This is a refactoring and upgrade of the Pikaia code from the High Altitude Observatory. The original code is public domain and was written by Paul Charbonneau & Barry Knapp (version 1.2 was released in 2003). The new code differs from the old code in the following respects:
- The original fixed-form source (FORTRAN 77) was converted to free-form source.
- The code is now object-oriented Fortran 2003/2008. All user interaction is now through a class, which is the only public entity in the module.
- All real variables are now 8 bytes (a.k.a. "double precision"). The precision can also be changed by the user by modifying the
wp parameter.
- The random number generator was replaced with calls to the intrinsic Fortran
random_number function.
- There are various new options (e.g., a convergence window with a tolerance can be specified as a stopping condition, and the user can specify a subroutine for reporting the best solution at each generation).
- Mapping the variables to be between 0 and 1 now occurs internally, rather than requiring the user to do it.
- Can now include an initial guess in the initial population.
This is another example of how older Fortran codes can be refactored to bring them up to date with modern computing concepts without doing that much work. In my opinion, the object-oriented Fortran 2003 interface is a lot better than the old FORTRAN 77 version. For one, it's easier to follow. Also, data can now easily be passed into the user fitness function by extending the pikaia class and putting the data there. No common blocks necessary!
References
- Original Pikaia code and documentation [High Altitude Observatory]









