Mar 14, 2016
Fortran namelists are a quick and dirty way of reading and writing variables to and from a file. It is actually the only high-level file access feature built into the Fortran language, in the sense of being able to read and write a complex formatted file with one line of code. Nowadays, I would recommend against using this feature since the format is not really a standard and varies from compiler to compiler, and there aren't good parsers available for other languages (with the notable exception of Python). There are better configuration file formats available today such as JSON. However, namelists can still be encountered in legacy applications, and may still be useful to the lazy programmer.
One of the problems with namelists is that all the variables in the file have to correspond exactly in name, type, rank, and size to variables declared in your code. Syntax errors in the file are not easily detected and a failed read due to an unexpected variable will usually just return a non-zero status code that isn't really much help in diagnosing the problem.
However, there is a way to output the line where the failure occurred on a namelist read, which can be quite useful for debugging. Say your code is expecting a namelist containing three real variables a, b, and c. However, the file contains the unexpected variable d like so:
&my_namelist
a = 1.0,
b = 2.0,
d = 3.0,
c = 4.0
/
Now consider the following Fortran code to read it:
program namelist_test
use iso_fortran_env, wp => real64
implicit none
real(wp) :: a,b,c ! namelist variables
integer :: istat,iunit
character(len=1000) :: line
namelist /my_namelist/ a,b,c
open(newunit=iunit,file='my_namelist.nml',&
status='OLD')
read(iunit, nml=my_namelist, iostat=istat)
if (istat/=0) then
backspace(iunit)
read(iunit,fmt='(A)') line
write(error_unit,'(A)') &
'Invalid line in namelist: '//trim(line)
end if
close(iunit)
end program namelist_test
The READ statement will fail with a non-zero istat code. Then we simply use the BACKSPACE function, which moves the file position back one record (the record where the read failed). Then we can simply read this line and print it. This code produces the following error message:
Invalid line in namelist: d = 3.0,
Feb 28, 2016
Some years ago, I needed a Fortran routine to do linear interpolation of a multidimensional (up to 6D) data set. Not wanting to reinvent the wheel, I ended up using a routine called FINT from CERNLIB (documentation here). It is written in Fortran 66, and has some hard-coded limits on the number of dimensions that can be used, but these are not fundamental to the algorithm. With a few minor changes, the routine can be used for interpolation of any number of dimensions. I present below a modern Fortran version that removes the limitations. Note that the original code is GPL licensed, thus so is this modification.
function fint(narg,arg,nent,ent,table)
use iso_fortran_env, only: wp => real64
implicit none
real(wp) :: fint
integer,intent(in) :: narg
integer,dimension(narg),intent(in) :: nent
real(wp),dimension(narg),intent(in) :: arg
real(wp),dimension(:),intent(in) :: ent
real(wp),dimension(:),intent(in) :: table
integer,dimension(2**narg) :: index
real(wp),dimension(2**narg) :: weight
logical :: mflag,rflag
real(wp) :: eta,h,x
integer :: i,ishift,istep,k,knots,lgfile,&
lmax,lmin,loca,locb,locc,ndim
!some error checks:
if (size(ent)/=sum(nent)) &
error stop 'size of ent is incorrect.'
if (size(table)/=product(nent)) &
error stop 'size of table is incorrect.'
if (narg<1) &
error stop 'invalid value of narg.'
lmax = 0
istep = 1
knots = 1
index(1) = 1
weight(1) = 1.0_wp
main: do i = 1 , narg
x = arg(i)
ndim = nent(i)
loca = lmax
lmin = lmax + 1
lmax = lmax + ndim
if ( ndim>2 ) then
locb = lmax + 1
do
locc = (loca+locb)/2
if ( x<ent(locc) ) then
locb = locc
else if ( x==ent(locc) ) then
ishift = (locc-lmin)*istep
do k = 1 , knots
index(k) = index(k) + ishift
end do
istep = istep*ndim
cycle main
else
loca = locc
end if
if ( locb-loca<=1 ) exit
end do
loca = min(max(loca,lmin),lmax-1)
ishift = (loca-lmin)*istep
eta = (x-ent(loca))/(ent(loca+1)-ent(loca))
else
if ( ndim==1 ) cycle main
h = x - ent(lmin)
if ( h==0.0_wp ) then
istep = istep*ndim
cycle main
end if
ishift = istep
if ( x-ent(lmin+1)==0.0_wp ) then
do k = 1 , knots
index(k) = index(k) + ishift
end do
istep = istep*ndim
cycle main
end if
ishift = 0
eta = h/(ent(lmin+1)-ent(lmin))
end if
do k = 1 , knots
index(k) = index(k) + ishift
index(k+knots) = index(k) + istep
weight(k+knots) = weight(k)*eta
weight(k) = weight(k) - weight(k+knots)
end do
knots = 2*knots
istep = istep*ndim
end do main
fint = 0.0_wp
do k = 1 , knots
i = index(k)
fint = fint + weight(k)*table(i)
end do
end function fint
As I recall, I wrote wrappers to this function in order to be able to input the data in a more reasonable format. For example, for a five dimensional data set it is more natural to input the five rank-1 abscissa vectors and the rank-5 ordinate matrix. The disadvantage of this routine is that you have to stuff the ordinate matrix into a vector (as well as stuffing all the abscissa vectors into a single vector). This could also be an advantage in some cases, since Fortran arrays have a maximum rank. For Fortran 90, it was 7, while Fortran 2008 expanded this to 15 (the current Intel Fortran Compiler allows up to 31 as a non-standard extension). If you ever, for example, needed to interpolate 32-dimensional data (assuming you had enough RAM), you could do it with FINT without having to declare any rank-32 matrices. In any event, an example 5D wrapper for FINT is given here:
function fint_5d_wrapper(x,y,z,q,r,&
xvec,yvec,zvec,qvec,&
rvec,fmat) result(f)
use iso_fortran_env, only: wp => real64
implicit none
integer,parameter :: narg = 5
real(wp) :: f
real(wp),intent(in) :: x,y,z,q,r
real(wp),dimension(:),intent(in) :: xvec
real(wp),dimension(:),intent(in) :: yvec
real(wp),dimension(:),intent(in) :: zvec
real(wp),dimension(:),intent(in) :: qvec
real(wp),dimension(:),intent(in) :: rvec
real(wp),dimension(:,:,:,:,:),intent(in) :: fmat
integer,dimension(narg) :: nent
nent(1) = size(xvec)
nent(2) = size(yvec)
nent(3) = size(zvec)
nent(4) = size(qvec)
nent(5) = size(rvec)
f = fint(narg,[x,y,z,q,r],nent,&
[xvec,yvec,zvec,qvec,rvec],&
reshape(fmat,[product(nent)]))
end function fint_5d_wrapper
This works well enough, but note that it isn't very computationally efficient since we are creating temporary copies of the potentially large data arrays (including having to reshape a rank-5 matrix) every time we do an interpolation. While the logic of FINT is a bit hard to fathom, the actual equations are fairly simple (see here, for example). What we really need now is an object-oriented modern Fortran library for multidimensional linear interpolation. Stay tuned...
References
Feb 22, 2016
Intel has released version 16.0.2 of the Intel Fortran Compiler (which is part of Intel Parallel Studio XE 2016). It looks like mainly a bug-fix release. Microsoft Visual Studio 2015 Update 1 is now also officially supported.
References
Jan 31, 2016

Thaddeus Vincenty (1920--2002) Image source: IAG Newsletter
There are two standard problems in geodesy:
- Direct geodetic problem -- Given a point on the Earth (latitude and longitude) and the direction (azimuth) and distance from that point to a second point, determine the latitude and longitude of that second point.
- Inverse geodetic problem -- Given two points on the Earth, determine the azimuth and distance between them.
Assuming the Earth is an oblate spheroid, both of these can be solved using the iterative algorithms by Thaddeus Vincenty [1]. Modern Fortran versions of Vincenty's algorithms can be found in the geodesy module of the Fortran Astrodynamics Toolkit [2].
The direct algorithm was listed in an earlier post. If we assume a WGS84 Earth ellipsoid (a=6378.137 km, f=1/298.257223563), an example direct calculation is:
$$
\begin{array}{rcll}
\phi_1 &= & 29.97^{\circ} & \mathrm{(Latitude ~of ~ first ~ point)}\\
\lambda_1 &= & -95.35^{\circ} & \mathrm{(Longitude ~of ~ first ~point)} \\
Az &= & 20^{\circ} & \mathrm{(Azimuth)}\\
s &= & 50~\mathrm{km} & \mathrm{(Distance)}
\end{array}
$$
The latitude and longitude of the second point is:
$$
\begin{array}{rcl}
\phi_2 &= & 30.393716^{\circ} \\
\lambda_2 &= & -95.172057^{\circ} \\
\end{array}
$$
The more complicated inverse algorithm is listed here (based on the USNGS code from [1]):
subroutine inverse(a, rf, b1, l1, b2, l2, faz, baz, s, it, sig, lam, kind)
use, intrinsic :: iso_fortran_env, wp => real64
implicit none
real(wp), intent(in) :: a !! Equatorial semimajor axis
real(wp), intent(in) :: rf !! reciprocal flattening (1/f)
real(wp), intent(in) :: b1 !! latitude of point 1 (rad, positive north)
real(wp), intent(in) :: l1 !! longitude of point 1 (rad, positive east)
real(wp), intent(in) :: b2 !! latitude of point 2 (rad, positive north)
real(wp), intent(in) :: l2 !! longitude of point 2 (rad, positive east)
real(wp), intent(out) :: faz !! Forward azimuth (rad, clockwise from north)
real(wp), intent(out) :: baz !! Back azimuth (rad, clockwise from north)
real(wp), intent(out) :: s !! Ellipsoidal distance
integer, intent(out) :: it !! iteration count
real(wp), intent(out) :: sig !! spherical distance on auxiliary sphere
real(wp), intent(out) :: lam !! longitude difference on auxiliary sphere
integer, intent(out) :: kind !! solution flag: kind=1, long-line; kind=2, antipodal
real(wp) :: beta1, beta2, biga, bigb, bige, bigf, boa, &
c, cosal2, coslam, cossig, costm, costm2, &
cosu1, cosu2, d, dsig, ep2, l, prev, sinal, &
sinlam, sinsig, sinu1, sinu2, tem1, tem2, &
temp, test, z
real(wp), parameter :: pi = acos(-1.0_wp)
real(wp), parameter :: two_pi = 2.0_wp*pi
real(wp), parameter :: tol = 1.0e-14_wp !! convergence tolerance
real(wp), parameter :: eps = 1.0e-15_wp !! tolerance for zero
boa = 1.0_wp - 1.0_wp/rf
beta1 = atan(boa*tan(b1))
sinu1 = sin(beta1)
cosu1 = cos(beta1)
beta2 = atan(boa*tan(b2))
sinu2 = sin(beta2)
cosu2 = cos(beta2)
l = l2 - l1
if (l > pi) l = l - two_pi
if (l < -pi) l = l + two_pi
prev = l
test = l
it = 0
kind = 1
lam = l
longline: do ! long-line loop (kind=1)
sinlam = sin(lam)
coslam = cos(lam)
temp = cosu1*sinu2 - sinu1*cosu2*coslam
sinsig = sqrt((cosu2*sinlam)**2 + temp**2)
cossig = sinu1*sinu2 + cosu1*cosu2*coslam
sig = atan2(sinsig, cossig)
if (abs(sinsig) < eps) then
sinal = cosu1*cosu2*sinlam/sign(eps, sinsig)
else
sinal = cosu1*cosu2*sinlam/sinsig
end if
cosal2 = -sinal**2 + 1.0_wp
if (abs(cosal2) < eps) then
costm = -2.0_wp*(sinu1*sinu2/sign(eps, &
cosal2)) + cossig
else
costm = -2.0_wp*(sinu1*sinu2/cosal2) + &
cossig
end if
costm2 = costm*costm
c = ((-3.0_wp*cosal2 + 4.0_wp)/rf + 4.0_wp)* &
cosal2/rf/16.0_wp
antipodal: do ! antipodal loop (kind=2)
it = it + 1
d = (((2.0_wp*costm2 - 1.0_wp)*cossig*c + &
costm)*sinsig*c + sig)*(1.0_wp - c)/rf
if (kind == 1) then
lam = l + d*sinal
if (abs(lam - test) >= tol) then
if (abs(lam) > pi) then
kind = 2
lam = pi
if (l < 0.0_wp) lam = -lam
sinal = 0.0_wp
cosal2 = 1.0_wp
test = 2.0_wp
prev = test
sig = pi - abs(atan(sinu1/cosu1) + &
atan(sinu2/cosu2))
sinsig = sin(sig)
cossig = cos(sig)
c = ((-3.0_wp*cosal2 + 4.0_wp)/rf + &
4.0_wp)*cosal2/rf/16.0_wp
if (abs(sinal - prev) < tol) exit longline
if (abs(cosal2) < eps) then
costm = -2.0_wp*(sinu1*sinu2/ &
sign(eps, cosal2)) + cossig
else
costm = -2.0_wp*(sinu1*sinu2/cosal2) + &
cossig
end if
costm2 = costm*costm
cycle antipodal
end if
if (((lam - test)*(test - prev)) < 0.0_wp .and. it > 5) &
lam = (2.0_wp*lam + 3.0_wp*test + prev)/6.0_wp
prev = test
test = lam
cycle longline
end if
else
sinal = (lam - l)/d
if (((sinal - test)*(test - prev)) < 0.0_wp .and. it > 5) &
sinal = (2.0_wp*sinal + 3.0_wp*test + prev)/6.0_wp
prev = test
test = sinal
cosal2 = -sinal**2 + 1.0_wp
sinlam = sinal*sinsig/(cosu1*cosu2)
coslam = -sqrt(abs(-sinlam**2 + 1.0_wp))
lam = atan2(sinlam, coslam)
temp = cosu1*sinu2 - sinu1*cosu2*coslam
sinsig = sqrt((cosu2*sinlam)**2 + temp**2)
cossig = sinu1*sinu2 + cosu1*cosu2*coslam
sig = atan2(sinsig, cossig)
c = ((-3.0_wp*cosal2 + 4.0_wp)/rf + 4.0_wp)* &
cosal2/rf/16.0_wp
if (abs(sinal - prev) >= tol) then
if (abs(cosal2) < eps) then
costm = -2.0_wp*(sinu1*sinu2/ &
sign(eps, cosal2)) + cossig
else
costm = -2.0_wp*(sinu1*sinu2/cosal2) + &
cossig
end if
costm2 = costm*costm
cycle antipodal
end if
end if
exit longline
end do antipodal
end do longline
if (kind == 2) then ! antipodal
faz = sinal/cosu1
baz = sqrt(-faz**2 + 1.0_wp)
if (temp < 0.0_wp) baz = -baz
faz = atan2(faz, baz)
tem1 = -sinal
tem2 = sinu1*sinsig - cosu1*cossig*baz
baz = atan2(tem1, tem2)
else ! long-line
tem1 = cosu2*sinlam
tem2 = cosu1*sinu2 - sinu1*cosu2*coslam
faz = atan2(tem1, tem2)
tem1 = -cosu1*sinlam
tem2 = sinu1*cosu2 - cosu1*sinu2*coslam
baz = atan2(tem1, tem2)
end if
if (faz < 0.0_wp) faz = faz + two_pi
if (baz < 0.0_wp) baz = baz + two_pi
ep2 = 1.0_wp/(boa*boa) - 1.0_wp
bige = sqrt(1.0_wp + ep2*cosal2)
bigf = (bige - 1.0_wp)/(bige + 1.0_wp)
biga = (1.0_wp + bigf*bigf/4.0_wp)/(1.0_wp - bigf)
bigb = bigf*(1.0_wp - 0.375_wp*bigf*bigf)
z = bigb/6.0_wp*costm*(-3.0_wp + 4.0_wp* &
sinsig**2)*(-3.0_wp + 4.0_wp*costm2)
dsig = bigb*sinsig*(costm + bigb/4.0_wp* &
(cossig*(-1.0_wp + 2.0_wp*costm2) - z))
s = (boa*a)*biga*(sig - dsig)
end subroutine inverse
For the same ellipsoid, an example inverse calculation is:
$$
\begin{array}{rcll}
\phi_1 &= & 29.97^{\circ} & \mathrm{(Latitude ~of ~ first ~ point)}\\
\lambda_1 &= & -95.35^{\circ} & \mathrm{(Longitude ~of ~ first ~point)} \\
\phi_2 &= & 40.77^{\circ} & \mathrm{(Latitude ~of ~ second ~ point)}\\
\lambda_2 &= & -73.98^{\circ} & \mathrm{(Longitude ~of ~ second ~point)}
\end{array}
$$
The azimuth and distance from the first to the second point is:
$$
\begin{array}{rcl}
Az &= & 52.400056^{\circ} & \mathrm{(Azimuth)}\\
s &= & 2272.497~\mathrm{km} & \mathrm{(Distance)}
\end{array}
$$
References
Jan 12, 2016
SLSQP [1-2] is a sequential quadratic programming (SQP) optimization algorithm written by Dieter Kraft in the 1980s. It can be used to solve nonlinear programming problems that minimize a scalar function:
$$
f(\mathbf{x})
$$
subject to general equality and inequality constraints:
$$
\begin{array}{rl} g_j(\mathbf{x}) = \mathbf{0} & j = 1, \dots ,m_e \\
g_j(\mathbf{x}) \ge \mathbf{0} & j = m_e+1, \dots ,m \end{array}
$$
and to lower and upper bounds on the variables:
$$
\begin{array}{rl} l_i \le x_i \le u_i & i = 1, \dots ,n \end{array}
$$
SLSQP was written in Fortran 77, and is included in PyOpt (called using Python wrappers) and NLopt (as an f2c translation of the original source). It is also included as one of the solvers in two of NASA's trajectory optimization tools (OTIS and Copernicus).
The code is pretty old school and includes numerous obsolescent Fortran features such as arithmetic IF statements, computed and assigned GOTO statements, statement functions, etc. It also includes some non-standard assumptions (implicit saving of variables and initialization to zero).
So, the time is ripe for refactoring SLSQP. Which is what I've done. The refactored version includes some new features and bug fixes, including:
- It is now thread safe. The original version was not thread safe due to the use of saved variables in one of the subroutines.
- It should now be 100% standard compliant (Fortran 2008).
- It now has an easy-to-use object-oriented interface. The
slsqp_class is used for all interactions with the solver. Methods include initialize(), optimize(), and destroy().
- It includes updated versions of some of the third-party routines used in the original code (BLAS, LINPACK, and NNLS).
- It has been translated into free-form source. For this, I used the sample online version of the SPAG Fortran Code Restructuring tool to perform some of the translation, which seemed to work really well. The rest I did manually. Fixed-form source (FORTRAN 77 style) is terrible and needs to die. There's no reason to be using it 25 years after the introduction of free-form source (yes, I'm talking to you Claus 😀).
- The documentation strings in the code have been converted to FORD format, allowing for nicely formatted documentation to be auto-generated (which includes MathJax formatted equations to replace the ASCII ones in the original code). It also generates ultra-slick call graphs like the one below.
- A couple of bug fixes noted elsewhere have been applied (see here and here).
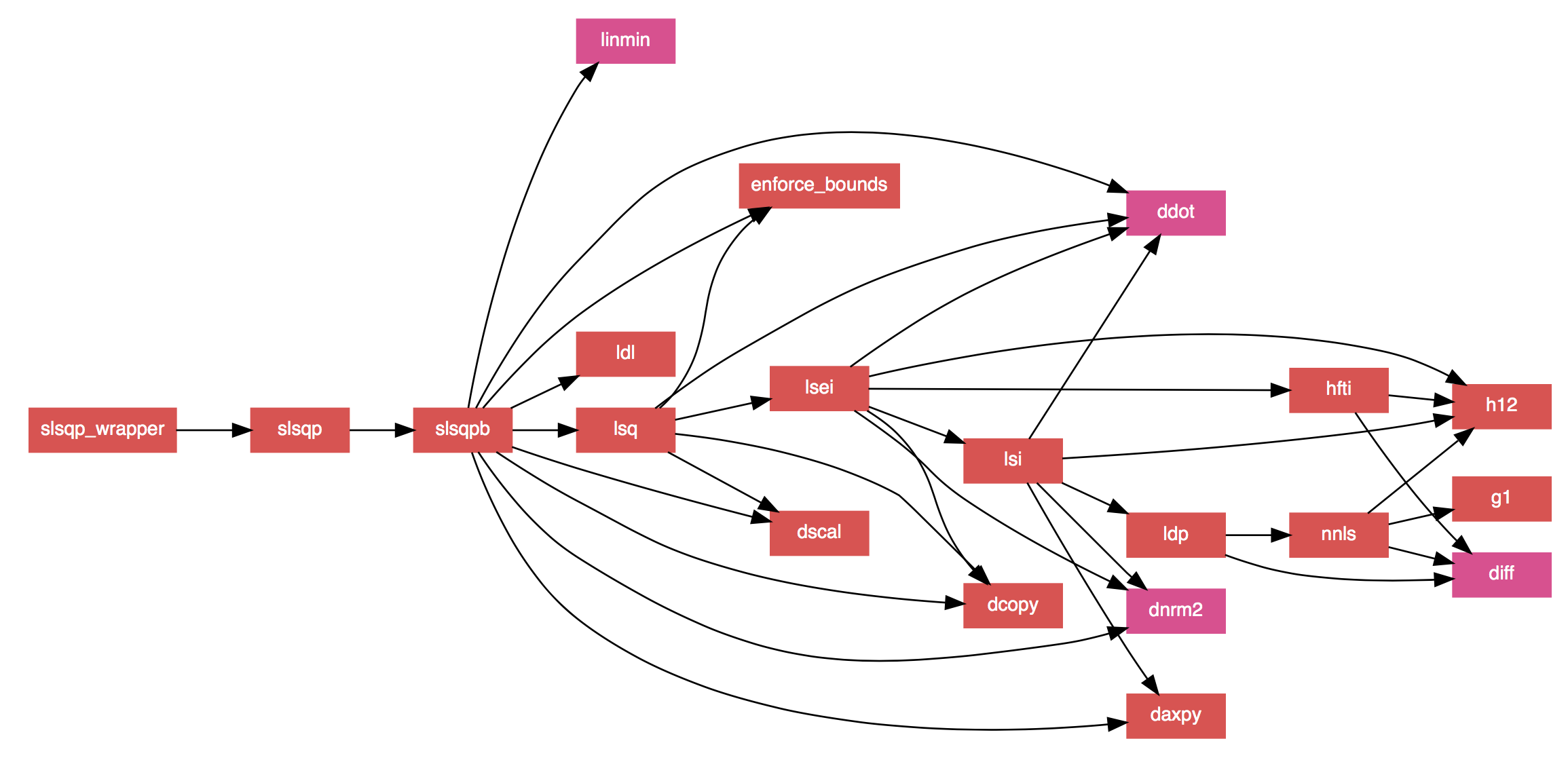
SLSQP call graph generated by FORD.
The original code used a "reverse communication" interface, which was one of the workarounds used in old Fortran code to make up for the fact that there wasn't really a good way to pass arbitrary data into a library routine. So, the routine returns after called, requests data, and then is called again. For now, I've kept the reverse communication interface in the core routines (the user never interacts with them directly, however). Eventually, I may do away with this, since I don't think it's particularly useful anymore.
The new code is on GitHub, and is released under a BSD license. There are various additional improvements that could be made, so I'll continue to tinker with it, but for now it seems to work fine. If anyone else finds the new version useful, I'd be interested to hear about it.
See Also
- Dieter Kraft, "A Software Package for Sequential Quadratic Programming", DFVLR-FB 88-28, 1988.
- Dieter Kraft, "Algorithm 733: TOMP–Fortran Modules for Optimal Control Calculations," ACM Transactions on Mathematical Software, Vol. 20, No. 3, p. 262-281 (1994).
Dec 28, 2015

DDEABM is variable step size, variable order Adams-Bashforth-Moulton PECE solver for integrating a system of first order ordinary differential equations [1-2]. It is a public-domain code originally developed in the 1970s-1980s, written in FORTRAN 77, and is available from Netlib (as part of the SLATEC Common Mathematical Library). DDEABM is primarily designed to solve non-stiff and mildly-stiff differential equations when derivative evaluations are expensive, high accuracy results are needed or answers at many specific points are required. It is based on the earlier ODE/STEP/INTRP codes described in [3-4].
DDEABM is a great code, but like many of the greats of Fortran, it seems to have been frozen in amber for 30 years. There are a couple of translations into other programming languages out there such as IDL and Matlab. It is also the ancestor of the Matlab ode113 solver (indeed, they were both written by the same person [5]). But, it looks like poor Fortran users have been satisfied with using it as is, in all its FORTRAN 77 glory.
So, I've taken the code and significantly refactored it to bring it up to date to modern standards (Fortran 2003/2008). This is more than just a conversion from fixed to free-form source. The updated version is now object-oriented and thread-safe, and also has a new event finding capability (there is a version of this code that had root-finding capability, but it seems to be based on an earlier version of the code, and also has some limitations such as a specified maximum number of equations). The new event finding feature incorporates the well-known ZEROIN algorithm [6-7] for finding a root on a bracketed interval. Everything is wrapped up in an easy-to-use class, and it also supports the exporting of intermediate integration points.
The new code is available on GitHub and is released under a permissive BSD-style license. It is hoped that it will be useful. There are some other great ODE codes that could use the same treatment (e.g. DLSODE/DVODE from ODEPACK, DIVA from MATH77, and DOP853 from Ernst Hairer).
References
- L. F. Shampine, H. A. Watts, "DEPAC - Design of a user oriented package of ode solvers", Report SAND79-2374, Sandia Laboratories, 1979.
- H. A. Watts, "A smoother interpolant for DE/STEP, INTRP and DEABM: II", Report SAND84-0293, Sandia Laboratories, 1984.
- L. F. Shampine, M. K. Gordon, "Solving ordinary differential equations with ODE, STEP, and INTRP", Report SLA-73-1060, Sandia Laboratories, 1973.
- L. F. Shampine, M. K. Gordon, "Computer solution of ordinary differential equations, the initial value problem", W. H. Freeman and Company, 1975.
- L. F. Shampine and M. W. Reichelt, "The MATLAB ODE Suite" [MathWorks].
- R. P. Brent, "An algorithm with guaranteed convergence for finding a zero of a function", The Computer Journal, Vol 14, No. 4., 1971.
- R. P. Brent, "Algorithms for minimization without derivatives", Prentice-Hall, Inc., 1973.
Nov 13, 2015

Good news everyone! The US government just announced that it has reached an agreement with NVIDIA to produce an open source Fortran front-end for the LLVM compiler infrastructure. It will be based on the existing commercial Portland Group compiler (NVIDIA purchased the Portland Group a couple of years ago). Source code for the Fortran front-end is expected to be available in late 2016. From the announcement:
The project is being spearheaded by the Lawrence Livermore, Sandia and Los Alamos national laboratories in response to the need for a robust open-source Fortran solution to complement and support the burgeoning use of LLVM and the CLANG C++ compiler in the HPC community. Large HPC applications, such as those developed by the NNSA Laboratories, are often built on mixed-language modules, and require a common compiler infrastructure that supports both C/C++ and Fortran. Fortran also remains widely used in the broader scientific computing community, supporting simulation science to advance national security, medicine, energy, climate and basic science missions.
Does Fortran support for LLVM mean that we'll eventually be able to have Fortran code running on our iPads? Only time will tell...
See also
Nov 06, 2015
My bspline-fortran multidimensional interpolation library is now at version 4.0. The documentation can be found here. Since I first mentioned it here, I've made many updates to this library, including:
- Added object-oriented wrappers to the core routines. The user now has the choice to use the older subroutine interface or the new object-oriented interface.
- Added a set of 1D routines (suggested by a user on GitHub). The library now works for 1D-6D data sets.
- Everything is now thread-safe for your multithreaded pleasure.
The new object-oriented interface makes it pretty easy to use from modern Fortran. The classes have only three methods (initialize, evaluate, and destroy). For example, a 3D case would look like this:
type(bspline_3d) :: s
call s%initialize(x,y,z,fcn,kx,ky,kz,iflag)
call s%evaluate(xval,yval,zval,idx,idy,idz,f,iflag)
call s%destroy()
The core routines of bspline-fortran were written in the early 1980s. Good Fortran code can live on for decades after it is written. While this is great, it also means that there is a lot of old Fortran code out there that is written in a coding style that no modern programmer should accept. This can be OK for well documented library routines that the user never needs to change (see, for example SPICE or LAPACK). However, refactoring old code using modern concepts can provide many advantages, as is demonstrated in this case.
See also
- DBSPLIN and DTENSBS from the NIST Core Math Library.
- Carl de Boor, A Practical Guide to Splines, Springer-Verlag, New York, 1978.
Oct 17, 2015
Fortran's TRANSFER function (introduced in Fortran 95) is a somewhat strange function that can be used to do some interesting things not otherwise possible in earlier versions of the language. In fact, it can be used to achieve a sort of poor-man's polymorphism. It can also still be useful in modern Fortran.
All this function does is transfers the bitwise representation of one variable into another variable. This is different from casting a variable of one type to another. For example:
program transfer_example
use iso_fortran_env
integer(int64) :: i
real(real64) :: d
i = 1
d = i !d is 1.0000000000000000
d = transfer(i,d) !d is 4.9406564584124654E-324
end program transfer_example
The following example shows how to use TRANSFER to create a hash function that can operate on any variable or derived type. The dummy argument of the hash_anything function is an unlimited polymorphic variable (class(*)). The bitwise representation of this variable is then transferred into a character string big enough to hold it (making use of the Fortran 2008 STORAGE_SIZE intrinsic), which can then be hashed using any hash function that takes a character string as an input (a basic DJB method is used here).
module hash_module
!integer kind to use for the hash:
use iso_fortran_env, only: ip => INT32
implicit none
contains
function hash_anything(v) result(hash)
!! Hash anything, using unlimited
!! polymorphic variable and transfer()
class(*),intent(in) :: v
integer(ip) :: hash
!!a default character string
!!with the same size as v:
character(len=ceiling(dble(storage_size(v))/&
dble(storage_size(' ')))) :: str
str = transfer(v,str) !transfer bits of v into
!string of the same size
hash = djb_hash(str) !hash it
end function hash_anything
function djb_hash(str) result(hash)
!! Character string hashing with
!! the DJB algorithm. From [1].
character(len=*),intent(in) :: str
integer(ip) :: hash
integer :: i
hash = 5381_ip
do i=1,len(str)
hash = (ishft(hash,5_ip) + hash) + &
ichar(str(i:i))
end do
end function djb_hash
end module hash_module
See also
- Fortran hashing algorithm, July 6, 2013 [Fortran Dev]
- Hash table example [Fortran Wiki]
Aug 27, 2015
Hey, there's an article on the internet that mentions Coarray Fortran (introduced in the Fortran 2008 standard), and how it is the right tool for a particular massive computational job. It doesn't mention punchcards, the 1950s, or express any surprise that people are still using Fortran in modern times. Progress?
Excerpt:
Applications such as ECMWF's IFS model use OpenMP (a standard for shared memory parallelization) for computations on the nodes and MPI for communications across the nodes. Generally, this arrangement works well for many applications, but for high-resolution weather modeling using the spectral transform method, it can bog down the application, wasting precious runtime—it simply does not easily allow for any overlap of computation and communication. The use of coarrays (also called PGAS, for Partitioned Global Address Space) in Fortran, however, allows a simple syntax for data to be communicated between tasks at the same time computations are being performed.
See also






