The 4.2.0 release of the JSON-Fortran library is now available on GitHub. This version has a few new features and a couple of minor bug fixes. The source code documentation is also now produced by FORD, which is a great new tool for modern Fortran documentation. It has been out for less than a year and is already far better than other tools that have been around for years. See an example of the output here.
It looks like JPL just opensourced their MATH77 Fortran library. MATH77 is a library of Fortran 77 subroutines implementing various numerical algorithms. It was developed over decades at JPL, and contains some very high-quality and time-tested code. The code is released under a BSD-type license. There is also a C version for people who love semicolons.
Good news for starving students: Intel just announced that their compilers (including the Intel Fortran compiler) are now available under a free, non-commercial license for qualified students on Linux, MacOS X and Windows.
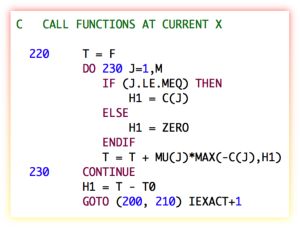
SLSQP [1-2] is a sequential least squares constrained optimization algorithm written by Dieter Kraft in the 1980s. Today, it forms part of the Python pyOpt package for solving nonlinear constrained optimization problems. It was written in FORTRAN 77, and is filled with such ancient horrors like arithmetic IF statements, GOTO statements (even computed and assigned GOTO statements), statement functions, etc. It also assumes the implicit saving of variables in the LINMIN subroutine (which is totally non-standard, but was done by some early compilers), and in some instances assumes that variables are initialized with a zero value (also non-standard, but also done by some compilers). It has an old-fashioned "reverse communication" style interface, with generous use of "WORK" arrays passed around using assumed-size dummy arguments. The pyOpt users don't seem to mind all this, since they are calling it from a Python wrapper, and I guess it works fine (for now).
I don't know if anyone has ever tried to refactor this into modern Fortran with a good object-oriented interface. It seems like it would be a good idea. I've been toying with it for a while. It is always an interesting process to refactor old Fortran code. The fixed-form to free-form conversion can usually be done fairly easily with an automated script, but untangling the spaghetti can be a bit harder. Consider the following code snipet from the subroutine HFTI:
C DETERMINE PSEUDORANK
DO 90 j=1,ldiag
90 IF(ABS(a(j,j)).LE.tau) GOTO 100
k=ldiag
GOTO 110
100 k=j-1
110 kp1=k+1
A modern version that performs the exact same calculation is:
!determine pseudorank:
do j=1,ldiag
if (abs(a(j,j))<=tau) exit
end do
k=j-1
kp1=j
As you can see, no line numbers or GOTO statements are required. The new version even eliminates one assignment and one addition operation. Note that the refactored version depends on the fact that the index of the DO loop, if it completes the loop (i.e., if the exit statement is not triggered), will have a value of ldiag+1. This behavior has been part of the Fortran standard for some time (perhaps it was not when this routine was written?).
There is also a C translation of SLSQP available, which fixes some of the issues in the original code. Their version of the above code snippet is a pretty straightforward translation of the FORTRAN 77 version, except with all the ugliness of C on full display (a[j + j * a_dim1], seriously?):
/* DETERMINE PSEUDORANK */
i__2 = ldiag;
for (j = 1; j <= i__2; ++j) {
/* L90: */
if ((d__1 = a[j + j * a_dim1], fabs(d__1)) <= *tau) {
goto L100;
}
}
k = ldiag;
goto L110;
L100:
k = j - 1;
L110:
kp1 = k + 1;
Topological sorting can be used to determine the order in which a collection of interdependent tasks must be performed. For example, when building a complex modern Fortran application, there can be many modules with complex interdependencies (via use association). A Fortran building system (like FoBiS, Foray, or SCons) will perform a topological sort to determine the correct compilation order. In graph theory, the collection of tasks are vertices of a directed graph. If there are no circular dependencies, then it is a directed acyclic graph (DAG).
An example modern Fortran implementation of a topological sorting algorithm is given here. The only public class is dag, which is used to define the graph and perform the sort. The toposort method performs a "depth-first" traversal of the graph using the recursive subroutine dfs. Each vertex is only visited once, and so the algorithm runs in linear time. The routine also triggers an error message for circular dependencies.
module toposort_module
!! Topological sorting, using a recursive
!! depth-first method. The vertices are
!! integer values from (1, 2, ..., nvertices)
implicit none
private
type :: vertex
!! a vertex of a directed acyclic graph (DAG)
integer,dimension(:),allocatable :: edges
integer :: ivertex = 0 !vertex number
logical :: checking = .false.
logical :: marked = .false.
contains
procedure :: set_edges
end type vertex
type,public :: dag
!! a directed acyclic graph (DAG)
type(vertex),dimension(:),allocatable :: vertices
contains
procedure :: set_vertices => dag_set_vertices
procedure :: set_edges => dag_set_edges
procedure :: toposort => dag_toposort
end type dag
contains
subroutine set_edges(me,edges)
!! specify the edge indices for this vertex
implicit none
class(vertex),intent(inout) :: me
integer,dimension(:),intent(in) :: edges
allocate(me%edges(size(edges)))
me%edges = edges
end subroutine set_edges
subroutine dag_set_vertices(me,nvertices)
!! set the number of vertices in the dag
implicit none
class(dag),intent(inout) :: me
integer,intent(in) :: nvertices !! number of vertices
integer :: i
allocate(me%vertices(nvertices))
me%vertices%ivertex = [(i,i=1,nvertices)]
end subroutine dag_set_vertices
subroutine dag_set_edges(me,ivertex,edges)
!! set the edges for a vertex in a dag
implicit none
class(dag),intent(inout) :: me
integer,intent(in) :: ivertex !! vertex number
integer,dimension(:),intent(in) :: edges
call me%vertices(ivertex)%set_edges(edges)
end subroutine dag_set_edges
subroutine dag_toposort(me,order)
!! main toposort routine
implicit none
class(dag),intent(inout) :: me
integer,dimension(:),allocatable,intent(out) :: order
integer :: i,n,iorder
n = size(me%vertices)
allocate(order(n))
iorder = 0 ! index in order array
do i=1,n
if (.not. me%vertices(i)%marked) &
call dfs(me%vertices(i))
end do
contains
recursive subroutine dfs(v)
!! depth-first graph traversal
type(vertex),intent(inout) :: v
integer :: j
if (v%checking) then
error stop 'Error: circular dependency.'
else
if (.not. v%marked) then
v%checking = .true.
if (allocated(v%edges)) then
do j=1,size(v%edges)
call dfs(me%vertices(v%edges(j)))
end do
end if
v%checking = .false.
v%marked = .true.
iorder = iorder + 1
order(iorder) = v%ivertex
end if
end if
end subroutine dfs
end subroutine dag_toposort
end module toposort_module
An example use of this module is given below. Here, we define a graph with five vertices: task 2 depends on 1, task 3 depends on both 1 and 5, and task 4 depends on 5.
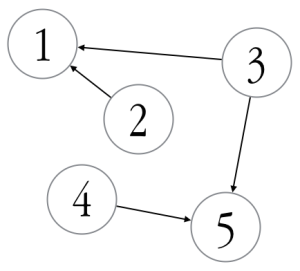
program main
use toposort_module
implicit none
type(dag) :: d
integer,dimension(:),allocatable :: order
call d%set_vertices(5)
call d%set_edges(2,[1]) ! 2 depends on 1
call d%set_edges(3,[5,1]) ! 3 depends on 5 and 1
call d%set_edges(4,[5]) ! 4 depends on 5
call d%toposort(order)
write(*,*) order
end program main
The result is:
Which is the evaluation order. As far as I can find, the above code is the only modern Fortran topological sorting implementation available on the internet. There is a FORTRAN 77 subroutine here, and a Fortran 90-ish one here (however, neither of them check for circular dependencies).
Part of the confusion about modern Fortran is what file extension to use. This confusion has its roots in the Fortran 90 standard (ISO/IEC 1539:1991) and the introduction of "free-form" source (the older FORTRAN 77 punched-card style was renamed "fixed-form" at this time). Unfortunately, compiler vendors began to use the extension .f90 for free-form files (common fixed-form extensions were .f or .for). Of course, the Fortran standard says nothing about file extensions. This is just one of those things the Lords of Fortran pretend are not important, like the ability to access the command line (not standardized until Fortran 2008) or the file system (still waiting for this). So, that left the compiler vendors (and users) free to do what they wanted, and all of them used .f90 for the new file type.
This was fine until the Fortran 95 standard came along (ISO/IEC 1539-1:1997). Fortran 95 was a minor update to the language (mostly cleaning up some of the half-baked bits of Fortran 90, but also adding some new stuff). This is when things started to go wrong. Since Fortran 90 used the .f90 extension, Fortran 95 should use .f95, right? And then Fortran 2003 came along, and then Fortran 2008, etc. The end result is a confusion of file extensions for free-form source such as .f90, .f95, .f03, .f08, and soon .f15. However, it doesn't make any sense to use the file extension to indicate the Fortran standard. Fortran has a high degree of backward compatibility (Python users take note). So, for example, almost all of Fortran 95 code is valid Fortran 90 code. Even a good deal of FORTRAN 77 code is still perfectly valid Fortran 2008 code. In fact, fixed-form source is still valid even in the Fortran 2008 standard (although only a lunatic would write object-oriented code in fixed-form format).
To sum up: .f90 means free-form source, not Fortran 90, and it's the only extension you should to be using. Stop the madness, or we're really going to be in trouble 75 years from now.
The GNU Project just announced the availability of GCC 5.1. There are various new GFortran features, including:
ieee_features, ieee_exceptions and ieee_arithmetic) from Fortran 2003.implicit none (external, type) from Fortran 2015.GFortran is still not completely Fortran 2003 compatible, however.
In Intel news, Intel Parallel Studio XE 2016 is now in beta (which includes v16 of the Intel Fortran Compiler). The major new features are:
impure elemental from Fortran 2008.Python's matplotlib.pyplot is a very nice collection of functions that provide an easy Matlab-like interface for data plotting. It can be used to generate quite professional looking plots. There is a lot of information on the internet about calling Fortran from Python, but what if all you want to do is generate some plots from your (modern) Fortran program? With this in mind, I've created a very simple Fortran wrapper for Pyplot, allowing you to make pretty good plots by writing only Fortran code. Consider the following example:
program test
use,intrinsic :: iso_fortran_env, only: wp => real64
use pyplot_module
implicit none
real(wp),dimension(100) :: x,sx,cx,tx
type(pyplot) :: plt
integer :: i
!generate some data:
x = [(real(i,wp), i=0,size(x)-1)]/5.0_wp
sx = sin(x)
cx = cos(x)
tx = sx * cx
!plot it:
call plt%initialize(grid=.true.,xlabel='angle (rad)',&
title='python_plot test',legend=.true.)
call plt%add_plot(x,sx,label='\$\sin (x)\$',&
linestyle='b-o',markersize=5,linewidth=2)
call plt%add_plot(x,cx,label='\$\cos (x)\$',&
linestyle='r-o',markersize=5,linewidth=2)
call plt%add_plot(x,tx,label='\$\sin (x) \cos (x)\$',&
linestyle='g-o',markersize=2,linewidth=1)
call plt%savefig('test.png')
end program test
The main user interface is the pyplot class, which has methods such as initialize, add_plot, and savefig. This example produces the following plot:
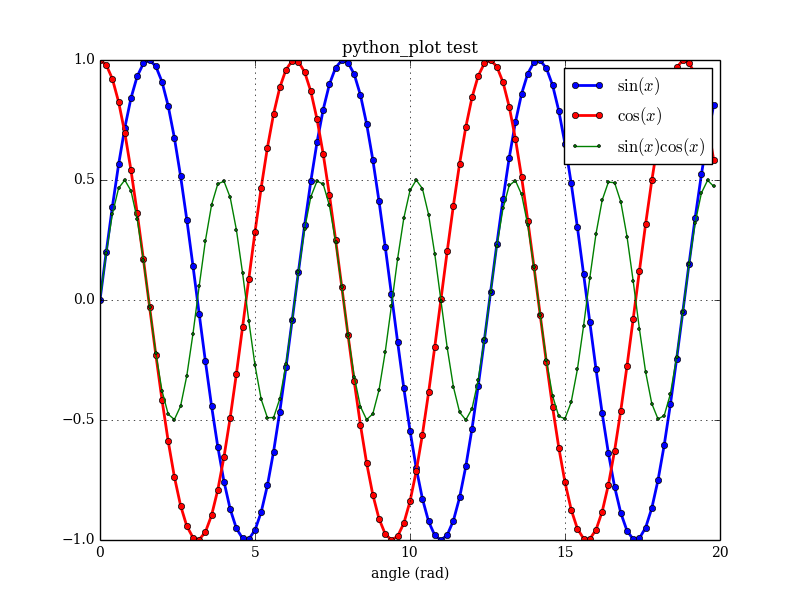
All the module does is generate a Python script, and then runs it and saves the result. The Python call is completely transparent to the Fortran user.
I posted the project to GitHub (pyplot-fortran). Maybe someone else will find it useful, or help to expand it.
A simple Fortran implementation of interpolation by Lagrange polynomials is given below. Though named after Joseph-Louis Lagrange, the formula was first discovered by English mathematician Edward Waring.
subroutine lagrange_interpolation(xx,yy,x,y)
!
! Interpolate xx=[x1,x2,...xn]
! yy=[f(x1),f(x2),...,f(xn)]
! Using Lagrange polynomial P(x)
! Returns y = P(x)
!
use,intrinsic :: iso_fortran_env, wp => real64
implicit none
real(wp),dimension(:),intent(in) :: xx
real(wp),dimension(:),intent(in) :: yy
real(wp),intent(in) :: x
real(wp),intent(out) :: y
!local variables:
integer :: j,k,n,m
real(wp) :: p
!check number of points:
n = size(xx)
m = size(yy)
if (n/=m) error stop &
'Error: vectors must be the same size.'
!sum each of the Pj(x) terms:
y = 0.0_wp
do j=1,n
!compute Pj(x):
p = yy(j)
do k=1,n
if (k/=j) p = p * (x-xx(k)) / (xx(j)-xx(k))
end do
y = y + p
end do
end subroutine lagrange_interpolation
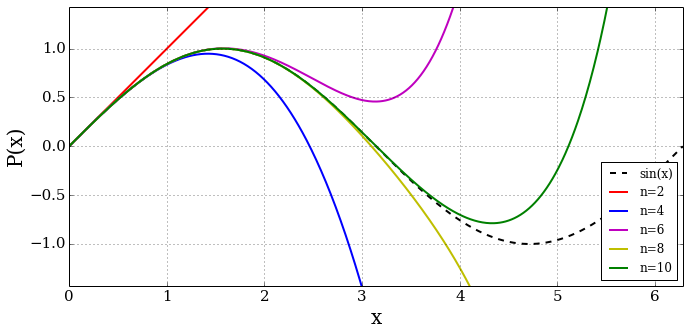
Examples of interpolating polynomials for the \(\sin(x)\) function are shown here for different numbers of points \(x=[0.0, 0.01]\), \(x=[0.0, 0.01, 0.02]\), etc.
There is a lot of confusion and misinformation about the Fortran programming language on the internet, and a general ignorance about it among programmers. Most younger programmers who use languages invented five minutes ago probably have never seen it, and may only be dimly aware of it as some obsolete language that nobody uses anymore.
You may be surprised to learn that Fortran is a modern, object-oriented, general-purpose programming language. Fortran is not a programming language created by computer scientists to write operating systems, nor does it include every single programming concept anyone's ever heard of. It is a language designed for computational efficiency and efficient array manipulation, and has a clear uncluttered syntax that can be read and understood by non-experts with only a little effort and training. It is particularly suited for numerical and scientific programming by non-expert programmers such as engineers and scientists. Learning all of Fortran is considerably easier than learning all of C++ (as an example). Sure, you can't do template metaprogramming, but few engineer/scientist types would ever want to do that anyway (besides, it's bad for you and could make you go blind).
By "Fortran", I mean modern Fortran (i.e., Fortran 2003 and 2008, which is the latest standard). Yes, the roots of Fortran go way back to the 1950s. Sure, early Fortran programs were written on punched cards. So what? Latin was once scratched into wax tablets, but that isn't really relevant to modern Italian and French speakers. In fact, the Fortran language has evolved considerably since it was first standardized in 1966. It generally has followed a cycle where a major update is followed by a minor update (1977=minor, 1990=major, 1995=minor, 2003=major, 2008=minor). It has been said that the 2003 update was as big an update to Fortran 95 as C++ was to C! Ten years later, the GNU Fortran compiler is still not fully F2003 compliment (the Intel compiler only recently became so).
People who attempt to enter the world of Fortran programming are easily corrupted and discouraged by misinformation. Even a lot of old-school Fortran users are unaware of the later standards. This is too bad, because modern Fortran is actually quite a respectable programming language for a lot of technical applications. This article is a pretty good overview of Fortran for C/C++ programmers. However, it is outdated, since it is confined to Fortran 95. Most of the limitations it mentions (no procedure pointers, clunky character strings, lack of an intent attribute for pointer dummy arguments, the nonstandardness of the ; character) have been rectified in subsequent standards.
The fact is the internet is not really the best source of information for modern Fortran. One day, maybe, there will be vibrant community of Fortran users on the internet, extensive online documentation, open source projects, and all your questions will simply be a web search away (cf., Python). But for now, you'll probably have to buy some books. If a book has the numbers 77, 90, or 95 in the title, don't open it, it will only confuse you. This is not to say that there aren't friendly Fortran folk on the internet who will also help you out. Two of the best places to go with questions are the Intel Fortran forum and the comp.lang.fortran newsgroup (yes, apparently, Usenet still exists).